Dr. Lalitha Subramanian
About the Author

Aksharam
A relation between two sets $X$ and $Y$ is a correspondence between elements of set $X$ and the elements of set $Y$. This can also be defined as a set of points in a $xy$- plane, whose coordinates are $(x,y)$ such that $x \in X$ and $y \in Y$.
A function is a relationship or mapping of the elements of a set $X$ to the elements of a set $Y$ such that each element in the set $X$ is mapped to a unique element in the set $Y$, by a rule.
The elements of the set $X$ are called input values and the elements of the set $Y$ which correspond to any element of the set $X$ are called the output values.
The set $X$ is called the Domain and the the set $Y$ is called the Codomain. The set of all elments of $Y$ that correspond to any element of $X$ is called the Range. Obviously, Range is a subset of Codomain.
All relations are not functions. Only the relations which map each input value to a unique output value are functions.
A function can also be viewed as a Rule that produces a unique element in the set of $Y$ for every element in the set of $X$, the elements of the set $Y$ is dependent on the elements of $X$. So, if we represent the elements of $Y$ as $y$, and the elements of $X$ as $x$, $x$ is called the independent variable and $y$ is called the dependent variable.
A relationship between two sets $X$ and $Y$ can be represented by any of the following ways:
Diagramatic representation: In the following diagram, Figure(a) has more than one element of $X$ mapped to an element of $Y$. But this mapping conforms to the rule of a function. This type of function is called Many-to-one function. Figure(b) has each element mapped to exactly one element in $Y$. This relationship also conforms the rule of a function. This type of function is called One-to-one function. Figure(c) has at least one element of $X$ mapped to more than one element of $Y$. This does not conform to the rule of a function. So, these types of one-to-many relationships are not functions .

Determine the type of relationship represented in the following diagram and state whether it is function or not:
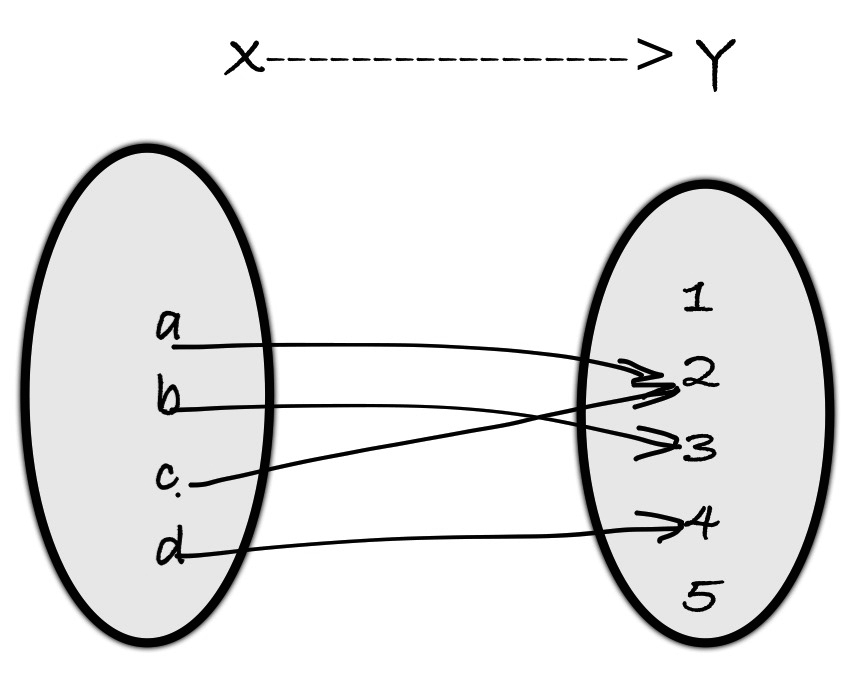
Solution: As more than one element of $X$ is mapped to one element of $Y$, this is s many-to-one function. Note that the domain of the function is the set $\{a,b,c,d\}$ and the range is $\{2,3,4\}$ while the codomain is $\{1,2,3,4,5\}$.
Algrbraic representation: The rule that associates the variable $x$ to the variable $y$ is written as $y = f(x)$,and read as "$y$ is a function of $x$.", or "$y$ is the value of $f$ at $x$. We can determine if a rule defines a function or not by checking if any value of $x$ gives more than one value for $y$ according to that rule.
Determine whether the formula $y=x^2-2x+5$ defines a function.
Solution: Yes. Because, when we plug in any value for $x$ in the formula, we get a unique value of $y$. As any value of $x$ plugged into the equation gives a unique real value of $y$, the domain of this function is the set of all real numbers $(-\infty, \infty)$ and the range is also the set of all real numbers $(-\infty, \infty)$
Determine if the formula $x^2+y^2-2x=6$ defines a function.
Solution: No. Solving this formula for $y$, we get \begin{eqnarray} y^2 &=& 6-x^2+2x\\ y &=& \pm \sqrt{6-x^2+2x}\\ \end{eqnarray} This means, for each value of $x$ we substitute in the formula, we get two values of $y$. So, this is not a function.
Graphical representation: Any relationship between $x$ and $y$ can be graphed by plotting ordered pairs $(x,y)$ that satisfy the relationship. A graph defines a function if and only if no vertical line intersects the graph in more than one point. If a vertical line intersects the graph in more than one point, this would mean that the graph gives more than one value for $y$ for that particular value of $x$ where that vertical line is placed. This test of determining a funtion using graph is called vertical line test .
Below are two graphs that confirm this rule.

In the above graph, the vertical line intersects the graph in two points. So, this is not the graph of a function.

The above graph is a function a vertical line crosses the graph in exactly one point. Note that this is true for any vertical line.
Set representation: A relation can be represented by a set of ordered pairs $(x,y)$ where the values of $x$ are in the domain and the values of $y$ are in the range. In this representation, we just need to check if any value of $x$ is paired with more than one value of $y$.
Check whether or not the set of ordered pairs $\{(1,2), (2,4), (5,1),(1,8)\}$ defines a funciton.
Solution: No. Note that $x=1$ is paired with $y=2$ and $y=8$.
Determine if the set $\{(4,1), (3,8), (1,2), (5,2)\}$ defines a function.
Solution: Yes. Note that each velue of $x$ is paired with a different value of $y$. Also note that the values $x=1$ and $x=5$ are paired with the value of $y=2$. This is a many-to-one function. Domain of this function is ${1,3,4,5}$ and range is ${1,2,8}$.
The domain of a function is the set of all values of $x$ that makes the value of the function meaningful. Unless otherwise stated or implied, domain of all polynomial functions is the set of real numbers $(-\infty,\infty)$.
The domain of a rational function is the set of all real numbers that do not make the demominator expression zero.
The domain of a radical function is the set of all realnumbers that make a non-negative radicand. Range of a function is the set of all values of $y$ that correspond to the values of $x$.
Find the domain and range of the function $y=\sqrt{x-2}$
Solution: To find the domain, set the radicand greater than or equal to zero, and solve. \begin{eqnarray} x-2 &\geq& 0\\ x &\geq& 2\\ \end{eqnarray} So, the domain of this function is $\{x|x \in \mathcal{R} : x \geq 2\}$
In interval notation, domain is $[2,\infty)$. The least value of $x$ is 2, which result in $y=0$. All values of $y$ are positive. So, the range of this function is $\{y| y \in \mathcal{R}: y \geq 0\}$. In interval notation, range is $[0, \infty)$.
Find the domain and range of the function $y=\frac{x+2}{x-3}$.
Solution: To find the domain, set the denominator to zero, and solve.Then, exclude thls value from the set of real numbers.
\begin{eqnarray} x-3 &=& 0\\ x &=& 3\\ \end{eqnarray}
So the domain is $\{x| x \in \mathcal{R}:x \neq 0\}$ and in interval notation, $(-\infty,0) \cup (0, \infty)$
Range is the set all real numbers $(-\infty, \infty)$
Find the domain and range of the function $f(x)=\frac{2x-3}{\sqrt{x+1}}$
Solution: Domain: While numerator can take all values, denominator cannot be zero, and cannot be negative because of the square-root. So, the domain would be all real numbers that satisfies the inequality $x+1 \gt 0$. Solving this would result in all values of $x \gt -1$. So, domain of this function is $\{x | x \in \mathcal{R} : x \gt -1\}$ in set notation and $(-1, \infty)$ in interval notation. Range: As the denominator is always positive and can be either less than or more than $1$, the range is all real numbers $\{x|x\in \mathcal{R}\}$ in set notation and $(-\infty,\infty)$ in interval notation.
As the algebraic notation of a function $y = f(x)$ suggests, the variable $x$ is the input value of the function. The value of the function is the output value $y$, which is the result of substituting the value of $x$ in the expression f(x).
Find the value of the function $y=x^2-3$ for $x=-2$.
Solution: Substituting the $x=-2$ in the function, we get \begin{eqnarray} y &=& (-2)^2-3\\ &=& 4-3\\ &=& 1\\ \end{eqnarray}
A function is defined by $f=\sqrt{1-2x}$. Find the point where the graph of this function intersects $x$-axis..
Solution: Any point on the $x$-axis has its $y$ coordinate $0$. So, the x- intercepts are obtained by solving $f(x)=0$. \begin{eqnarray} \sqrt{1-2x} &=& 0 \\ 1-2x &=& 0\\ 1 &=& 2x\\ \frac{1}{2} &=& x\\ \end{eqnarray}
A function is defined by the set of ordered pairs $f=\{(-2,3), (-1,0), (0,1), (1,0), (2,1)\}$. Find f(-1).
Solution: Note that the ordered pair that has $x$- coordinate $-1$ has $y$-coordinate $0$.So, $f(-1)=0$.
Yes. It is a many-to-one function.
No. It does not define a function because the element 3 from the set $X$ is mapped to two elements $a$ and $d$ in the set $Y$.