Dr. Lalitha Subramanian
About the Author

Aksharam
A quadratic equation in one variable is of the form $ax^2+bx+c=0$ where $a$, $b$,and $c$ are real numbers and $a\neq 0$.
To solve a quadratic equation means to find all values of $x$ for which the equation is true. As this is a second degree equation,
we have at most two values that would satisfy the equation. So, we call the pair of values as solution set.
To solve a quadratic equation $ax^2+bx+c=0$ also means to find the $x$-intercepts of the graph of $y=ax^2+bx+c$. The values of the solutions are also
called the roots or zeros of the equation.
Generally, a quadratic equation can be solved algebraically in any one of the following methods:
Solve the equation $x^2 - 3x +2=0$
Solution: Algebraically, we can factor the left side and set each factor to zero. Then solve each resulting linear equation to get the solution set. \begin{eqnarray} x^2-3x+2 &=& 0\\ (x-1)(x-2) &=& 0\\ x-1 &=& 0 &or& x-2 &=& 0\\ x &=& 1 &or& x &=& 2\\ \end{eqnarray}
So, solution set is {1,2}
Graphically, we can sketch the graph of the equation $y=x^2-3x+2$ and determine the $x$ intercepts of this graph.
Solve $(2x+1)^2=9$ by square roots method.
Solution: We solve it by taking square root on both sides: \begin{eqnarray} (2x+1)^2 &=& 9\\ 2x+1 &=& \pm 3\\ 2x+1 &=& 3 &or& \quad 2x+1 &=& -3\\ 2x &=& 2 &or& \quad 2x &=& -4 \\ x &=& 1 &or&\quad x &=& -2\\ \end{eqnarray}
Solve $3(2x-1)^2-4=0$ by square roots method.
Solution: We do this by rewriting the equation in the form $(X)^2=A$ where $(X)$ is an expression in $x$ and $A$ is a constant. Then, we solve it by taking square root on both sides, like the previous problem. \begin{eqnarray} 3(2x-1)^2-4 &=& 0\\ 3(2x-1)^2 &=& 4\\ (2x-1)^2 &=& \frac{4}{3}\\ 2x-1 &=& \pm \sqrt{\frac{4}{3}}\\ 2x-1 &=& \frac{2}{\sqrt{3}} &or& \quad 2x-1 &=& -\frac{2}{\sqrt{3}}\\ 2x-1 &=& \frac{2\sqrt{3}}{3} &or& \quad 2x-1 &=& -\frac{2\sqrt{3}}{3}\\ 2x &=& 1+\frac{2\sqrt{3}}{3} &or& \quad 2x &=& 1-\frac{2\sqrt{3}}{3}\\ x &=& \frac{1}{2}+\frac{\sqrt{3}}{3} &or& \quad x &=& \frac{1}{2}-\frac{\sqrt{3}}{3}\\ \end{eqnarray}
Solve $x^2+6x-7=0$ by completing the square method.
Solution: \begin{eqnarray} x^2+6x-7 &=& 0\\ \end{eqnarray}
Take the constant term to the right side:\begin{eqnarray} x^2+6x &=& 7\\ \end{eqnarray}
Complete the square: \begin{eqnarray} x^2+6x+3^2 &=& 7+3^2\\ (x+3)^2 &=& 16\\ \end{eqnarray}
Now we can solve this by taking square root on both sides: \begin{eqnarray} x+3 &=& \pm 4\\ x+3 &=& 4 &or& \quad x+3 &=& -4\\
x &=& 1 &or& \quad x &=& -7\\ \end{eqnarray}
Solve $2x^2-7x+9=(x-3)(x+1)+3x$ by completing the square method.
Solution: Rewrite the equation by simplifying the right side: \begin{eqnarray} 2x^2-7x+9 &=& x^2-2x-3+3x\\ 2x^2-7x+9 &=& x^2+x-3\\ \end{eqnarray}
Take all terms containing the variable to the left side, all constant terms to the right side, and simplify:
\begin{eqnarray} 2x^2-x^2-7x-x &=& -3-9\\ x^2-8x &=& -12\\ \end{eqnarray}
Complete the square: \begin{eqnarray} x^2-8x+4^2 &=& -12+4^2\\ (x-4)^2 &=& 4\\ \end{eqnarray}
Take square root on both sides and solve for $x$: \begin{eqnarray} x-4 &=& \pm 2\\ x-4 &=& 2 &or& \quad x-4 &=& -2\\ x &=& 6 &or& \quad x &=& 2\\
\end{eqnarray}
Solve $2x^2+4x+52=0$ by completing the square method.
Solution:
Step 1: Take the constant term to the right side: \begin{eqnarray} 2x^2+4x &=& -52\\ \end{eqnarray}
Step 2: Divide both sides by 2 in order to make the coefficient of $x^2=1$: \begin{eqnarray} x^2+2x &=& -26\\ \end{eqnarray}
Step 3: Complete the square: \begin{eqnarray} x^2+2x+1 &=& -25\\ (x+1)^2 &=& -25\\ \end{eqnarray}
Step 4: Take square root on both sides and solve for $x$: \begin{eqnarray} x+1 &=& \pm 5i\\ x &=& -1+5i &or& \quad x &=& -1-5i\\
\end{eqnarray}
Solve $2x^2-3x+1=0$ by using the quadratic formula.
Solution: Here, $a=2$, $b=-3$, and $c=1$. Substitute these values in the quadratic formula and simplify: \begin{eqnarray} x &=& \frac{-(-3) \pm \sqrt{(-3)^2-4(2)(1)}}{2(2)}\\ x &=& \frac{3 \pm \sqrt{9-8}}{4}\\ x &=& \frac{3 \pm 1}{4}\\ x &=& \frac{4}{4} &or& \quad x &=& \frac{2}{4}\\ x &=& 1 &or& \quad x &=& \frac{1}{2}\\ \end{eqnarray}
Solve $x^2+4x-6=0$ by using the quadratic formula.
Solution: Here, $a=1$, $b=4$, and $c=-6$. Substitute these values in the quadratic formula and simplify: \begin{eqnarray} x &=& \frac{-(4) \pm \sqrt{(4)^2-4(1)(-6)}}{2(1)}\\ x &=& \frac{-4 \pm \sqrt{16+24}}{2}\\ x &=& \frac{-4 \pm 2\sqrt{10}}{2}\\ x &=& -2 +\sqrt{10} &or& x &=& -2-\sqrt{10}\\ \end{eqnarray}
The quadratic formula for solving the equation $ax^2+bx+c=0$ is $\frac{-b \pm \sqrt{b^2-4ac}}{2a}$. In this formula, the radicand $\sqrt{b^2-4ac}$ is called the discriminant because it helps us to discriminate the nature of roots of the equations.
Determine the nature of zeros of the equation $x^2+2x+5$ without actually solving it.
Solution: Here, $a=1$, $b=2$, and $c=5$. So,the discriminant is: \begin{eqnarray} 2^2-4(1)(5) &=& 4-20\\ &=& -16 &\lt&0\\ \end{eqnarray}
So,this equation has a complex conjugate pair of roots. No real roots implies that the graph does not intersect $x$-axis.
Solve: $3x^2+x+2=0$
Solution: Substitute $a=3$, $b=1$, and $c=2$ in the quadratic formula and simplify: \begin{eqnarray} x &=& \frac{-1 \pm \sqrt{1^2-4(3)(2)}}{2(3)}\\ x &=& \frac{-1 \pm \sqrt{-23}}{6}\\ x &=& \frac{-1+i\sqrt{23}}{6} &or& \quad x &=& \frac{-1-i\sqrt{23}}{6}\\ x &=& -\frac{1}{6} + \frac{i\sqrt{23}}{6} &or& -\frac{1}{6} - \frac{i\sqrt{23}}{6}\\ \end{eqnarray}
Solve problems #1 - #6 by factoring:
$\{3,5\}$
$\{-3,\frac{1}{2}\}$
$\{-\frac{1}{2},1\}$
$\{-3,1\}$
$\{\frac{2}{5}, \frac{2}{3}\}$
Solve problems #7 - #12 by taking square root on both sides:
$\{0,8\}$
$\{ -\frac{5}{2}, \frac{1}{2}\}$
$\{\frac{1}{5},3\}$
$\{-\frac{4}{3}-\frac{\sqrt{6}}{3}, -\frac{4}{3}+\frac{\sqrt{6}}{3}\}$
$\{3-i\sqrt{5}, 3+i\sqrt{5}\}$
Solve problems #13 - #16 by completing the square method:
$\{1 - \frac{\sqrt{14}}{2}, 1+\frac{\sqrt{14}}{2}\} $
$\{3-2\sqrt{3}, 3+2\sqrt{3}\}$
$\{2-\sqrt{2}, 2+\sqrt{2}\}$
Solve problems #17-22 using the quadratic formula
$\{1-\frac{2\sqrt{6}}{3}, 1+\frac{2\sqrt{6}}{3}\}$
$\{-4,8\}$
$\{ 1-i, 1+i\}$
$\{\frac{-1}{6}-\frac{\sqrt{13}}{6}, \frac{-1}{6}+\frac{\sqrt{13}}{6}\}$
$\{\frac{3}{5}-i\frac{\sqrt{6}}{5}, \frac{3}{5}+i\frac{\sqrt{6}}{5}\}$
No Solution
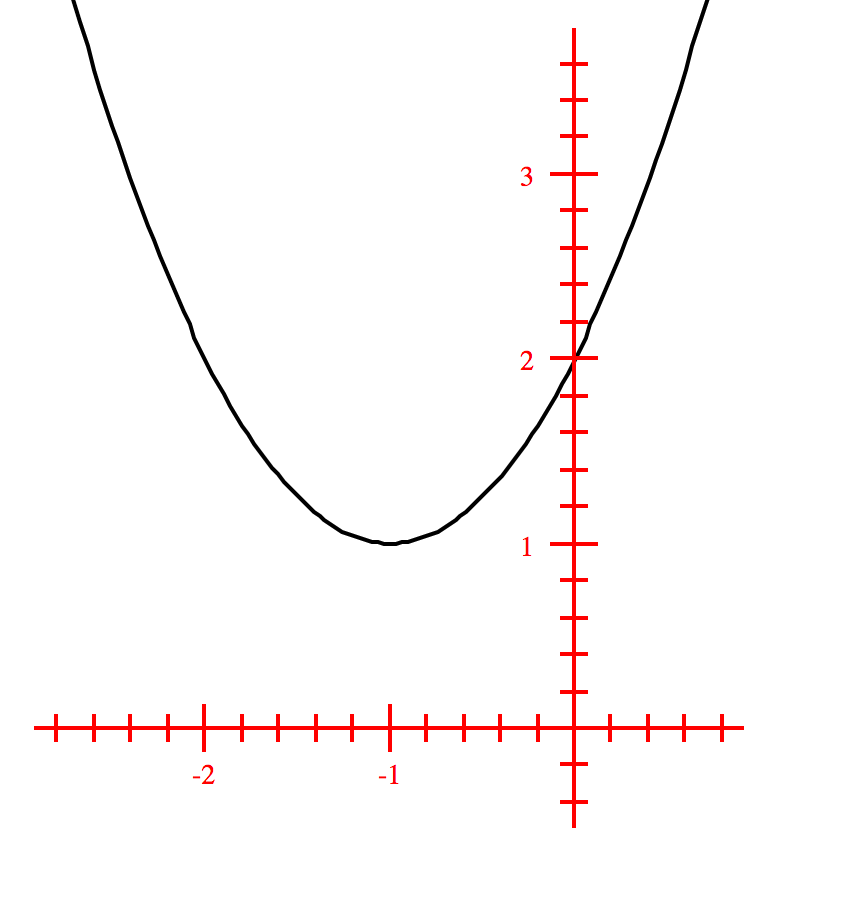
Two distinct real roots.
One real root