Precalculus

Dr. Lalitha Subramanian
About the Author

Aksharam

Chapter P - Preliminary Concepts

P4: LINES IN A PLANE

Given two points P($x_1, y_1)$ and Q$(x_2, y_2)$, distance between P and Q is given by the formula $$d=\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$$

Example 1:

Find the distance between the points (1, 5) and (6, - 2)

Solution: \begin{eqnarray} d &=& \sqrt{(1-6)^2 + (5-(-2))^2}\\ &=& \sqrt{(-5)^2 + (7)^2}\\ &=& \sqrt{25+49}\\ &=& \sqrt{79}\\ &=& 8.89\\ \end{eqnarray}

Coordinates of the mid point of the line segment PQ is given by the formula $$\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$$

Example 2:

Find the coordinates of the midpoint of the line segment joining P(-5, 2) and Q(3, 7).

Solution: \begin{eqnarray} (x, y) &=& \left(\frac{-5+3}{2}, \frac{2+7}{2}\right)\\ &=& (-1, 4.5)\\ \end{eqnarray}

The SLOPE of a line through the points P$(x_1, y_1)$ and Q$(x_2, y_2)$ is given by the formula: $$m = \frac{y_2 - y_1}{x_2 - x_1}$$.

Example 3:

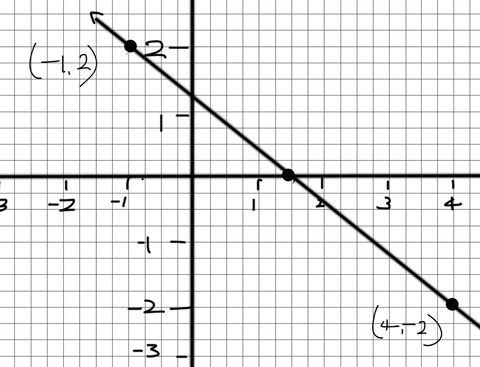
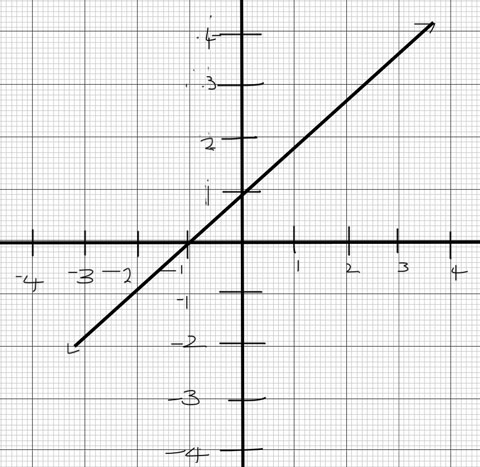
Find the slope of the line through the points P(-1, 2) and Q(4, -2) and sketch the line.

Solution: \begin{eqnarray} m &=& \frac{(-2)-2}{4-(-1)}\\ &=& -\frac{4}{5}\\ \end{eqnarray}

An equation of a graph is an equation in two variables $x$ and $y$, where $x$ and $y$ represent the $x$ and $y$ coordinates of any point on that graph. There is a one-one relationship between the coordinates of any point on the graph and the ordered pairs $(x,y)$ that satisfy the equation. That is, coordinates of any point on the line should satisfy the equation of the line and any order pair of numbers $(x,y)$ that satisfies the equation should represent a point on the graph.
A linear equation in $x$ and $y$ always represents the graph of a line.

DIFFERENT FORMS OF EQUATIONS OF A LINE

Graphing a line is easier if we remember the basic property of the line: "Two distinct points determine a unique line."

So, if we can find two distinct points satisfying a given equation, we can join them and extend on both sides to get the graph of the line. Alternately if we know the slope and $y$- intercept of a line, we can use the fact that $slope = \frac{rise}{run}$ and graph the line.

Example 4:

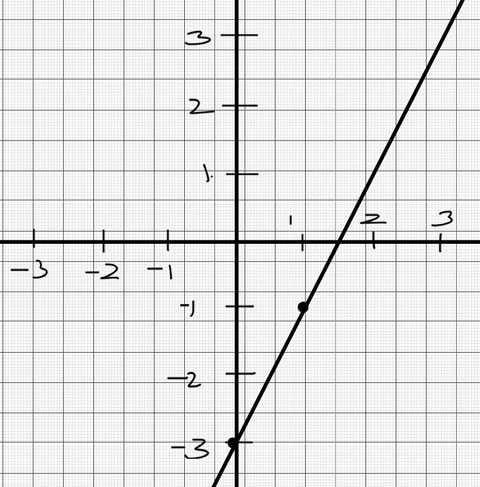
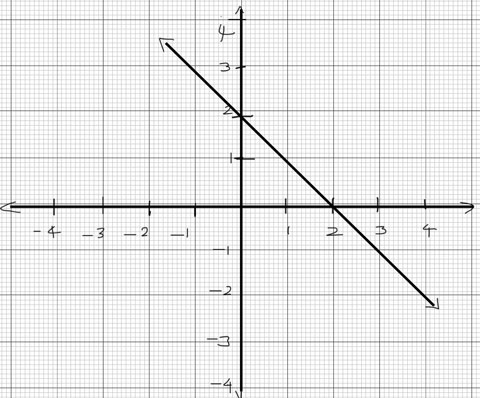
Graph the line $y=2x-3$

Solution: This equation is given in slope-intercept form. Slope of the line is $2$ and y-intercept is $-3$. We can fix the first point on the y-axis as $(0, -3)$ to show the y- intercept. To get the second point, we use the definition of slope as $\frac{rise}{run}$. Here, slope is $2 = \frac{2}{1}$. That is, from the point $(0, -3)$, go up vertically by $2$ units (rise) and horizontally $1$ by unit (run), to get the second point $(1,-1)$.

Alternately, we can graph the line by getting the two intercepts. The y- intercept is obtained by setting $x=0$ in the equation and solving for $y$. We can get the x- intercept by substituting y = 0 in the equation and solving for x. Remember that all points on the x- axis have y-coordinate zero. Similarly all points on the y- axis have their x-coordinates zero.

We can graph a line whose equation is given in any of the above mentioned form, by just algebraically transforming it into slope-intercept form.

Example 5:

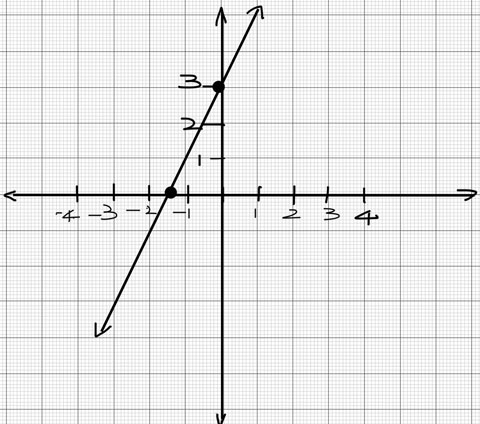
Graph the line $y-5=2(x-1)$

Solution: This equation is in point-slope form. First let us bring it to slope-intercept form:

\begin{eqnarray} y-5 &=& 2x-2\\ y &=& 2x+3\\ \end{eqnarray}

Now, we can graph this line following any one of the two methods shown in Example 1.
Alternately, we can take the first point as the given point $(1,5)$ and take the slope of $2$ to get the second point.

Example 6:

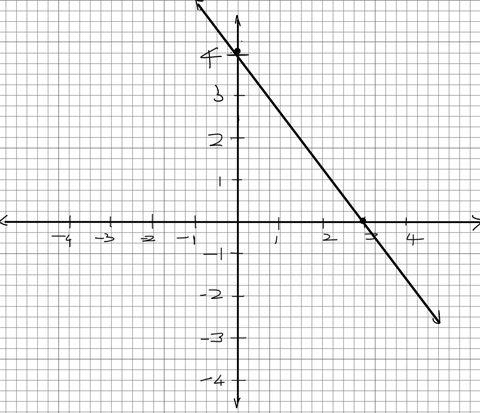
Graph the line $\frac{x}{3} + \frac{y}{4}=1$

Solution: This equation is in two-intercepts form. So, the easiest way to graph this line is to plot the two intercepts

We note that the $x$- intercept is $(3, 0)$ and the $y$- intercept is $(0, 4)$.

Example 7:

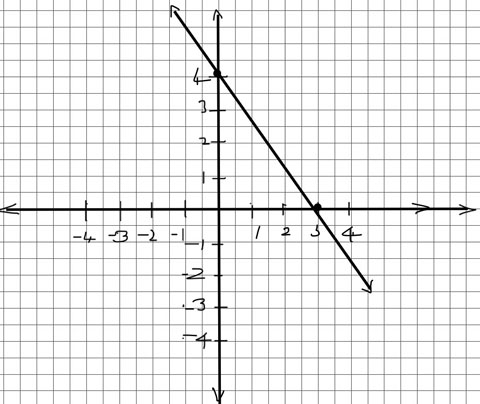
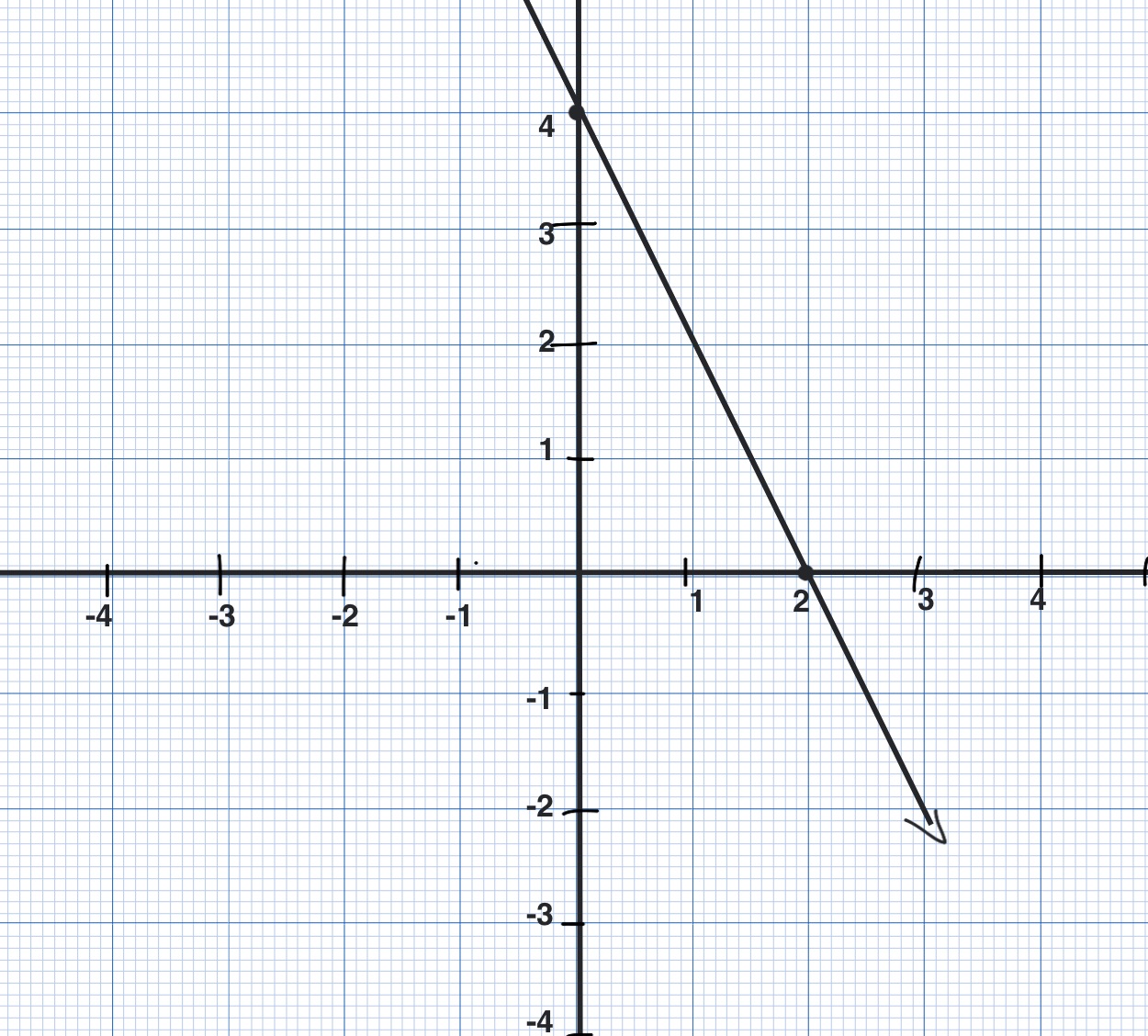
Graph the line $4x + 3y = 12$.

Solution: This equation is in general form. We can bring this into slope-intercept form and then graph the line using any one of the methods stated in Example 2. \begin{eqnarray} 3y &=& -4x+12\\ y &=& -\frac{4}{3}x + 4\\ \end{eqnarray}

So slope of this line is $-\frac{4}{3}$ and y-intercept is $4$.

Following points are to be noted when working on problems involving lines and graphs:

If two lines $y = m_1 x + c_1$ and $y=m_2 x + c_2$ are parallel, then their slopes are equal. That is, $m_1=m_2$. Conversely, if slopes of two lines are equal, these lines are parallel.

If two lines $y = m_1 x + c_1$ and $y=m_2 x + c_2$ are perpendicular, then their slopes are negative reciprocal of each other.

Conversely, if slopes of two lines are negative reciprocals of each other, then these lines perpendicular.

Example 8:

Determine the equation of a line parallel to the line $y=2x+3$ that contains the points $(-1,4)$.

Solution:
Equation of the given line is in slope- intercept form. So, its slope = 2.
Any line parallel to this line also has slope = 2.
Equation of the required line in point-slope form is \begin{eqnarray} y-4 &=& 2(x+1)\\ y-4 &=& 2x+2\\ y &=& 2x+6\\ \end{eqnarray}

Example 9:

Find the equation of the line perpendicular to the line $3x-4y=8$ passing through $(3, -1)$.

Solution: Given line is in general form. So, we need to bring this into slope- intercept form first. \begin{eqnarray} 3x-4y &=& 8\\ -4y &=& -3x+8\\ y &=& \frac{3}{4}x+2\\ \end{eqnarray}

Slope of the given line is $\frac{3}{4}$.
So, slope of a perpendicular line is $-\frac{4}{3}$.
Equation of the required line in point-slope form \begin{eqnarray} y+1 &=& -\frac{4}{3}(x-3)\\ y+1 &=& -\frac{4}{3}x + 4\\ y &=& -\frac{4}{3}x+3\\ \end{eqnarray}

This is in slope-intercept form. We can write this in general form as follows: \begin{eqnarray} y &=& -\frac{4}{3}x+3\\ 3y &=& -4x+9\\ 4x+3y &=& 9\\ \end{eqnarray}

Example 10:

Determine the equation of a line through a point A $(-2,3)$ that is perpendicular to the line whose equation is $2x+y=5$.

Solution:
Equation of the given line: $2x+y=5$
Rewrite this in slope-intercept form: \begin{eqnarray} y &=& -2x+5\\ \end{eqnarray}

Slope of the given line is -2.
Slope of any line perpendicular to this line is $\frac{1}{2}$
The required line passes through A $(2, -3)$.
Equation of the required line in point-slope form is \begin{eqnarray} y+3 &=& \frac{1}{2}(x-2)\\ \end{eqnarray}

Simplifying and writing the equation in general form: \begin{eqnarray} 2y+6 &=& x-2\\ 2y-x &=& -8\\ x-2y &=& 8\\ \end{eqnarray}

Example 11:

Find the equation, in general form, of a line through the point $(-5,4)$ which is perpendicular to the line $3x-4y=7$

Solution: Equation of the given line in slope-intercept form: \begin{eqnarray} 4y &=& 3x-7\\ y &=& \frac{3}{4}x-\frac{7}{4}\\ \end{eqnarray}
Slope of the given line is $\frac{3}{4}$. So, slope of any line perpendicular to this line is $-\frac{4}{3}$.
This required line passes through the point $(-5,4)$. So, the required equation in point-slope form: \begin{eqnarray} y-4 &=& -\frac{4}{3}(x+4) \end{eqnarray}
General form of the equation: \begin{eqnarray} 3y-12 &=& -4x-12\\ 4x+3y &=& 0\\ \end{eqnarray}