Solve each of the following equations by factorization: $(a) 2x^2 + 15x + 27 = 0; \quad (b) x^2 + 4x - 12 = 0; \quad (c) y^2 - 16y - 80 = 0; \quad (d) 8x^2 - 18x + 9 = 0$

Solution:

$(a)$ To factorize this equation, recall that we first need to find the two factors of $P = 2 \times 27 = 54$ such that the sum of the factors equals the coefficient of the middle term $15$. Such a pair of factors is $6$ and $9$ as $6 \times 9 = 54$ and $6 + 9 = 15$. Factoring and solving this equation: \begin{eqnarray} 2x^2 + 15x + 27 &=& 0\\ 2x^2 + 6x + 9x + 27 &=& 0\\ 2x(x + 3) + 9(x + 3) &=& 0\\ (x + 3)(2x + 9) &=& 0\\ x + 3 &=& 0 \implies x = - 3\\ 2x + 9 &=& 0 \implies x = -\frac{9}{2}\\ \end{eqnarray}
So, the solution set is $\{-\frac{9}{2}, - 3\}$

$(b)$ Here, product $P = - 12$ and sum $ S = + 4$. Such a pair of factors are $+6$ and $-2$.: \begin{eqnarray} x^2 + 4x - 12 &=& 0\\ x^2 + 6x - 2x - 12 &=& 0 \\ x(x + 6) - 2(x + 6) &=& 0\\ ( x + 6)(x - 2) &=& 0\\ x + 6 &=& 0 \implies x= - 6\\ x - 2 &=& 0 \implies x = 2\\ \end{eqnarray}
So, solution set is $\{-6, 2\}$

$(c)$ In this equation, product of factors $P = -80$ and their sum $s = - 16$. Such a pair of factors are $-20$ and $4$: \begin{eqnarray} y^2 - 16y - 80 &=& 0\\ y^2 - 20y + 4y - 80 &=& 0\\ y(y - 20) + 4(y - 20) &=& 0\\ (y - 20)(y + 4) &=& 0\\ y - 20 &=& 0 \implies y = 20\\ y + 4 &=& 0 \implies y = - 4\\ \end{eqnarray}
So, solution set is $\{-4, 20\}$

$(d)$ For this equation, product is $P = 8 \times 9 = 72$ and sum $ s = - 18$. Such a pair of factors are $-12$ and $-6$: \begin{eqnarray} 8x^2 - 18x + 9 &=& 0\\ 8x^2 - 12x - 6x + 9 &=& 0\\ 4x(2x - 3) - 3(2x - 3) &=& 0\\ (2x - 3)(4x - 3) &=& 0\\ 2x - 3 &=& 0 \implies x = \frac{3}{2}\\ 4x - 3 &=& 0 \implies x = \frac{3}{4}\\ \end{eqnarray}
So, solution set is $\{\frac{3}{3}. \frac{3}{2}\}$

Solve each of the following equations by taking square root on both sides:
$(a) x^2 - 16 = 0; \quad (b) (y - 3)^2 - 7 = 0; \quad (c) (2x - 3)^2 = 9; \quad (d) (x + 5)^2 = 49;

Solution:

$(a)$ First take the constant term to the right side, and the take square root on both sides: \begin{eqnarray}x^2 &=& 16\\ \sqrt{x^2} &=& \pm \sqrt{16}\\ x &=& \pm 4\\ x &=& 4\\x &=& - 4\\ \end{eqnarray}
So, solution set is $\{- 4, 4\}$

$(b)$ First we take the constant term to the right side and take square root on both sides: \begin{eqnarray} (y - 3)^2 &=& 7\\ \sqrt{(y - 3)^2} &=& \pm \sqrt{7}\\ y - 3 &=& \pm \sqrt{7}\\ y - 3 &=& +\sqrt{7} \implies y = 3 + \sqrt{7}\\ y - 3 &=& -\sqrt{7} \implies y = 3 - \sqrt{7}\\ \end{eqnarray}
So, solution set is $\{3 + \sqrt{7}, 3 - \sqrt{7}\}$

$(c)$ We can directly start the process here: \begin{eqnarray} (2x - 3)^2 &=& 9\\ \sqrt{(2x - 3)^2} &=&\pm \sqrt{9}\\ 2x - 3 &=& \pm 3\\ 2x - 3 &=& 3 \implies x = 3\\ 2x - 3 &=& - 3 \implies x = 0\\ \end{eqnarray}
So, solution set is $\{0, 3\}$

$(d)$ We can directly start the process for this problem also: \begin{eqnarray} (x + 5)^2 &=& 49\\ \sqrt{(x + 5)^2} &=& \pm \sqrt{49}\\ x + 5 &=& \pm 7\\ x + 5 &=& 7 \implies x = 2\\ x + 5 &=& - 7 \implies x = - 12\\ \end{eqnarray}
So, solution set is $\{-12, 2\}$.

Solve each of the following equations by completing the square: $(a) x^2 - 6x - 3 = 0; \quad (b) y^2 - 4y + 2 = 0; \quad (c) 2t^2 + 4t + 1 = 0; \quad (d) 2n^2 - 8n - 3 = 0$

Solution:

$(a)$ First step is to take the constant term to the right side. Then, complete the square on the left side by adding appropriate third constant term, on both sides. After this step, the equation can be solved by taking square root on both side, like the previous method: \begin{eqnarray} x^2 - 6x - 3 &=& 0\\ x^2 - 6x &=& 3\\ x^2 - 6x + (3)^2 &=& 3 +9\\ (x - 3)^2 &=& 12\\ \sqrt{(x - 3)^2} &=& \pm \sqrt{12}\\ x - 3 &=& \pm 2 \sqrt{3}\\ x - 3 &=& + 2 \sqrt{3} \implies x = 3 + 2 \sqrt{3}\\ x - 3 &=& - 2 \sqrt{3} \implies x = 3 - 2 \sqrt{3}\\ \end{eqnarray} So, solution is $\{3 + 2 \sqrt{3}, 3 - 2 \sqrt{3}\}$

$(b)$ \begin{eqnarray} y^2 - 4y + 2 &=& 0\\ y^2 - 4y &=& - 2 \\ y^2 - 4y + (2)^2 &=& - 2 + (2)^2\\ (y - 2)^2 &=& 2\\ \sqrt{(y - 2)^2} &=& \pm \sqrt{2}\\ - 2 &=& \pm \sqrt{2}\\ y - 2 &=& + \sqrt{2} \implies y = 2 + \sqrt{2}\\ y - 2 &=& -\sqrt{2} \implies y = 2 - \sqrt{2}\\ \end{eqnarray} So, solution set is $\{2 + \sqrt{2}, 2 - \sqrt{2}\}$

$(c)$ First step is to take the constant term to the right side. In this problem, coefficient of the leading term $t^2$ term is not $1$. So, divide each term on both sides by this coefficient so that the $t^2$ term has unity coefficient. After this, proceed as in the previous problems: \begin{eqnarray} 2t^2 + 4t + 1 &=& 0\\ 2t^2 + 4t &=& - 1\\ t^2 + 2t &=& -\frac{1}{2}\\ t^2 + 2t + 1 &=& -\frac{1}{2} + 1\\ (t + 1)^2 &=& \frac{1}{2}\\ \sqrt{(t + 1)^2} &=& \pm \sqrt{\frac{1}{2}}\\ t + 1 &=& \pm \frac{\sqrt{2}}{2}\\ t + 1 &=& \frac{\sqrt{2}}{2} \implies t = - 1 + \frac{\sqrt{2}}{2}\\ t + 1 &=& - \frac{\sqrt{2}}{2} \implies t = - 1 - \frac{\sqrt{2}}{2}\\ \end{eqnarray} So, solution set is $\{ - 1 + \frac{\sqrt{2}}{2}, - 1 - \frac{\sqrt{2}}{2}\}$.

$(d)$ This equation is to be solved like the previous one: \begin{eqnarray} 2n^2 - 8n - 3 &=& 0\\ 2n^2 - 8n &=& 3\\ n^2 - 4n &=& \frac{3}{2}\\ n^2 - 4n + (2)^2 &=& \frac{3}{2} + 4\\ (n - 2)^2 &=& \frac{11}{2}\\ n - 2 &=& \pm \sqrt{\frac{11}{2}}\\ n - 2 &=& + \frac{\sqrt{11}}{2} \implies n = 2 + \frac{\sqrt{11}}{2}\\ n - 2 &=& - \frac{\sqrt{11}}{2} \implies n = 2 - \frac{\sqrt{11}}{2}\\ \end{eqnarray} So, solution set is $\{2 - \frac{\sqrt{11}}{2}, 2 + \frac{\sqrt{11}}{2}\}$

Find solution sets of each of the following quadratic equations using the quadratic formula: $(a) 2x^2 - 5x + 3 = 0; \quad (b) 4x^2 + 4\sqrt{3}x + 3 = 0; \quad (c) \frac{1}{x + 4} - \frac{1}{x - 7} = \frac{11}{30}, x \neq 4, 7; \quad (d) 2p^2 - 3p - 2 = 0$.

Solution:

$(a)$ In this equation, $a = 2, b = - 5, c = 3$. Substituting these values in the quadratic formula: \begin{eqnarray} x &=& \frac{5 \pm \sqrt{(-5)^2 - 4(2)(3)}}{2(2)}\\ &=& \frac{5 \pm \sqrt{25 - 24}}{4}\\ &=& \frac{5 \pm 1}{4}\\ x &=& \frac{5 + 1}{4} = \frac{6}{4} = \frac{3}{2}\\ x &=& \frac{5 - 1}{4} = 1\\ \end{eqnarray}. So, solution set is $\{1, \frac{3}{2}\}$

$(b)$ Here, $a=4, b=4\sqrt{3}, c=3$: \begin{eqnarray} x &=& \frac{-4 \pm \sqrt{(4\sqrt{3})^2 - 4(4)(3)}}{2(4)}\\ &=& \frac{-4 \pm \sqrt{48 - 48}}{8}\\ &=& \frac{- 4 \pm 0}{8}\\ &=& \frac{- 4}{8}\\ &=& - \frac{1}{2}\\ \end{eqnarray}. So, this equation has only one solution $x = -\frac{1}{2}$. We know that this means the graph of this equation touches the $x$-axis at $\left(\frac{1}{2}, 0\right)$.

$(c)$ This equation has fractions in each of the three terms. So, first we shall take LCM of the denominators and multiply each term on both sides by the LCM. LCM = $30(x + 4)(x - 7)$. Multiplying each term by this will give us $30(x - 7) - 30(x + 4) = 11(x + 4)(x - 7)$. We need to simplify and rearrange the terms in order to bring it in standard form before we can use the quadratic formula: \begin{eqnarray} 30(x - 7) - 30(x + 4) &=& 11(x + 4)(x - 7)\\ 30x - 210 - 30x - 120 &=& 11(x^2 - 3x - 28)\\ &=& 11x^2 - 33x - 308\\ - 330 &=& 11x^2 - 33x - 308\\ 0 &=& 11x^2 - 33x + 22\\ \end{eqnarray} From the standard form of the equation, we get $a = 11, b = - 33, c = 22$: \begin{eqnarray} x &=& \frac{33 \pm \sqrt{(-33)^2 - 4(11)(22)}}{2(11)}\\ &=& \frac{33 \pm \sqrt{1089 - 968}}{22}\\ &=& \frac{33 \pm \sqrt{121}}{22}\\ &=& \frac{33 \pm 11}{22}\\ x &=& \frac{33 + 11}{22} = 2\\ x &=& \frac{33 - 11}{22} = 1\\ \end{eqnarray} So, solution set is $\{1, 2\}$

$(d)$ Here, $a=2, b=-3, c=-2$: \begin{eqnarray} x &=& \frac{3 \pm \sqrt{(-3)^2 - 4(2)(-2)}}{2(2)}\\ &=& \frac{3 \pm \sqrt{9 + 16}}{4}\\ &=& \frac{3 \pm \sqrt{25}}{4}\\ &=& \frac{3 \pm 5}{4}\\ x &=& \frac{3 + 5}{4} = 2\\ x &=& \frac{3 - 5}{4} = \frac{-2}{4} = -\frac{1}{2}\\ \end{eqnarray} So, solution set is $\{-\frac{1}{2}, 2\}$.

Without solving each of the following equations, determine the nature of the roots: $(a) t^2 - 5t - 5 = 0; \quad (b) 3x^2 - 4x + 2 = 0; \quad (c) 4x^2 + 12x + 9 = 0$

Solution:

$(a)$ Substituting $a = 1, b = - 5, c = - 5$ in the discriminant, we get \begin{eqnarray} b^2 - 4ac &=& (- 5)^2 - 4(1)(- 5)\\ &=& 25 + 20\\ &=& 45\\ \end{eqnarray} As the discriminant is positive, this equation has two distinct real roots.
$(b)$ Substitutiong $a = 3, b = - 4, c = 2$ in the discriminant, we have \begin{eqnarray} b^2 - 4ac &=& (- 4)^2 - 4(3)(2)\\ &=& 16 - 24\\ &=& - 8\\ \end{eqnarray} As the discriminant is negative, this equation has no real roots.
$(c)$ Substituting $a = 4, b = 12 c = + 9$ in the discriminant, we have \begin{eqnarray} b^2 - 4ac &=& (12)^2 - 4(4)(9)\\ &=& 144 - 144\\ &=& 0\\ \end{eqnarray} As the discriminant is zero, this equation has one real root.

Find the values of the unknown constant $k$ in the equation $3x^2 - 6x - k = 0$ so that the equation has $(a)$ Two distinct real roots; $(b)$ One real root; $(c)$ No real roots.

Solution:

The discriminant for this equation is $$(-6)^2 - (4)(3)(-k) = 36 + 12k $$.
$(a)$ The equation will have two distinct real roots if the discriminant is positive: \begin{eqnarray} 36 + 12k &\gt& 0\\ 12k &\gt& - 36\\ k &\gt& -\frac{36}{12}\\ k &\gt& - 3\\ \end{eqnarray}. So, this equation will have two distinct real roots for $k \gt - 3$.
$(b)$ The equation will have one real root if the discriminant equals zero: \begin{eqnarray} 36 + 12k &=& 0\\ 12k &=& - 36\\ k &=& - 3\\ \end{eqnarray}. So, the equation will have one real root if $k = - 3$.
$(c)$ For this equation to have no real roots, the discriminant should be negative: \begin{eqnarray} 36 + 12k &\lt& 0\\ 12k &\lt& - 36\\ k &\lt& - 3\\ \end{eqnarray} So, this equation will have no real roots for any value of $k \lt - 3$.

Ram and Radha together have 45 marbles. Each of them gave away 5 marbles to their sisters respectively. NOw, the product of the marbles they have is 124. How many marbles did each have originally?

Solution:

Let the number of marbles Ram had originally be $x$. As they had 45 marbles together, number of marbles Radha had originally ls $45 - x$.
After they gave away 5 marbles each to their sisters, now, Ram has $x - 5$ marbles and Radha has $45 - x - 5 = 40 - x$ marbles. According to the given information, $(x - 5)(40 - x) = 124$. We can solve this equation after we first write it in standard form: \begin{eqnarray} (x - 5)(40 - x) &=& 124\\ 40x - x^2 - 200 + 5x &=& 124\\ - x^2 + 45x - 200 &=& 124\\ -x^2 + 45x - 324 &=& 0\\ x^2 - 45x + 320 &=& 0\\ (x - 36)(x - 9) &=& 0\\ x - 36 &=&= 0 \implies x = 36\\ x - 9 &=& 0 \implies x = 9\\ \end{eqnarray} Answer: One of them had 36 marbles and the other had 9 marbles originally.

Product of two consecutive even integers is 840. Find the two integers.

Solution:

We note that the difference between two even or two odd consecutive integers is 2. So, if one even integer is $x$, then the next consecutive even integer is $x + 2$. Given that the product of these two is 840. So, we have the equation $x(x + 2) = 840$ that models this situation. Rearranging the terms in standard form and solving: \begin{eqnarray} x(x + 2)&=& 840\\ x^2 + 2x &=& 840\\ x^2 + 2x - 840 &=& 0\\ (x - 28)(x - 30) &=& 0\\ x - 28 &=& 0 \implies x = 28\\ x - 30 &=& 0 \implies x = 30\\ \end{eqnarray}
Answer: The two even consecutive numbers are 28 and 30.

A train travels 360 km at a uniform speed.If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Solution:

For problems involving distance, speed, and time, we use the relation $t = \frac{d}{s}$ This problem can be easily modeled by making a table of the two situations: \begin{array}{aaa} distance(km) & speed(Km/h) & time(h)\\ \hline 360 & x & \frac{360}{x}\\ 360 & x + 5 & \frac{360}{x+5}\\ \end{array} According to the given information, with the increased speed, time taken reduces by 1 hour. That is, $$\frac{360}{x+5} = \frac{360}{x} - 1$$. We can multiply each term on both sides by the LCM $x(x+5)$ to eliminate the denominator and form a quadratic equation, the solution of which gives us the answer: \begin{eqnarray} 360(x) &=& 360(x + 5) - 1(x)(x + 5)\\ 360x &=& 360x + 1800 - x^2 - 5x\\ x^2 + 5x - 1800 &=& 0\\ (x + 45)(x - 40) &=& 0\\ x + 45 &=& 0 \implies x = - 45\\ x - 40 &=& 0 \implies x = 40\\ \end{eqnarray} We discard the negative value. So, the original speed of the train is $40$ km/h.

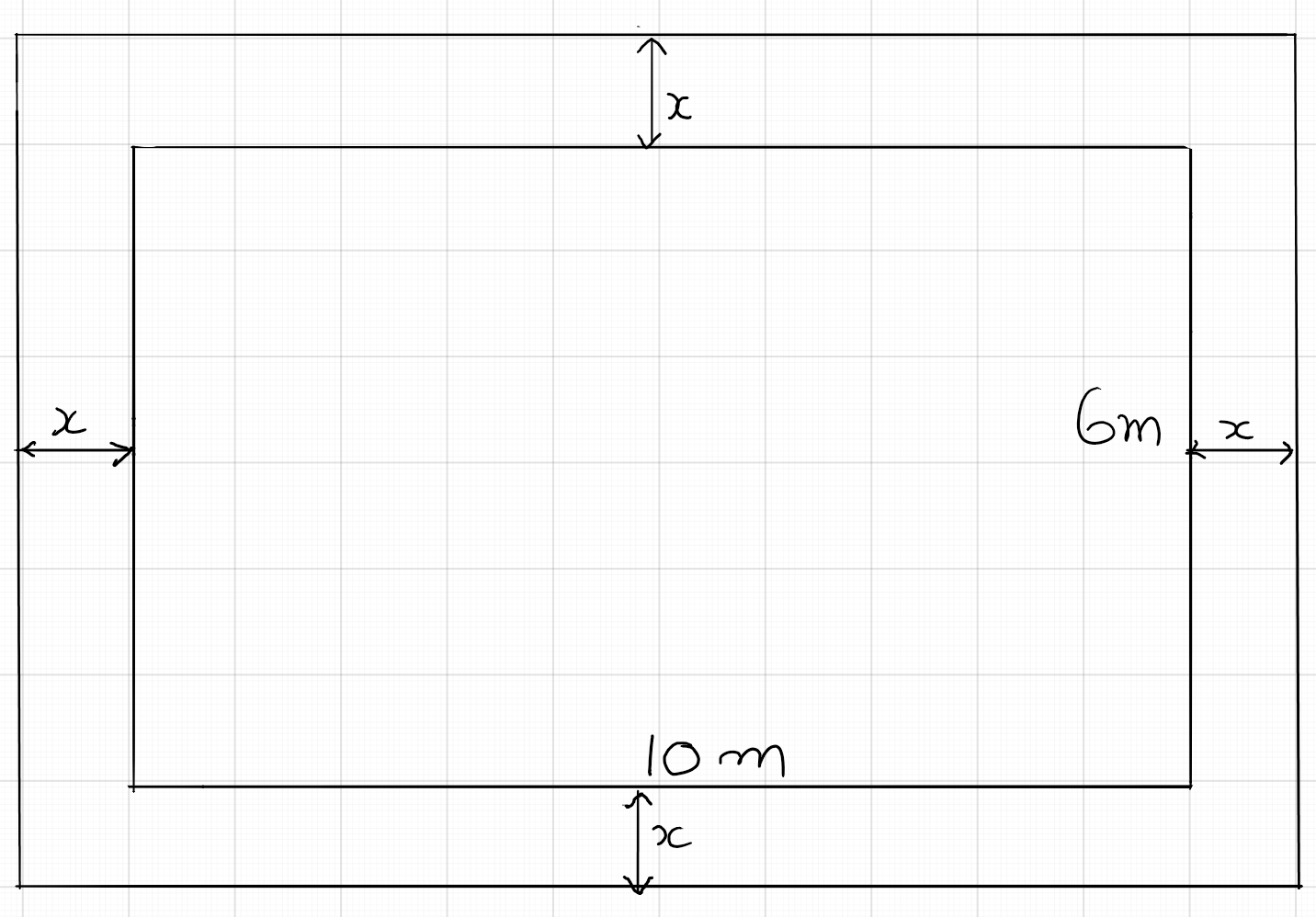
A swimming pool 6 m wide and 10 m long is surrounded by a walkway of uniform width. The area of the walkway is equal to the area of the pool. Find the width of the walkway.

Solution:

This problem is best understood by drawing a diagram to represent the swimming pool and the walkway. The diagram is shown at the bottom.
Let the width of the walk way be $x$ m. The area of the swimming pool is $6 x 10 = 60 m^2$/ Area of the outer rectangle that includes the pool and the walkway is double this area, as the area of the walkway is given to be equal to the area of the pool. The length and width of the outer rectangle are $6 + 2x$ and $10 + 2x$ respectively. Setting up the equation and solving: \begin{eqnarray} (6 + 2x)(10 + 2x) &=& 120\\ 60 + 12x + 20x + 4x^2 &=& 120\\ 4x^2 + 32x + 60 - 120 &=& 0\\ 4x^2 + 32x - 60 &=& 0\\ x^2 + 8x - 15 &=& 0\\ x &=& \frac{-8 \pm \sqrt{8^2 - 4(1)(-15)}}{2}\\ &=& \frac{-8 \pm \sqrt{64 + 60}}{2}\\ &=& \frac{-8 \pm \sqrt{124}}{2}\\ &=& \frac{-8 \pm 2\sqrt{31}}{2}\\ &=& -4 \pm \sqrt{31}\\ \end{eqnarray} As $-4 -\sqrt{31}$ gives a negative value which is not possible, the width of the walkway is $-4 + \sqrt{31}$ m.

Working alone, Anand takes two more hours to clean the house than Anita does. If they work together, Anand and Anita can clean the house in 2 hours and 24 minutes. How long does Anand take to clean the house if he is working alone

Solution:

Let $x$ be the number of hours Anand takes to clean the house alone. then in one hour, he would clean $\frac{1}{x}$ of the house.
Given that Anand takes two more hours to clean the house than Anita. So, Anita takes $x - 2$ hours to clean the house alone. So,in one hour, Anita would clean $\frac{1}{x-2}$ of the house.
Both of them together would clean $\frac{1}{x} + \frac{1}{x-2}$ of the house in one hour.
Given that together, they clean the house in 2 hours and 24 minutes, i.e., $2\frac{24}{60} = 2\frac{2}{5} = \frac{12}{5}$ hours. So, in one hour, they clean $\frac{5}{12}$ of the house.
This means that $$\frac{1}{x} + \frac{1}{x-2} = \frac{5}{12}$$. Multiplying each term on both sides by the LCM $12x(x-2)$ and solving for $x$: \begin{eqnarray} 12(x-2) + 12x &=& 5x(x-2)\\ 12x - 24 + 12x &=& 5x^2 - 10x\\ 5x^2 - 34x + 24 &=& 0\\ x &=& \frac{34 \pm \sqrt{34^2 - 4(5)(24)}}{10}\\ &=& \frac{34 \pm \sqrt{676}}{10}\\ &=& \frac{34 \pm 26}{10}\\ x &=& \frac{34 + 26}{10} \implies x = 6\\ x &=& \frac{34 - 26}{10} \implies x = 0.8\\ \end{eqnarray} If $x = 0.8$, $x-2 = -1.2$, which is negative. So, the correct answer is $x = 6$. That is, Anand takes 6 hours to clean the house alone.

The numerator of a fraction is 1 less than its denominator. when both numerator and denominator are increased by 2, the fraction is increased by $\frac{1}{12}$. Find the original fraction.

Solution:

Let the denominator of the original fraction by $x$. Then, its numerator is $x-1$, thus the original fraction is $\frac{x-1}{x}$. When both numerator and the denominator are increased by 2,the fraction becomes $\frac{x-1+2}{x+2} = \frac{x+1}{x+2}$. Given that, $$ \frac{x+1}{x+2} = \frac{x-1}{x} + \frac{1}{12}$$. Multiplying each term on both sides by the LCM $12x(x+2)$ and solving for $x$, we get: \begin{eqnarray} \frac{x+1}{x+2} &=& \frac{x-1}{x} + \frac{1}{12}\\ 12x(x+1) &=& 12(x+2)(x-1)+x(x+2)\\ 12x^2+12x &=& 12x^2+12x-24+x^2+2x\\ x^2+2x-24 &=& 0\\(x+6)(x-4) &=& 0\\ x+6 &=& 0\implies x=-6\\x-4 &=& 0 \implies x=4\\ \end{eqnarray} Discarding the negative value, we get $x=4$. So, the original fraction is $\frac{3}{4}$. We can verify that $\frac{3}{4}+ \frac{1}{12} = \frac{5}{6}$, which can be obtained by increasing both numerator and denominator by 2.

Each side of a square is 4 metres. When each side is increased by $x$m, the area of the square is doubled. Find the value of $x$.

Solution:

Each side of the square is 4m. So, are area is 16sq.m. If each side of the square is increased by $x$m, the length of each side becomes $x+4$m. So, the new area is $(x+4)^2$. This area is given to be twice the area of the original square. Setting up the equation and solving, we get: \begin{eqnarray} (x+4)^2 &=& 32\\ x+4 &=& \pm \sqrt{32}\\ &=& 4\sqrt{2}\\ x &=& -4\pm4\sqrt{2}\\ x &=& -4+4\sqrt{2} \implies x \approx 1.64\\ x &=& -4-4\sqrt{2} \implies x \approx -9.64\\ \end{eqnarray} Discarding the negative value, we have the value of $x = 1.64$m