Mathematics at Aksharam
Want to share an opinion?—drop a mail
Dr. Lalitha Subramanian, About the Author
A linear equation in two variables is typically of the form $ax + by + c = 0$, where $a$ and $b$ are not both zero. Solution for such an equation is a pair of values, $ x = p, y = q$. Depending on the value of $x$ we put in, we get a corresponding value of $y$. In this sense, this equation has infinite pairs of solutions. These pairs of values correspond to the coordinates $(x,y)$ of infinite number of points on the line which is called the graph of the line. So, we can say that there is a one-to-one correspondence between the points on the line that is the graph of the equation and the pair of solutions of the equation. That is, any pair of solution to the equation corresponds to a point on the line, and the coordinates of any point on the line corresponds to a pair of solution to the equation.
Check if the following points lie on the line whose equation is $2x - 3y + 1 = 0$: $(a) (1, 4); \quad (b) (3, 2); \quad (c) (1, 1); \quad (d) (2, -1)$
Solution:
First let us rewrite the given equation as $2x - 3y = - 1$.
$(a)$ Substituting $x = 1$ and $y = 4$ in the equation gives $2(1) - 3(4) = 2 - 12 = - 10 \neq -1$. So, this point does not lie on
the line represented by the given equation.
$(b)$ Substituting the values of the coordinates on the given equation gives
$2(3) - 3(2) = 6 - 6 = 0 \neq -1$. So, this point does not lie on the line of the given equation.
$(c)$ Substituting the
coordinates on the given equation gives $2(1) - 3(1) = 2 - 3 = - 1 = -1$ So, this point lies on the given line.
$(d)$ Substituting
the coordinates on the given equation gives $2(2) - 3(-1) = 4 + 1 = 7 \neq - 1$. So, this point does not lie on the given line.
Consider two such equations, taken together. If a pair of solutions $(x,y)$ satisfy both equations, the point represented by the coordinates $(x,y)$ lies on the graphs of both lines defined by these equations. Thus, the solution set of a pair of linear equations in two variables represent the coordinates of the point of intersection of the graphs of the two equations.
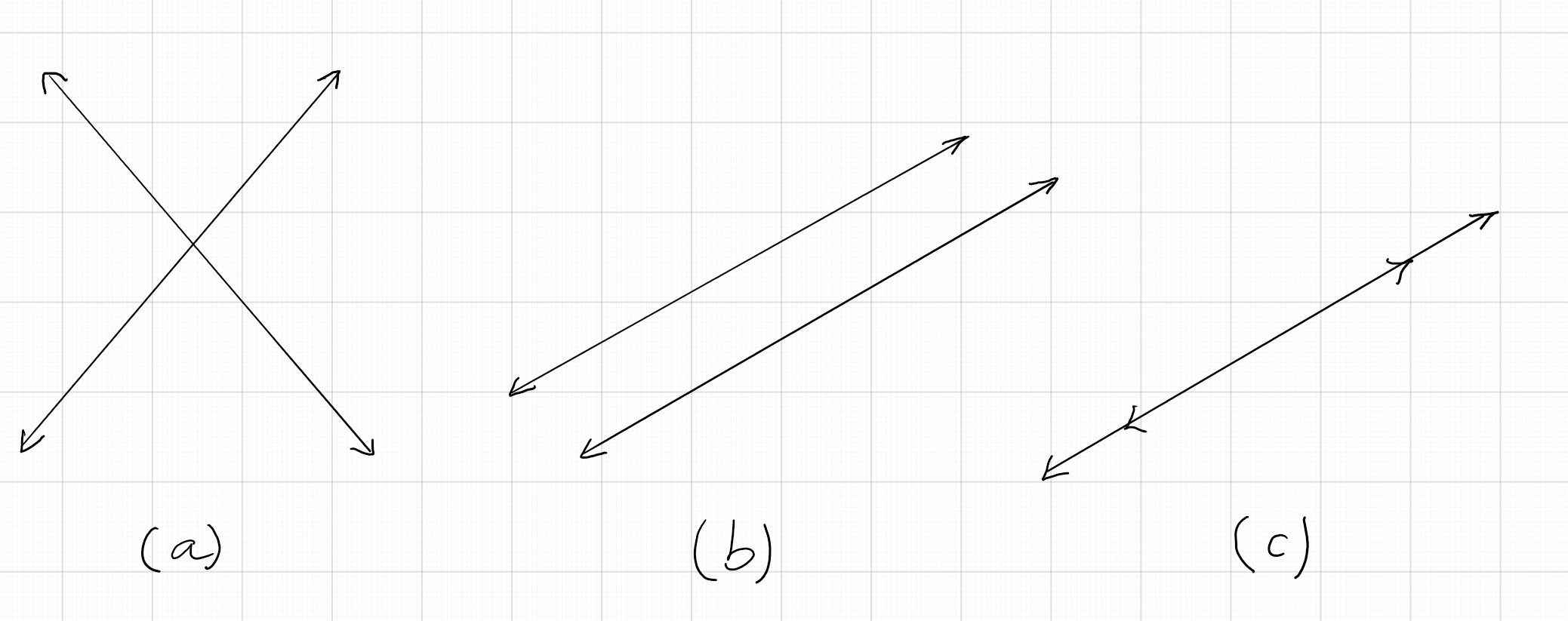
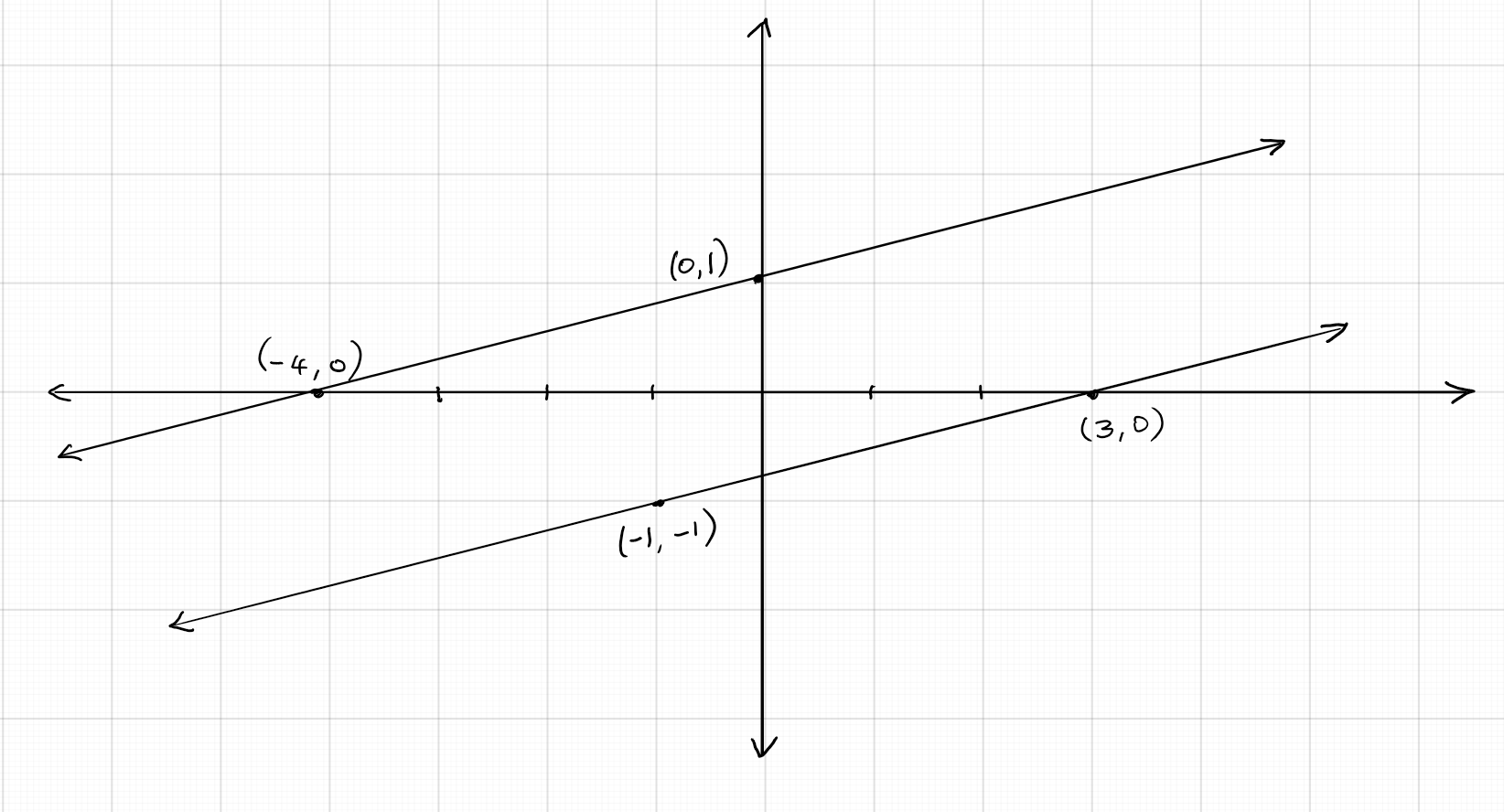
Given two lines in a plane, (a) the two lines may intersect, (b) They may be parallel, or (c) they may coincide as one line.
(a) If the two lines intersect,
they do so at exactly one point, and the coordinates of this point is the pair of solutions to the pair of given linear equations. Thus, the pair of equations
have a unique pair of solutions. These types of pairs of equations are called consistent pair of equations.
(b) If the two lines are parallel,
they do not intersect at all. So, the pair of liner equations yield no solution. Such types are called inconsistent pair of equations.
(c) If the two lines coincide, all the points on the line are solutions to both equations.
So, the pair have infinitely many pairs of solutions. Such pairs of equations are called dependent pair of equations. The graphs below show the three types of pairs of lines:
Consider a pair of linear equations $a_{1}x + b_{1}y + c_{1} = 0$ and $a_{2}x + b_{2}y + c_{2} = 0$. The ratios of the corresponding coefficients are
$\frac{a_{1}}{a_{2}}$. $\frac{b_{1}}{b){2}}$, and $\frac{c_{1}}{c_{2}}$.
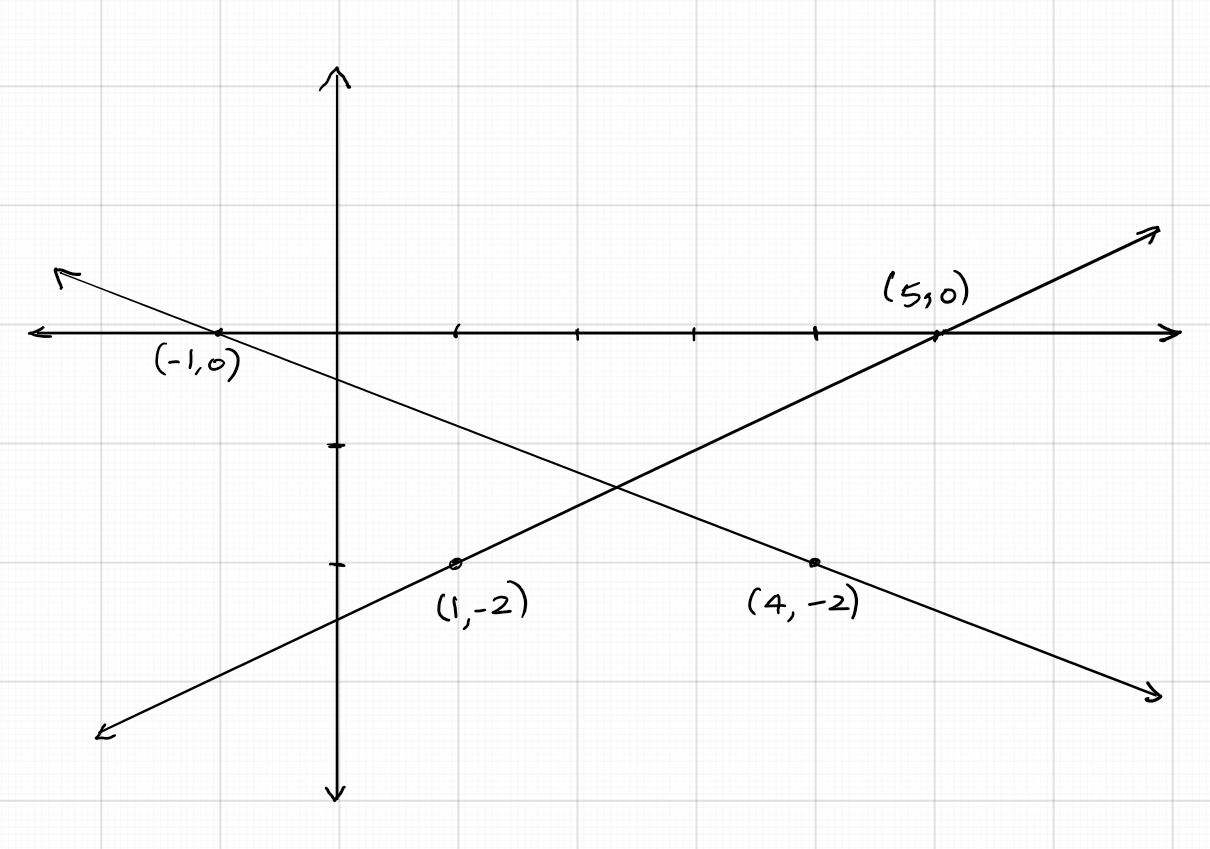
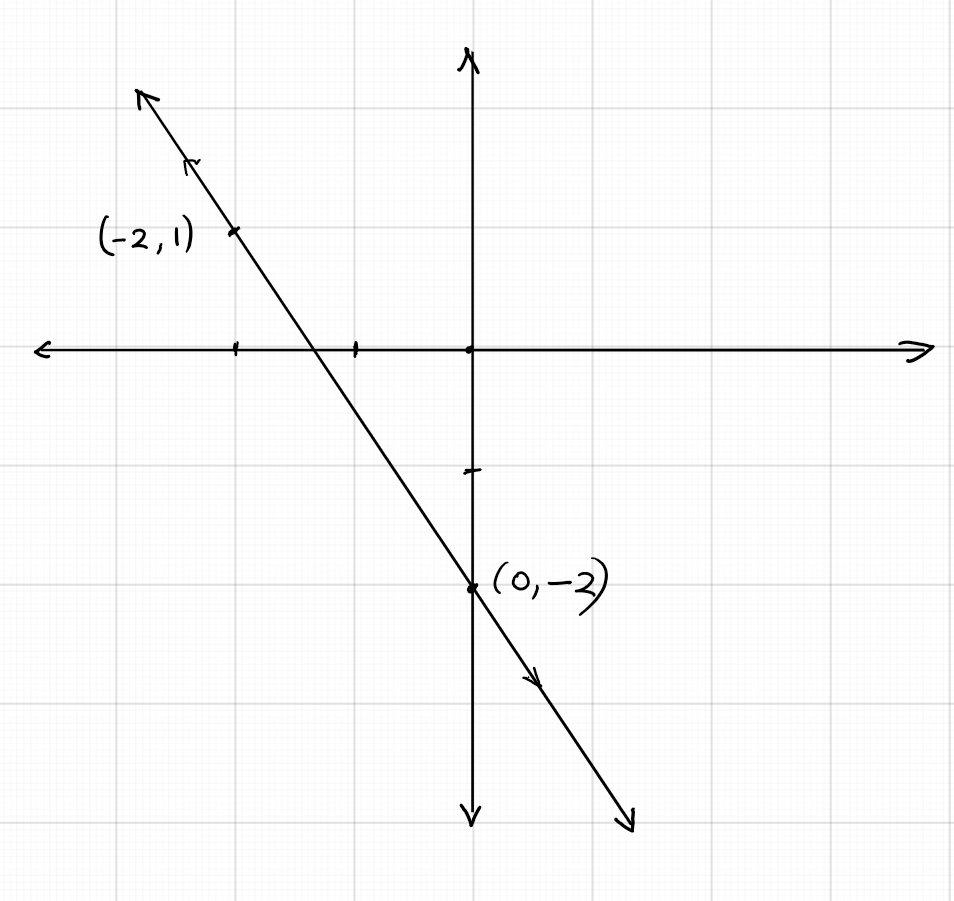
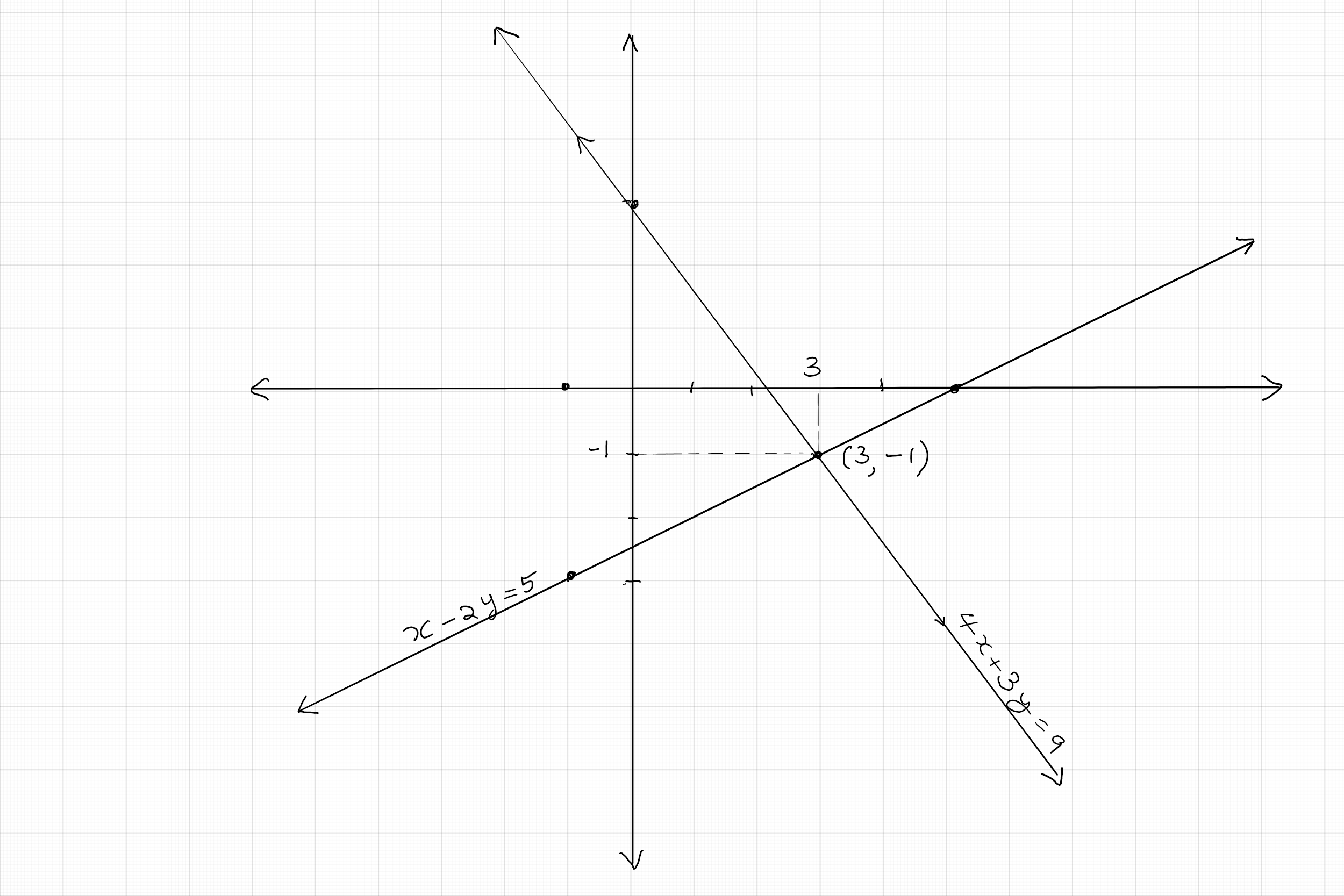
Determine whether each of the following pairs of equations are consistent, inconsistent, or dependent by graphing
the equations:
$(a) x- 3y = 6; 2x + y = 4; \quad (b) x + 2y = 8; 2x + 4y = 10; \quad (c) 2x - 3y = 9; 4x - 6y = 18.$
Solution:
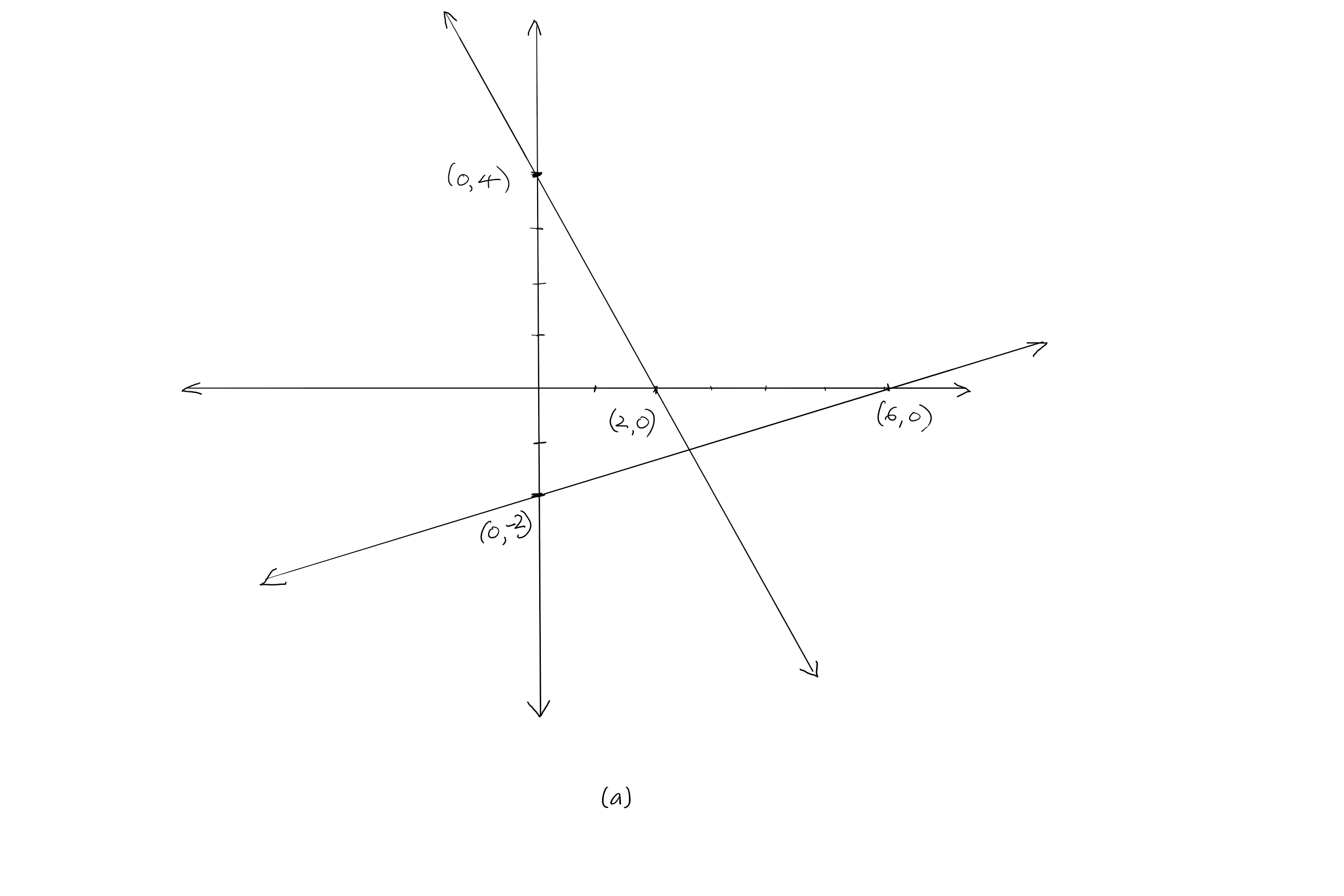
$(a)$ Find two points on the graph of the first equation: $(0, -2), (6,0)$.Two points on the graph of the second
equation: $(0,4), (2, 0)$. The graph shows that the two lines intersect at a point; So, this pair of equations is consistent.
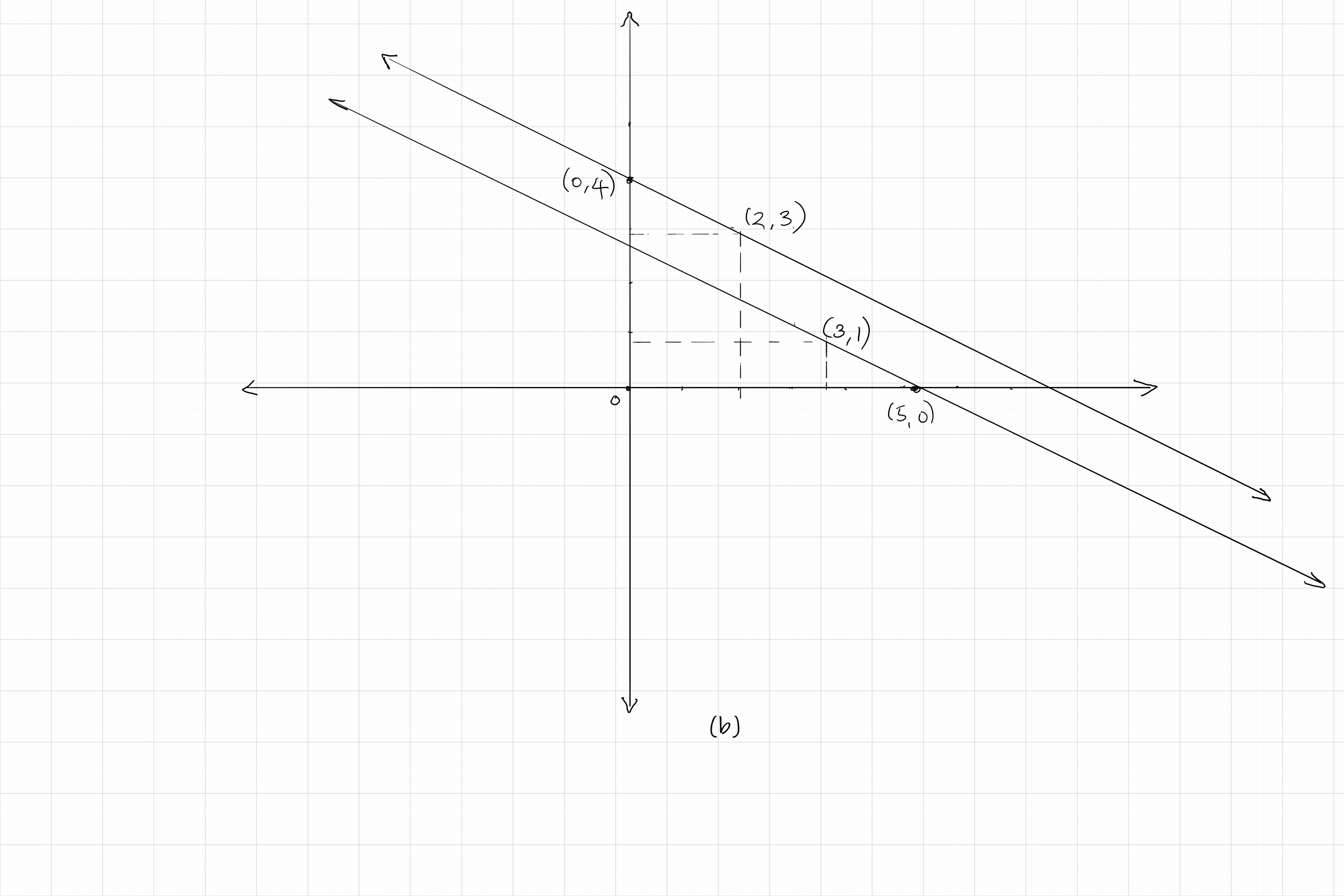
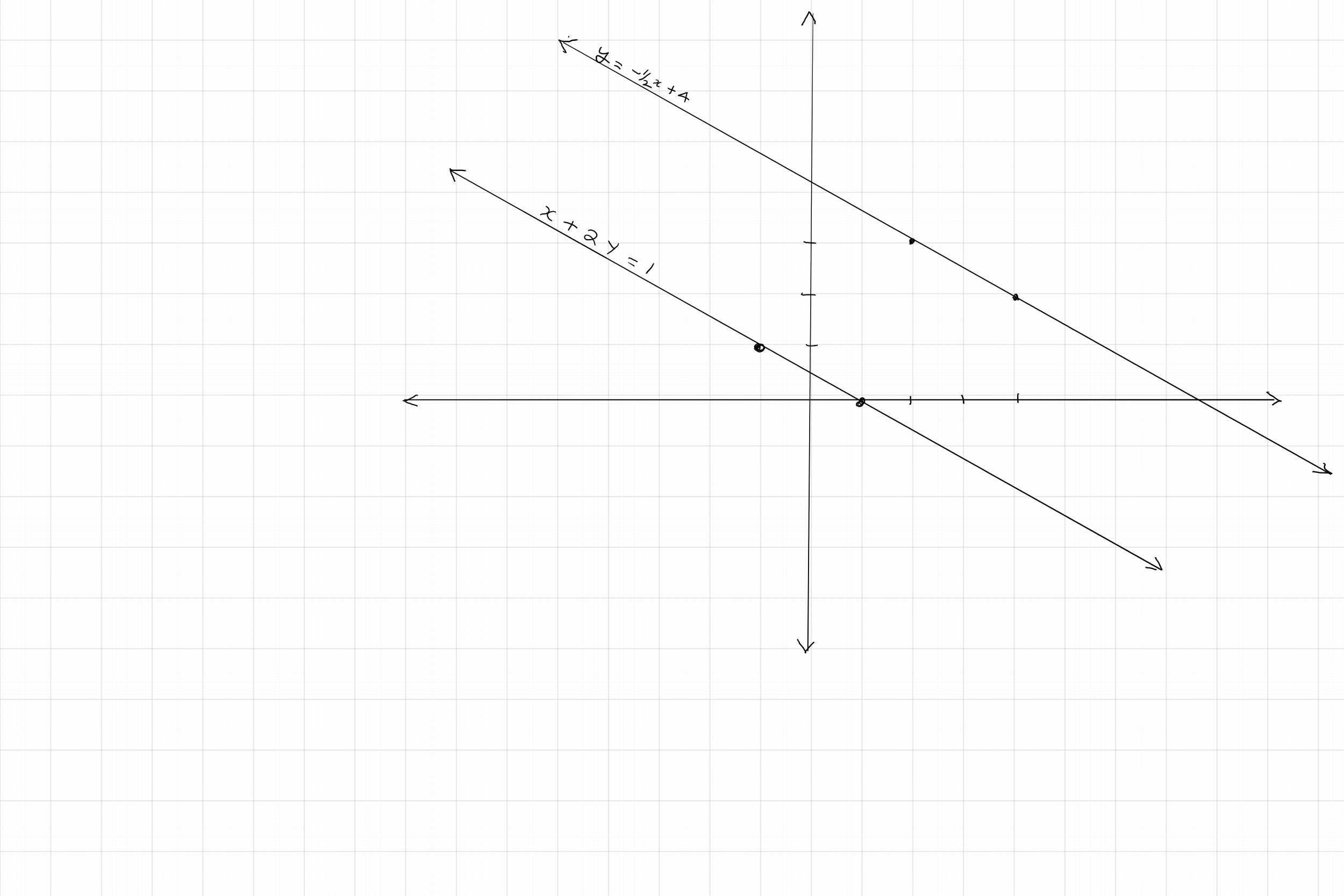
$(b)$ Two points on the graph of the first equation: $(0, 4), (2, 3)$ and two points on the graph of the second equation: $(5, 0), (3, 1)$.
The graph below shows that the two lines are parallel. So, this pair of equations is inconsistent.
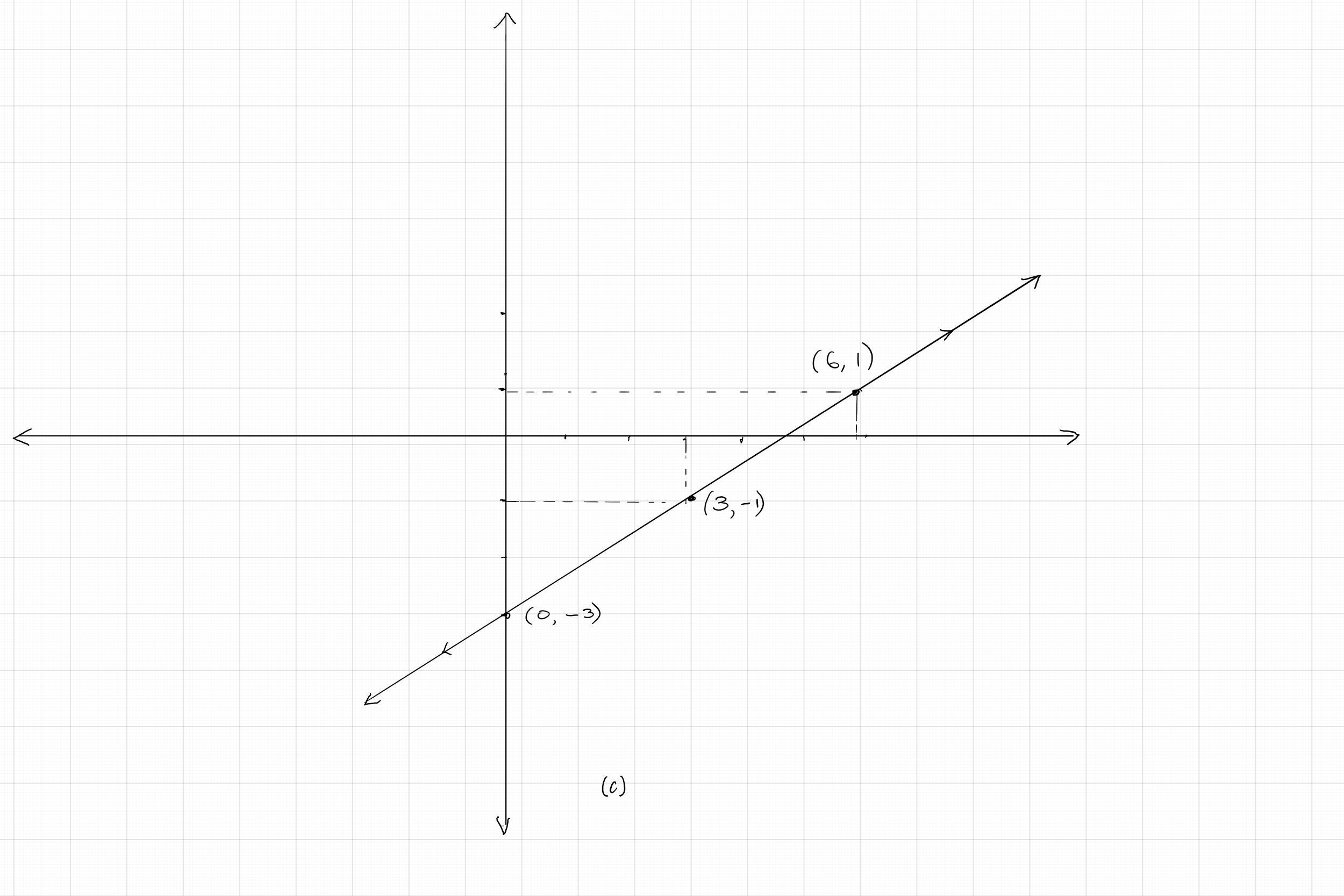
$(c)$ Two points on the graph of the first equation: $(0, -3), (3, - 1)$; Two points on the graph of the second equation: $(6, 1), (0, - 3)$. The graph below shows that the
two lines coincide. So, this pair equations is dependent.
Determine algebraically whether each of the following pairs of equation are consistent, inconsistent, and dependent: $(a) x - y = 4; 2x - 2y = 4; \quad (b) 3x + y = 7; x+ 3y = 9; \quad (c) 4x + 2y = 6; 2x + y = 3.$
Solution:
$(a)$ Comparing the ratios of coefficients of $x$ and $y$, we have $\frac{1}{2} = \frac{-1}{-2}$.
But we note that the ratio of the constant terms $\frac{4}{4} \neq \frac{1}{2}$. So, this pair of equations is
inconsistent and has no solution. The graph of this pair represent parallel lines; $(b)$ Comparing the ratios of the
coefficients of $x$ and $y$, we have $\frac{3}{1} \neq \frac{1}{3}$. So, this pair of equations is consistent and has a
unique solution. The graph of this pair represent intersecting lines;
$(c)$ Comparing the ratios of the coefficients
of $x$ and $y$, we have $\frac{4}{2} = \frac{2}{1}$. We note that the ratio of the constant term $\frac{6}{3} = \frac{2}{1}$.
This means all the ratios of corresponding terms are equal. So, this pair of equations is dependent and has infinitely
many solutions. The graph of this pair represent two coinciding lines.
The above discussions and examples lead to a good method of solving a pair of linear equations in two variables using graphs.
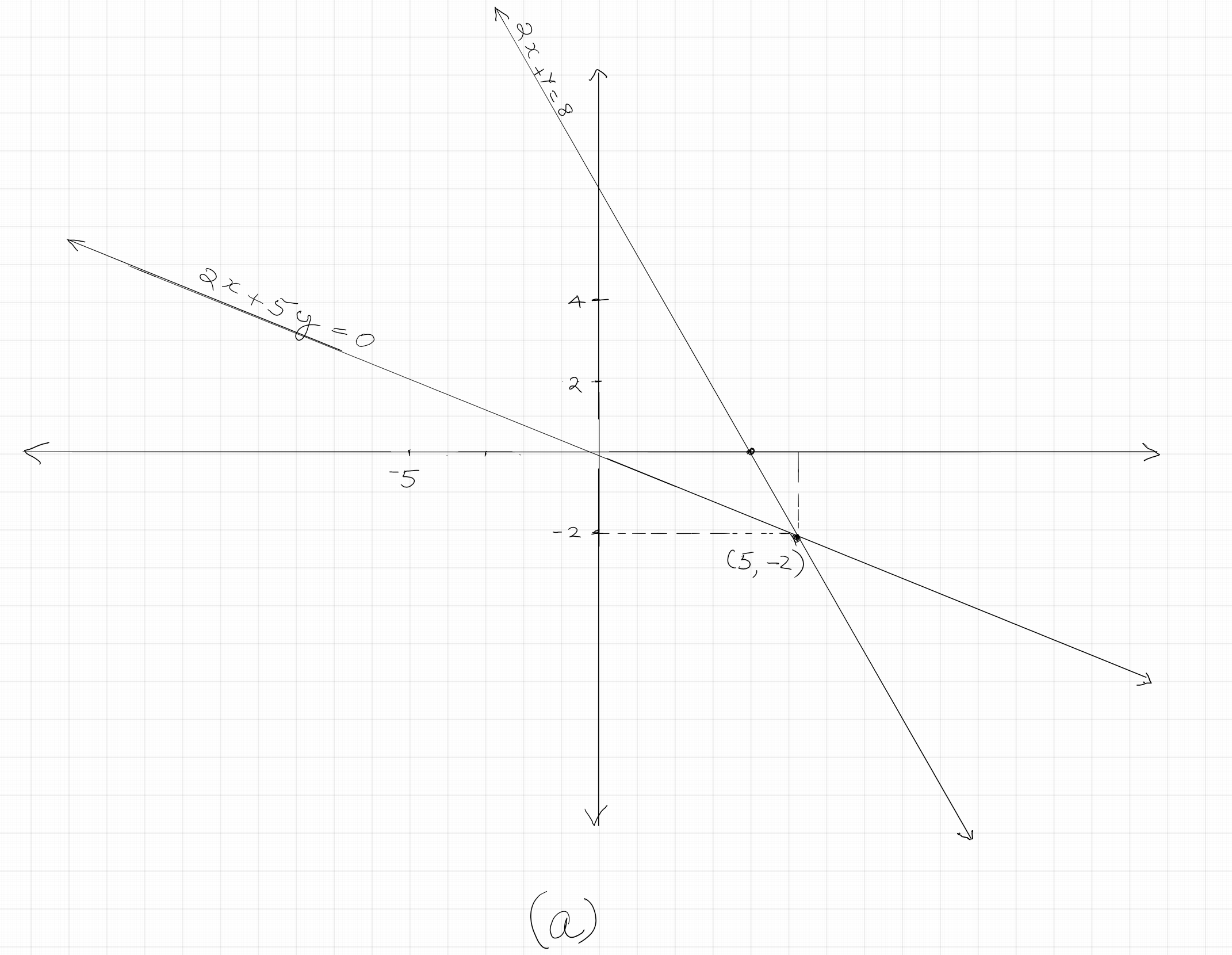
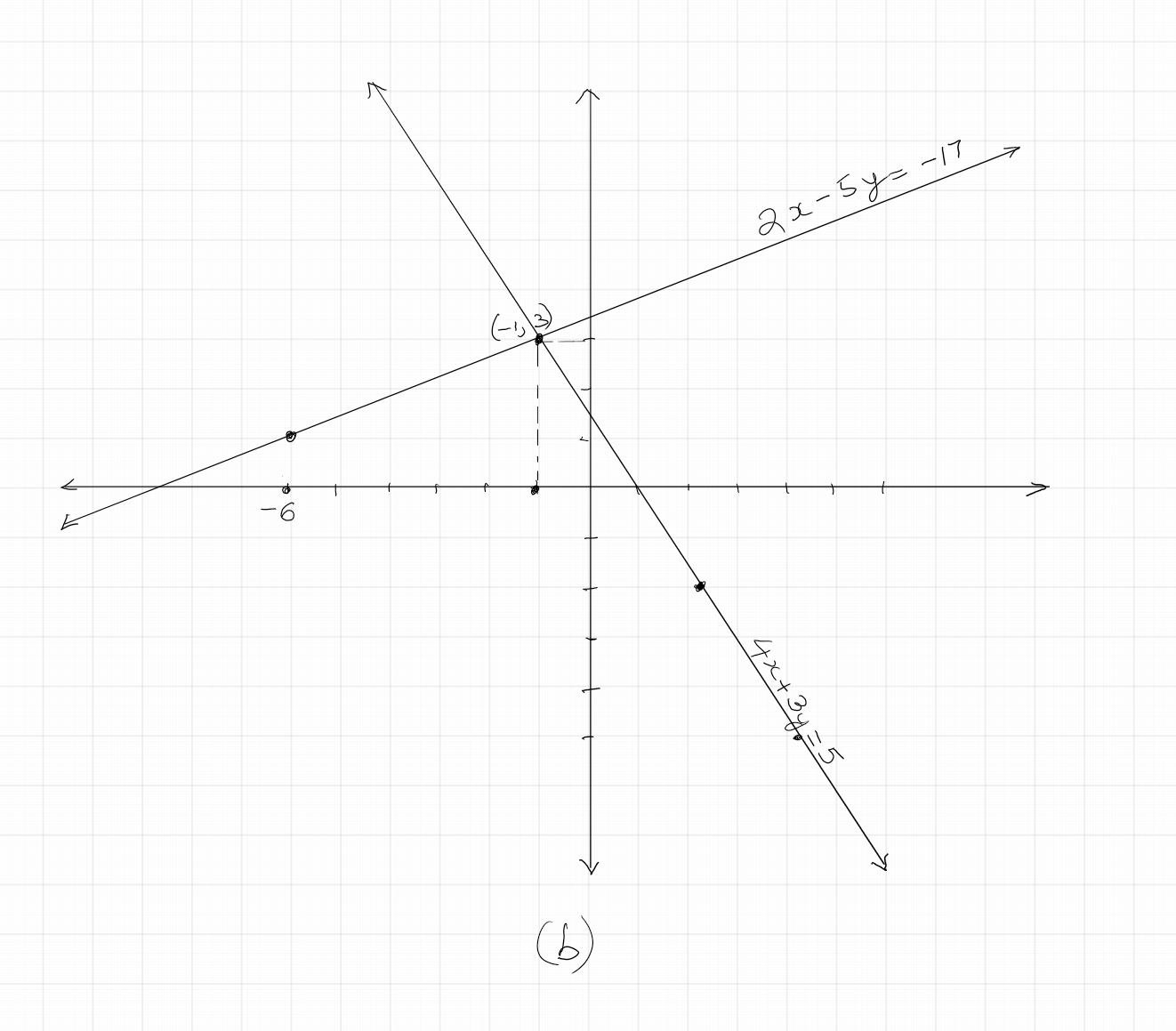
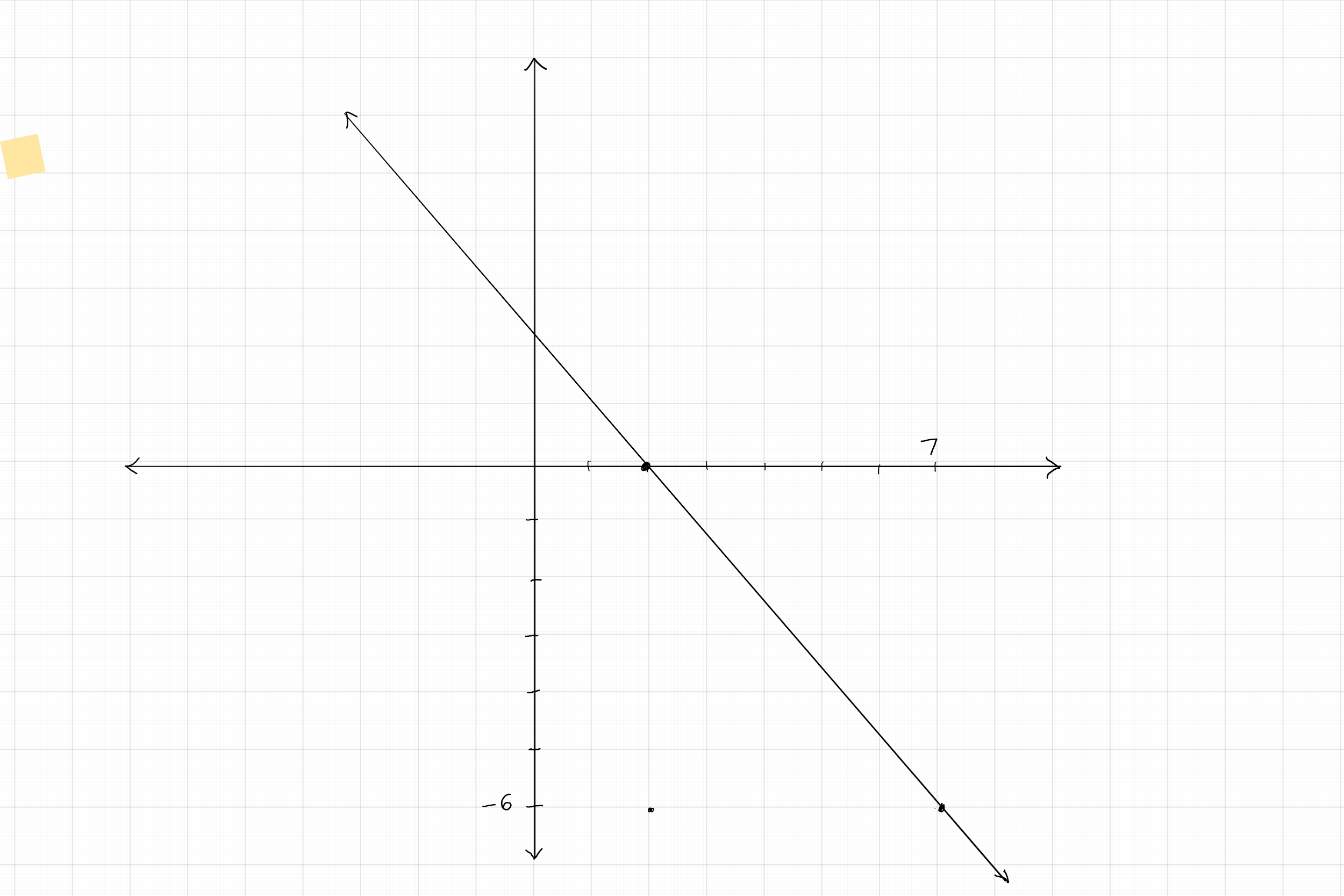
Solve each of the following pairs of linear equations by graphing: $(a) 2x+ 5y = 0; 2x + y = 8; \quad (b) 4x + 3y = 5; 2x - 5y = -17$
Solution:
$(a)$ The graph below shows the two lines corresponding to these equations intersecting at the point $(5, - 2)$. So, the solution set is $\{x = 5, y - - 2\}$.
$(b)$ The graph below shows the point of intersection of the two lines corresponding these two equations to be $(-1, 3)$. So, the solution set is $\{x = - 1, y = 3\}$.
$(c)$ The graph below shows the point of intersection of the lines to be $\left(4, -\frac{1}{2}\right)$. So, the solution set is $\{x = 4. y = -\frac{1}{2}\}$.
If the graphs of the lines corresponding to the two given equations are parallel, then we conclude the system has no solution, and call it as inconsistent system. If the graphs coincide into the same line, then we conclude that the system has infinitely many solutions, and call it dependent system.
Consistent.
Dependent.
Inconsistent.
Inconsistent.
Consistent.
Dependent.
Solution of the system is $(3, -1)$
The system is inconsistent. No solution.
The system is dependent system, with infinitely many solutions.
We can solve a system of two linear equations in two variable in any one of the following methods:
Substitution method is most convenient when the coefficient of one of the variables in any one equation is unity. The examples below illustrate this method.
Solve each of the following pair of equations using the method of substitution: $(a) x + 2y = 8; 2x - 3y = 23; \quad (b) x - 3y = 6; 2x + y = 5.$
Solution:
$(a)$ The coefficient of $x$ in the first equation is unity. First, let us rewrite this equation and express $x$ in terms of $y$: $x = -2y + 8$. Now we shall
substitute this for $x$ in the second equation, and solve for $y$ first, and then solve for $x$: \begin{eqnarray} 2(-2y + 8) - 3y &=& 23\\
-4y + 16 - 3y &=& 23\\ - 7y + 16 &=& 23\\ -7y &=& 7\\ y &=& - 1\\ x &=& -2(-1) + 8\\ &=& 10\\ \end{eqnarray}
$(b)$ In this problem, coefficient of $x$ in the first equation as well as the coefficient of $y$ in the second equation is unity.
Hence, we can choose either of these equations for substitution. Let us take the second equation and express $y$ in terms of $x$: $y = - 2x + 5$.
Now, we shall substitute the expression of $y$ in the first equation, and solve for $y$, and then solve for $x$. \begin{eqnarray} x - 3(-2x+ 5) &=& 6\\ x + 6x - 15 &=& 6\\
7x - 15 &=& 6\\ 7x &=& 21\\ x &=& 3\\ y &=& -2(3) + 5\\ &=& - 1\\ \end{eqnarray}
Elimination method is perhaps most frequently used due to its ease of process. In this method, we eliminate one of the variables from the pair, by making their coefficients equal and opposite, and then adding the equations. Once we solve for the remaining variable, we substitute that value in any one of the original equations to get the solution for the other variable. Examples shown below illustrate this process.
Solve each of the following pair of equations by elimination: $(a) 3x - 5y = 4; 9x - 2y = 7; \quad (b) x - 3y = 7; 3x - 3y = 15.$
Solution:
$(a)$ Observe the coefficients of the variables in each equation. As the coefficient of $x$ in the first equation can be made to be
equal and opposite to the coefficient of $x$ in the second equation by multiplying the first equation by $-3$, we shall decide to eliminate $x$:
\begin{eqnarray} 9x - 2y &=& 7 \\ -9x + 15y &=& -12 \\ 13x &=& - 5\\ x &=& -\frac{5}{13}\\ 9x - 2\left(-\frac{5}{13}\right) &=& 7 \\
9x &=& \frac{81}{13}\\ 9x + \frac{10}{13} &=& 7 \\ 9x &=& 7 - \frac{10}{13}\\ 9x &=& \frac{81}{13}\\
x &=& \frac{81}{9 \times 13}\\ x &=& \frac{9}{13}\\ \end{eqnarray}
$(b)$ In this pair, the variable $y$ has the same coefficients on both equations. We can multiply one of the equations by $-1$ to make them opposite
sign, and then add the two equations to cancel the $y$ terms so that we can solve for $x$. Then, we can substitute the value of $x$ in one of the pairs to
obtain the value of $y$: \begin{eqnarray} x - 3y &=& 7\\ - 3x + 3y &=& -15\\ -2x &=& -8\\ x &=& 4 - 3y &=& 7\\
-3y &=& 3\\ y &=& -1\\ \end{eqnarray}
Using the elimination method on a pair of general linear equations in two variables $a_{1}x + b_{1}y + c_{1} = 0$
and $a_{2}x + b_{2}y + c_{2} = 0$, we get the values of the variables in terms of the unknown constants as
$x = \frac{b_{1}c_{2} - b_{2}c_{1}}{a_{1}b_{2} - a_{2}b_{1}}$ and
$y = \frac{c_{1}a_{2} - c_{2}a_{1}}{a_{1}b_{2} - a_{2}b_{1}}$. Here, if the denominator $a_{1}b_{2} - a_{2}b_{1} = 0$,
this would mean that $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}$, two cases arise:
if $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$, then the system has infinitely many solutions,
as we have already seen that this pair would result in graph of lines that coincide into one another.
If $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}$, then the system has no solution as they
graph as two parallel lines.
If $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$, then the system has a unique solution.
We can simplify the solutions as: $$ \frac{x}{b_{1}c_{2} - b_{2}c_{1}} = \frac{y}{c_{1}a_{2} - c_{2}a_{1}}
= \frac{1}{a_{1}b_{2} - a_{2}b_{1}}$$.
This expression can be easily remembered by making the following diagram that shows cross multiplication
of the unknown constants appropriately. Due to the ease of this diagram, this method is sometimes called
cross multiplication method
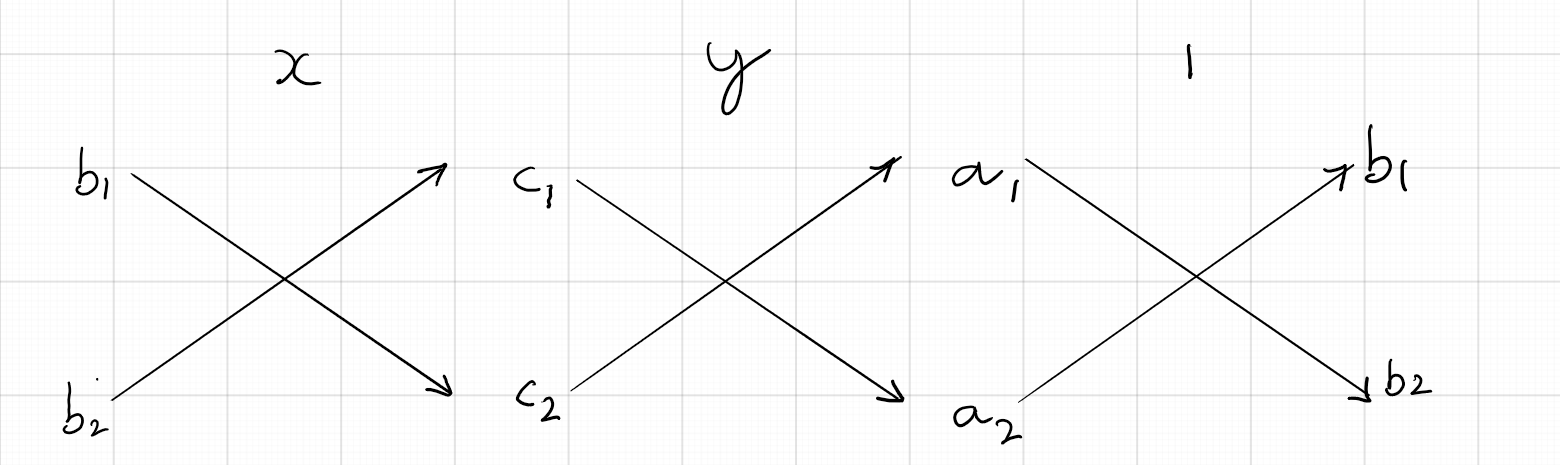
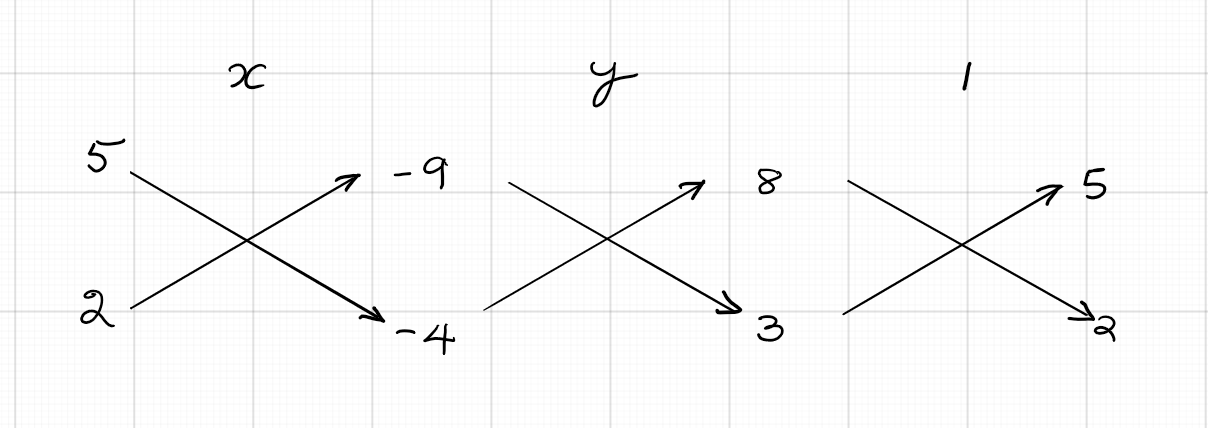
Solve using cross multiplication method: $8x + 5y = 9; 3x + 2y = 4$
Solution:
First we shall rewrite these equations in standard form: $8x + 5y - 9 = 0; 3x + 2y - 4 = 0$. From the diagram below, we have $\frac{x}{-20 + 18} = \frac{y}{-27 + 32} = \frac{1}{16 - 15}$. On simplifying, we get $\frac{x}{-2} = \frac{y}{5} = \frac{1}{1}$. So, solution set is $x = - 2; y = 5$
The example below illustrate a method to find unknown constant, under given condition:
For which value of $a$ and $b$ will the following pair of equations have in infinitely many solutions: $2x + 3y = 7; (a - b)x + (a + b)y = 3a + b - 2$
Solution:
A pair of equations will have infinite number of solutions if and only if the equations are equivalent. That is the ratio of the corresponding coefficients are equal. So, we have $$\frac{2}{(a-b)} = \frac{3}{(a+b)} = \frac{7}{3a+b-2}$$. Setting the first two ratios equal, we have: \begin{eqnarray} \frac{2}{(a-b)} &=& \frac{3}{(a+b)}\\ 2(a+b) &=& 3(a-b)\\ 2a + 2b &=& 3a - 3b\\ a - 5b &=& 0\\ \end{eqnarray} Let us call this equation $(1)$. To get the second equation, we set the first and the third ratios equal: \begin{eqnarray}\frac{2}{(a - b)} &=& \frac{7}{(3a + b - 2)}\\ 7(a - b) &=& 2(3a = b - 2)\\ 7a - 7b &=& 6a - 5b &=& 6a + 2b - 4\\ a - 9b &=& - 4\\ \end{eqnarray} Let us call this equation $(2)$. Now, solving equations $(1)$ and $(2)$ by elimination, we have: \begin{eqnarray} a - 5b &=& 0\\-a + 9b &=& 4\\ 4b &=& 4\\ b &=& 1\\ a - 5(1) &=& 0\\ a - 5 &=& 0\\ a &=& 5\\ \end{eqnarray} So, the given pair of equations will have infinitely many solutions for $a = 5$ and $b= 1$
Some pair of equations in two variables can be solved by reducing them into the standard form by suitable substitutions. This will enable us to solve for the required variables more conveniently. The examples below illustrate this:
Solve using suitable method: $(a) \frac{6}{u} + \frac{3}{v} = 2; \frac{2}{u} - \frac{9}{v} = 4; \quad (b) \frac{5}{x - 1} + \frac{1}{y - 2} = 2; \frac{6}{x - 1} - \frac{3}{y - 2} = 1$
Solution:
$(a)$ Substituting $\frac{1}{u} = x$ and $\frac{1}{v} = y$, we can rewrite the equations as $6x + 3y = 2$ and $2x - 9y = 4$. Multiplying
the first equation by$3$ and adding to the second equation eliminates $y$ so that we can solve for $x$. Then, substituting the value of $x$ in one of the above
equations would produce the value of $y$: \begin{eqnarray} 2x - 9y &=& 4\\ 18x + 9y &=& 6\\ 20x &=& 10\\ x &=& \frac{1}{2}\\ 2\left(\frac{1}{2}\right) - 9y &=& 4\\
1 - 9y &=& 4\\ - 9y &=& 3\\ y &=& -\frac{1}{3}\\ \end{eqnarray}
Now we have $x = \frac{1}{u} = \frac{1}{2} \implies u = 2$. Also,
$y = \frac{1}{v} = - \frac{1}{3} \implies v = - 3$.
$(b)$ For this problem, let us substutitue $a = \frac{1}{x - 1}$ and $b = \frac{1}{y - 2}$.
Then, we can rewrite the equations as $5a + b = 2$ and $6a - 3b = 1$. Multiplying the first equation by $3$ and adding eliminates $b$ so that solution for $a$ is
obtained. Then, by substituting this value in one of the above equations would give the value of $b$: \begin{eqnarray} 6a - 3b &=& 1\\ 15a + 3b &=& 6\\
21a &=& 7\\ a &=& \frac{1}{3}\\ 6\left(\frac{1}{3}\right) - 3b &=& 1\\ 2 - 3b &=& 1\\ -3b &=& -1\\ b &=& \frac{1}{3}\\ \end{eqnarray}
Sustituting the values of $a$ and $b$ in our original assumptions gives the solution set for this problem: \begin{eqnarray} a &=& \frac{1}{3}\\ \frac{1}{x - 1} &=&
\frac{1}{3}\\ x - 1 &=& 3\\ x &=& 4\\ \end{eqnarray}
\begin{eqnarray} b &=& \frac{1}{3}\\ \frac{1}{y - 2} &=& \frac{1}{3}\\ y - 2 &=& 3\\
y &=& 5\\ \end{eqnarray}
For problems # 1 - 5, identify each pair of equations as consistent,inconsistent, or dependent. If the pair is consistent, determine the solution set using substitution method:
Consistent; $x = 3, y = -1$.
Inconsistent. No solutions as the lines are parallel.
Consistent; $x = 3, y = - 5$
Dependent system; infinite number of solutions.
Consistent; $x = - 4, y = - 2$
Unique solution: $x = - 3; y = 5$.
Infinte number of solutions.
Unique solution; $x = 4, y = -\frac{1}{2}$
No solution.
Unique solution: $x = 2, y = - 1$.
For problems #11 - 15, solve each pair of linear equations by cross multiplication method.
$x = 3, y = 1$
Infinite number of solutions.
$x = - 1, y = 3$
$x = 2; y = 1$
$x = 4; y = 3$.
For problems #15 - 18. reduce each sysem to linear equations in two variables and hence solve the system.
$u = - 2; v = 3$
$ u = \frac{1}{2}; v = 2$
$u = \frac{2}{3}; v = - 1$
Problem solving typically involves solving a real life situation using a mathematic model. Following steps help us make the process easier:
The examples below illustrate the process. We use two variables in these problems and form two linear equations based on the given information. Then, solve the problem.
Preet scored 50 marks in a test, getting 3 marks for each right answer and losing 1 mark for every wrong answer. He would have scored 60 marks is 4 marks were awarded to each right answer and $-2$ marks were given for each wrong answer. How many questions were there in the test?
Solution:
Let the number of answers Preet got right be $x$ and the number of answers he got wrong be $y$. Then, according to the given information, we have two
linear equations $3x - y = 50$ and $4x - 2y = 60$. We can eliminate $y$ by multiplying the first equation by $(-2)$ and adding to the second equation:
\begin{eqnarray} - 6x + 2y &=& - 100\\ 4x - 2y &=& 60\\ - 2x &=& - 40\\ x &=& 20\\ 3(20) - y &=& 50\\ -y &=& - 10\\ y &=& 10\\ \end{eqnarray}
Answer: Preet got 20 anwers right and 10 answers wrong. So, total number of questions in the test was 30.
The perimeter of a rectangle is 36 metres and the length is 2 metres more than three times its width. Find the dmensions of the rectangle.
Solution:
Let the length and width of the rectangle be $l$ and $w$ respectively. Then, according to the given information, we have first equation $2(l + w) = 36$. Dividing
the equation by $2$, we have $l + w= 18$. The second equation is obtained by translating the second information into mathematical sentence: $ l = 3w + 2$. This can be rearranged
as $l - 3w = 2$. We can easily solve this pair by substitution. From the first equation, we have $w = 18 - l$. Substituting this in the second equation, we can solve for $l$ first and then
for $w$: \begin{eqnarray} l - 3(18 - l) &=& 2\\ l - 54 + 3l &=& 2\\ 4l &=& 56\\ l &=& 14\\ 3w + 2 &=& 14\\ 3w &=& 12\\ w &=& 4\\ \end{eqnarray}
Answer: Length of the rectangle is 14 metres and its width is 4 metres.
The sum of the digits of a two digit number is 5. If the digits are reversed, the new number is reduced by 27. Find the number.
Solution:
Let the units digit and the tens digit of the two-digit number be $x$ and $y$ respectively. Then, the number is $10x + y$. Now, according to the first
information given, we have $x + y = 5$. If the digits are reversed, the number becomes $10y + x$. According to the given information, this number is 27 less than the original
number. So, we have the second equation: $$10y + x = 10x + y - 27$$. Rewriting this equation so that $x$ and $y$ terms are on the left side, we get $$- 9x + 9y = - 27$$. Dividing
this equation by $-9$ gives the equation in a simpler form: $$x - y = 3$$. Now, we can solve this pair of equations by elimination process: \begin{eqnarray} x + y &=& 5\\ x - y &=&
3\\ 2x &=& 8\\ x &=& 4\\ 4 + y &=& 5\\ y &=& 1\\ \end{eqnarray}
Answer: The required number is $41$.
To use a computer database, the charge is Rs.50 per hour during the day and Rs.35 per hour during night. If a research student paid Rs.740 for 16 hours of use, find the number of hours he worked on the database during daytime.
Solution:
Let the number of hours the research student worked during daytime be $x$ and the number of hours he worked at night be $y$. He has worked a total of
16 hours. This gives us the first equation $x + y = 16$. According to the given charges for daytime and nighttime usage, we get the second equation $50x + 35y = 740$.
Substitutine $y = 16 - x$ from the first equation into the second equation and solving for $x$ gives the required answer: \begin{eqnarray} 50x + 35(16 - x) &=& 740\\
50 x + 560 - 35x &=& 740\\ 15x &=& 180\\ x &=& 12\\ \end{eqnarray}
Note that we don't need to find the value $y$ as the night time hours is not asked. Nevertheless, we can get it by substituting $x = 12$ in the first equation: $12 + y = 16 \implies y = 4$
Answer: The research student worked $12$ hours during day time.
Two cars are100 miles apart. They start driving at the same time. If they drive towards each other they will meet in 1 hour. If they drive in the same direction, they will meet in 2 hours. Find their speeds.
Solution:
We do this problem using the basic distance-speed formula $t = \frac{d}{s}$. where $d$ is the distance covered, $s$ is the speed, and $t$ is the time taken.
Let the speed of car A be $x$ miles per hour and the speed of car B be $y$ miles per hour. If they drive towards each other, they will meet somewhere in between, shown by the
figure.
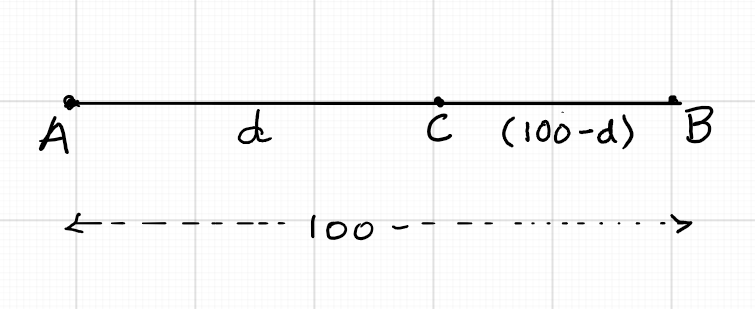
If car A covers $d$ miles when they meet, then car B would cover $(100 - d)$ miles. But both of them would have travelled for $1$ hour, as they meet in 1 hour. So, we have:
\begin{eqnarray} \frac{d}{x} =\frac{100-d}{y} &=& 1\\ \frac{d}{x} &=& 1 \implies d = x\\ \frac{100 - d}{y} &=& 1\\ \frac{100 - x}{y} &=& 1\\ y &=& 100 - x\\ x + y &=& 100\\ \end{eqnarray}
Thus, we have our first linear equation $x + y = 100$. For the second equation, we consider the second situation, where both cars travel in the same direction. Then, they will meet
at a point on the side of the slower car. Let them meet at the point C, $d$ miles on the side of car B, as shown in the figure:
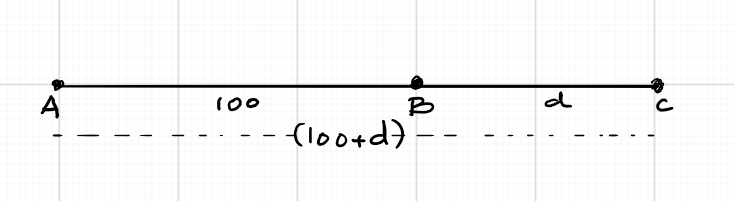
Now, when they meet at C, car A would have travelled $100 + d$ miles whereas car B would have travelled $d$ miles. As they meet in 2 hours, both
cars would have travelled for 2 hours. Hence we have: \begin{eqnarray} \frac{100 + d}{x} = \frac{d}{y} &=& 2\\ \frac{d}{y} &=& 2 \implies d = 2y\\
\frac{100 + d}{x} &=& 2\\ \frac{100 + 2y} {x} &=& 2\\ 2x &=& 100 + 2y\\ 2x - 2y &=& 100\\ x - y &=& 50\\ \end{eqnarray}
Now we have the second equation $x - y = 50$. Adding the two equations eliminates $y$ so we can solve for $x$. Then, substituting the value of $x$
in first or second equation produces the value for $y$: \begin{eqnarray} x + y &=& 100\\ x - y &=& 50\\ 2x &=&150\\ x &=& 75\\ 75 + y &=& 100\\
y &=& 25\\ \end{eqnarray}
Answer: Speed of the faster car A if $75$ miles per hour and speed of the slower car B is $25$ miles per hour.
Five years ago, Ram was seven times as old as his son. Five years hence, he will be four times as old as his son. Find their present ages.
Solution:
Let Ram's present age be $x$ years and his son's present age be $y$ years.
Five years ago, Ram was $(x - 5)$ years old and his son was $(y - 5)$ years old. So, according to the given information, we have: \begin{eqnarray}
x - 5 &=& 7(y - 5)\\ x - 5 &=& 7y - 35\\ x - 7y &=& - 30\\ \end{eqnarray}
Five years hence, Ram will be $(x + 5)$ years old and his son will be $(y + 5)$ years old. According to the given information, we have:
\begin{eqnarray} x + 5 &=& 4(y + 5)\\ x + 5 &=& 4y + 20\\ x - 4y &=& 15\\ \end{eqnarray}
We can eliminate $x$ by multiplying first equation by $(-1)$ and adding to the second. Then, substituting the value of $x$ in one of the equations would
give the value of $y$: \begin{eqnarray} -x + 7y &=& 30\\ x - 4y &=& 15\\ 3y &=& 45\\ y &=& 15\\ x - 4(15) &=& 15\\ x - 60 &=& 15\\ x &=& 75\\ \end{eqnarray}
Answer: Ram's present age is 75 years and his son's present age is 15 years.
A man can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find his speed of rowing in still water and the speed of the current in the stream.
Solution:
Let the man's speed of rowing in still water be $x$ km/h and the speed of the current be $y$ km/h. When he rows downstream,
speed of the boat increases to the extent of the speed of the current. So, his speed would be $(x + y)$ km/h. He covers 20 km in 2 hours. So, his speed
downstream is $\frac{20}{2} = 10$ km/h. This gives us the first equation $x + y = 10$.
When he rows upstream, his speed decreases to the extent of the speed of the current. So, his speed is $(x - y)$ km/h. He covers 4 km in 2 hours downstream.
So, his speed downstream is $\frac{4}{2} = 2$ km/h. This gives us the second equation $x - y = 2$. Adding the two equations results in cancelling $y$
and solving for $x$. Substituting the value of $x$ in one of the equations gives us the value of $y$. \begin{eqnarray} x + y &=& 10\\x - y &=& 2\\
2x &=& 12\\ x &=& 6\\ 6 + y &=& 10\\ y &=& 4\\ \end{eqnarray}
Answer: The man's rowing speed is 6 km/h and speed of the current is 4 km/h.
A total of 750 tickets were sold. 500 tickets of Rs. 10, and 250 tickets of Rs.15.
Onc burger costs Rs.40 and one pepsi cost Rs.15.
$x = 2$; $y = 3$; Area = 180 sq. units.
He covered 12 km by cycle and 8 km by walk.
he collected 19 coins of 10p denomination and 11 coins of 20p denomination.
The fraction is $\frac{5}{12}$
Dimensions of the two triangles are 5 cm. x 9 cm. x 9 cm. and 5 cm. x 18 cm. x 18 cm.
Fixed rate of Rs.28 for the first minute, and Rs.12 for each additional minute.
Rs. 30,000 to be invested in stocks and Rs. 50,000 to be invested in the bonds.
The plumber worked for 6 hours and the apprentice worked for 3 hours.
He got 3 notes of Rs.500 and 12 notes of Rs.200.
Each bought 9 shirts and 12 sarees.
He stacks 12 boxes of capacity 20 tons and 18 boxes of capacity 15 tons.r
Ravi walked at a speed of 4 km/hr and the speed of the taxis were 18 km/hr, on both days.
Air speed of the airplane is 105 miles per hour and wind speed is 15 miles per hour.