Dr. Lalitha Subramanian, About the Author
CBSE X Mathematics
CHAPTER 2: Polynimials
2-1: Zeros of a Polynomial
We have studied inprevious classes about polynomials in one variable. We recall the important aspects below:
- Standard form of writing a polynomial of one variable is $p(x) = a_{n}x^n + a_{n-1}x^{n-1} + ...... a_{2}x^2 + a_{1}x + a_{0}$ where $a_{n} \neq 0$.
- Degree of the highest degree term in the polynomial is the degree of the polynomial.
- If $k$ is any real number, then the value obtained by substituting $x = k$ in the polynomial is called the value of the polynomial at $x = k$ and denoted by $p(k)$.
- If $p(k) = 0$ for some real number $k$, then $k$ is said to be the zero of the polynomial..
A polynomial of degree $1$ is called a linear polynomial. Standard form of a linear polynomial is $p(x) = ax + b$. Examples
of a linear polynomial are $p(x) = 2x + 3$, $p(x) = -5x + \frac{2}{3}$, $p(x) = 2x$, etc. A linear polynomial has at most two terms.
A polynomial of degree $2$ is called a quadratic polynomial . Standard form of a quadratic polynomial is $p(x) = ax^2 + bx + c$.
Examples include $p(x) = 2x^2 -7x + 4$, $p(x) = -x^2 + 4x$, $p(x) = 4x^2 - 9$, etc. A quadratic polynomal as at most three terms.
A cubic polynomial is one with degree $3$. Standard form of a cubic polynomial is $p(x) = ax^3 + bx^2 + cx + d$. Examples of cubic polynomial
include $p(x) = 2x^3 + 5x^2 - x + 8$, $p(x) = -x^3 + 4x^2 + 6$, $p(x) = 4x^3 + x - 10$, $p(x) = -5x^3 + 7x^2 + x$, etc. A cubic polynomial
has at most four terms.
In general, a polynomial of $n$ degree has at most $n+1$ terms.
Zeros of the polynomial can be obtained by setting $p(x) = 0$ and solving for $x$. For example, the zero of a linear polynomial $p(x) = 2x - 1$ is obtained by setting $2x - 1 = 0$, which gives $x = \frac{1}{2}$. In general zero of a linear polynomial $p(x) = ax + b$ is $x = -\frac{b}{a}$.
Geometrically, zero of a polynomial is the point where the graph of the polynomial $y = p(x)$ intersects the $x$-axis, which is also called the $x$- intercept. A polynomial of degree $n$ has at most $n$ $x$-intercepts.
Example 1:
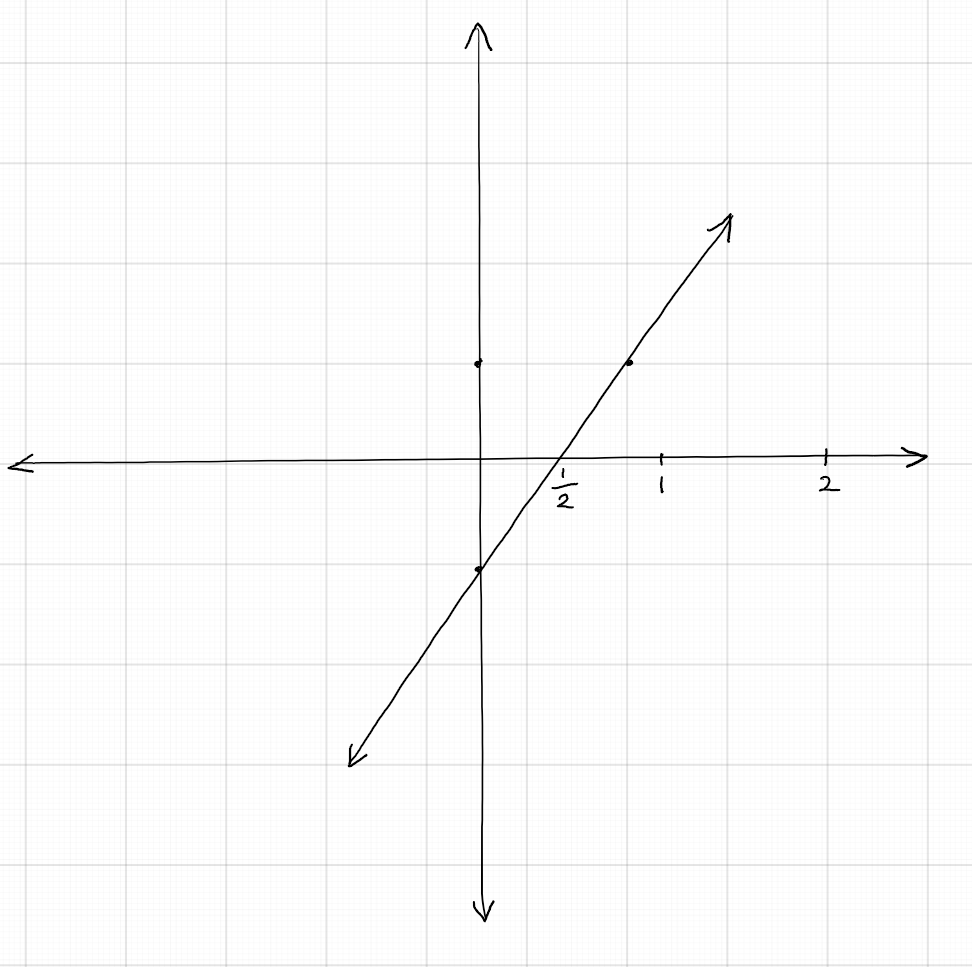
Graph the linear polynomial $2x - 1$ and show the $x$- intercept. Verify that the zero of this polynomial is the $x$-intercept.
Solution:
The table below gives the values of $y$ for which $y = 2x -1 $ . As two distinct points determine a unique line, it is sufficient to
determine the coordinates of two points on this line.
\begin{array}{ccc} x & y=2x-1 & (x,y)\\ \hline 0 & -1 & (0,-1)\\ 1 & 1 & (1,1)\\ \hline \end{array}
The graph shows the line $y = 2x - 1$. From the graph, it is clear that the line intersects the
$x$-axis at the point $(\frac{1}{2}, 0)$. Algebraically, we can solve the equation $2x - 1 = 0$ to get $x = \frac{1}{2}$, thus verifying that the zero of
this polynomial is the $x$-intercept.
In general, a linear polynomial has at most $1$ zero. This means that the graph has either $0$ or $1$ $x$-intercept. The example above shows the graph of a line that has $1$ $x$-intercept. The graph of a linear polynomial $y = ax + b$ is a rising line (going upward) is the leading coefficient $a \gt 0$ and a falling line (going downward) if the leading coefficient $a \lt 0$. A horizontal line has $0$ $x$-intercept. Equation of this line is $y = 0$. That is, it is a $0$ polynomial.
A quadratic polynomial has at most two zeros. That is, it can have $0$, $1$, or $2$ zeros. Geometrically, this means that the graph of a quadratic polynomial may have $0$, $1$, or $2$ $x$-intercepts. Algebraically, the zeros are obtained by solving the equation $ax^2 + bx + c = 0$. The following graphs are graphs of a quadratic polynomial with $0$, $1$, or $2$ zeros. Note that the graph is 'U' shaped, and opens upwards if the leading coefficient $a \gt 0$, and opens downwads when $a \lt 0$.
.png)
.png)
.png)
A cubic polynomial has at most 3 zeros. That is, the graph of a cubic polynomial has $0$, $1$, $2$, or $3$ x-intercepts. The graph of a cubic polynomial starts going upward (rising) and takes 2 turns if the leading coefficient $a \gt 0$ and starts going downward (falling) and then takes two turns if $a \lt 0$. Following graphs illustrate this property.
.png)
.png)
.png)
.png)
Practice Problems
Observe each of the graph given below and determine the number of distinct zeros of the polynomial whose graph is given.
$3$
$3$
$2$
$4$
$6$
2-2: Relationship Between the Zeros and Coefficients of a Polynomial
Consider a linear polynomial $p(x) = 2x + 5$. Then, its zero is obtained by setting $p(x) = 0$. That is, $2x + 5 = 0$. This gives $x = -\frac{5}{2}$. In general, zero of a linear polynomial $p(x) = ax+ b$ is $x = -\frac{b}{a}$, where $a$ is the coefficient of $x$ and $b$ is the constant term.
Example 1:
Find the zero of each of the following linear polynnomials: $(i) p(x) = 4x - 8 \quad (ii) p(x) = -3x + 1 \quad (iii) p(x) = 4x + 3$ without algebraically solving.
Solution:
$(i)$ In this problem, $a = 4$ and $b = -8$. So, if $\alpha$ is the zero of the polynomial, then, $\alpha =-\frac{-8}{4} = 2$
$(ii)$ Here, $a = -3$ and $b = 1$. So, the zero $\alpha = -\frac{1}{-3} = \frac{1}{3}$.
$(iii)$ Here, $a = 4$ and $b = 3$.
So. the zero $\alpha = -\frac{4}{3}$
To understand the relationship between the zeroes and the coefficients of quadratic polynimials, we shall consider an example.
Example 2:
Find the zeroes of the quadratic polynomial $p(x) = 2x^2 - 5x + 3$
Solution:
Zeroes of this polynomial can be obtained by solving the equation $2x^2 - 5x + 3 = 0$. By the known factorizing method, we have product of the two zeroes
$+6$ and sum $-5$. \begin{eqnarray} 2x^2 - 5x + 3 &=& 0\\ 2x^2 - 3x - 2x + 3 &=& 0\\ x(2x - 3) - 1(2x - 3) &=& 0\\ (x - 1)(2x - 3) &=& 0\\ \end{eqnarray}
zeroes of the polynomial are obtained by setting each factor to zero. If $\alpha$ and $\beta$ are the zeroes, then we have $\alpha = 1$ and $\beta = \frac{3}{2}$. Now,
sum of the zeroes $\alpha + \beta = 1 + \frac{3}{2} = \frac{5}{2}$. Note that $-5$ is the coefficient of $x$ and $2$ is the coefficient of $x^2.$ Product of the zeroes $\alpha \beta = 1 \times \frac{3}{2} = \frac{3}{2}$. Note that the numerator $3$ is the constant term and the denominator $2$ is the coefficient of $x^2$.
Standard form of a quadratic polynomial is $p(x) = ax^2 + bx + c$. In general, if $\alpha$ and $\beta$ are the zeroes of this polynomial, then, the sum of the zeroes $\alpha + \beta = -\frac{b}{a}$, where $b$ is the coefficient of the $x$ term and $a$ is the coefficient of the $x^2$ term, i.e., the leading coefficient. Product of the zeroes $\alpha \beta = \frac{c}{a}$, where $c$ is the constant term and $a$ is the leading coefficient.
Example 2:
Find the zeroes of the polynomial $x^2 - 6x + 8$ and verify the relationship between the zeroes and the coefficients of the polynomial.
Solution:
First, let us solve the equation $x^2 - 6x + 8 = 0$ to find the zeroes: \begin{eqnarray} x^2 - 6x + 8 &=& 0\\ x^2 - 4x - 2x + 8 &=& 0\\ x(x - 4) -2(x - 4) &=& 0\\
(x - 4)(x - 2) &=& 0\\ \end{eqnarray}
Sum of the zeroes = $4 + 2 = 6 = \frac{6}{1}$. Coefficient of $x$ is $-6$ and coefficient of $x^2$ is $1$.
Product of the zeroes is $(4)(2) = 8 = \frac{8}{1}.$ Constant term is $8$ and coefficient of $x^2$ is $1$. Thus the relationship is verified.
Example 3:
Find a quadratic polynomial such that the sum and product of its zeroes are $8$ and $15$ respectively.
Solution:
The standard form of a quadratic polynomial is $ax^2 + bx + c$. Let its zeroes be $\alpha$ and $\beta$. Then, according to the given information, $\alpha + \beta = -\frac{b}{a} = 8$ and $\alpha\beta = \frac{c}{a} = 15$. If $a = 1$, then, we get $b = - 8$ and $c = 15$. So, one polynomial is $x^2 - 8x + 15$. Generally, any quadratic polynomial of the form $k(x^2 - 8x + 15)$ would satisfy the given condition.
Standard form of a cubic polynomial is $p(x) = ax^3 + bx^2 + cx + d$. If $\alpha$, $\beta$, and $\gamma$ are zeroes of the cubic polynomial, then we have: \begin{eqnarray} \alpha + \beta + \gamma &=& -\frac{b}{a}\\ \alpha \beta + \beta \gamma + \alpha \gamma &=& \frac{c}{a}\\ \alpha \beta \gamma &=& -\frac{d}{a}\\ \end{eqnarray}
Example 4:
verify that $-1$, $2$, and $5$ are zeroes of the cubic polynomial $x^3 - 6x^2 + 3x + 10$. Then, verify the relationship between the zeroes and the coeffiients of the polynomial.
Solution:
Given that $-1$, $2$ and $5$ are zeroes of the cubic polynomial. This means that $x + 1$, $x - 2$, and $x - 5$ are factors of the polynomial. So, we need to
just verify whether the product of these three factors results in the given polynomial: \begin{eqnarray} (x+1)(x - 2)(x - 5) &=& (x + 1)(x^2 - 7x + 10)\\ &=& x^3 + x^2 - 7x^2
- 7x + 10x + 10\\ &=& x^3 - 6x^2 + 3x + 10\\ \end{eqnarray}
Thus, we verify that the given numbers are zeroes of the given polynomial. Now,
we verify the relationship between the zeroes and the coefficients: \begin{eqnarray} -1 + 2 + 5 &=& 6 = -\frac{b}{a}\\ (-1)(2) + (2 )(5) + (5)(-1) &=&
3 = \frac{c}{a}\\ (-1)(2)(5) &=& - 10 = -\frac{d}{a}\\ \end{eqnarray}
We also note that $a = 1$, $ = - 6$, $c = 3$, and $d = 10$, thus verifying
the relationship between the zeroes and the coefficients.
Example 5:
Find a cubic polynomial with leading coefficient $2$ that has $1$, $-3$, and $\frac{1}{2}$ as zeroes, using the relationship between the zeroes and the coefficients of the polynomial.
Solution:
Let us assume that $\alpha = 1$, $\beta = - 3$, and $\gamma = \frac{1}{2}$. Then, we have \begin{eqnarray} \alpha + \beta + \gamma
&=& 1 - 3 + \frac{1}{2}\\ &=& \frac{2 - 6 + 1}{2}\\ &=& -\frac{3}{2}\\ \alpha\beta + \beta\gamma + \gamma\alpha &=& (1)(-3) + (-3)(\frac{1}{2}) +
(\frac{1}{2})(1)\\ &=& -3 - \frac{3}{2} + \frac{1}{2}\\ &=& \frac{-6- 3 + 1}{2}\\ &=& -\frac{8}{2}\\ \alpha\beta\gamma &=& (1)(-3)(\frac{1}{2})\\ &=&
-\frac{3}{2}\\ \end{eqnarray}
Foom the above computation, we have \begin{eqnarray} \alpha + \beta + \gamma &=& -\frac{3}{2} = -\frac{b}{a}\\
\alpha\beta + \beta\gamma + \gamma\alpha &=& -\frac{8}{2} = \frac{c}{a}\\ \alpha\beta\gamma &=& -\frac{3}{2} = -\frac{d}{a}\\ \end{eqnarray}
If $a = 2$, then we have $b = 3$, $c = - 8$, and $ d = 3$. So, the required cubic polynomial is $2x^3 + 3x^2 - 8x + 3$.
Practice Problems
For problems #1- 5, verify the relationship between the zeroes and the coefficients of each of the given quadratic polynomials:
Zeroes are $-4$ and $-2$.
Zeros are $4$ and $-2$.
Zeroes are $1$ and $-4$.
Only one zero $-3$ with multiplicity $2$.
Zeroes are $1$ and $-\frac{7}{3}$
For problems # 6 - 10, find a quadratic polynomial that has the given zeros:
$x^2 + x - 20$
$x^2 - 2$
$2x^2 + 3x - 2$
$6x^2 - x - 2$
$4x^2 + 3x - 1$
For problems # 11 - 15, verify that the given numbers are the zeros of each of the cubic polynomial . Then verfiy the relationship between the zeroes and the coefficients:
To verify.
To verify
To verify
To verify
To verify
For problems # 16 - 20, find a cubic polynomial that has the given zeroes:
$x^3+ 5x^2 - 12x - 36$
$x^3 + x^2 - 12x$
$2x^2 + 5x^2- 22x + 15$
$x^3 - 2x^2 - 3x + 6$
$x^3 - 4x^2 + 5x - 2$
2-3: Division Algorithm fof Polynomials
The division algorithm for real numbers that we learnt in earlier section can be extended to polynomials. The statement is as follows:
If $A(x)$ and $B(x)$ are any two polynomials with $B(x) \neq 0$, Then, we can find two polynomials such that $A(x) = B(x) \times q(x) + r(x)$, where
the degree of $r(x)$ is less than the degree of $B(x)$, or $r(x) = 0$.
Basically this means that, when $A(x)$ is divided by $B(x)$, you get a quotient $q(x)$ and a remainder $r(x)$, then, the rule that
Dividend = Divisor x Quotient + Remainder.
Example 1:
Verify the division algorithm by dividing the polynomial $x^4 + 3x^3 - 3x^2 + 4x + 3$ by the polynomial $x^2 + x - 2$
Solution:
From the division process is shown below, we note that the quotient is $x^2 + 2x - 3$ and the remainder is $11x - 3$. According to the division
algorithm, Didivend = Divisor x Quotient + Remainder. We shall verify this as below: \begin{eqnarray} x^4 + 3x^3 - 3x^2 + 4x + 3 &=& (x^2 + x - 2)(x^2 + 2x - 3) + (11x - 3)\\
&=& x^4 + 2x^3 - 3x^2 + x^3+ 2x^2 - 3x - 2x^2 - 4x + 6 + 11x - 3\\ &=& x^4 + (2x^3 + x^3) + (-3x^2 + 2x^2 - 2x^2) + (-3x - 4x + 11x) + (6 - 3)\\ &=& x^4 3x^3 - 3x^2 + 4x + 3\\ \end{eqnarray}
Thus, division algorithm is verified.
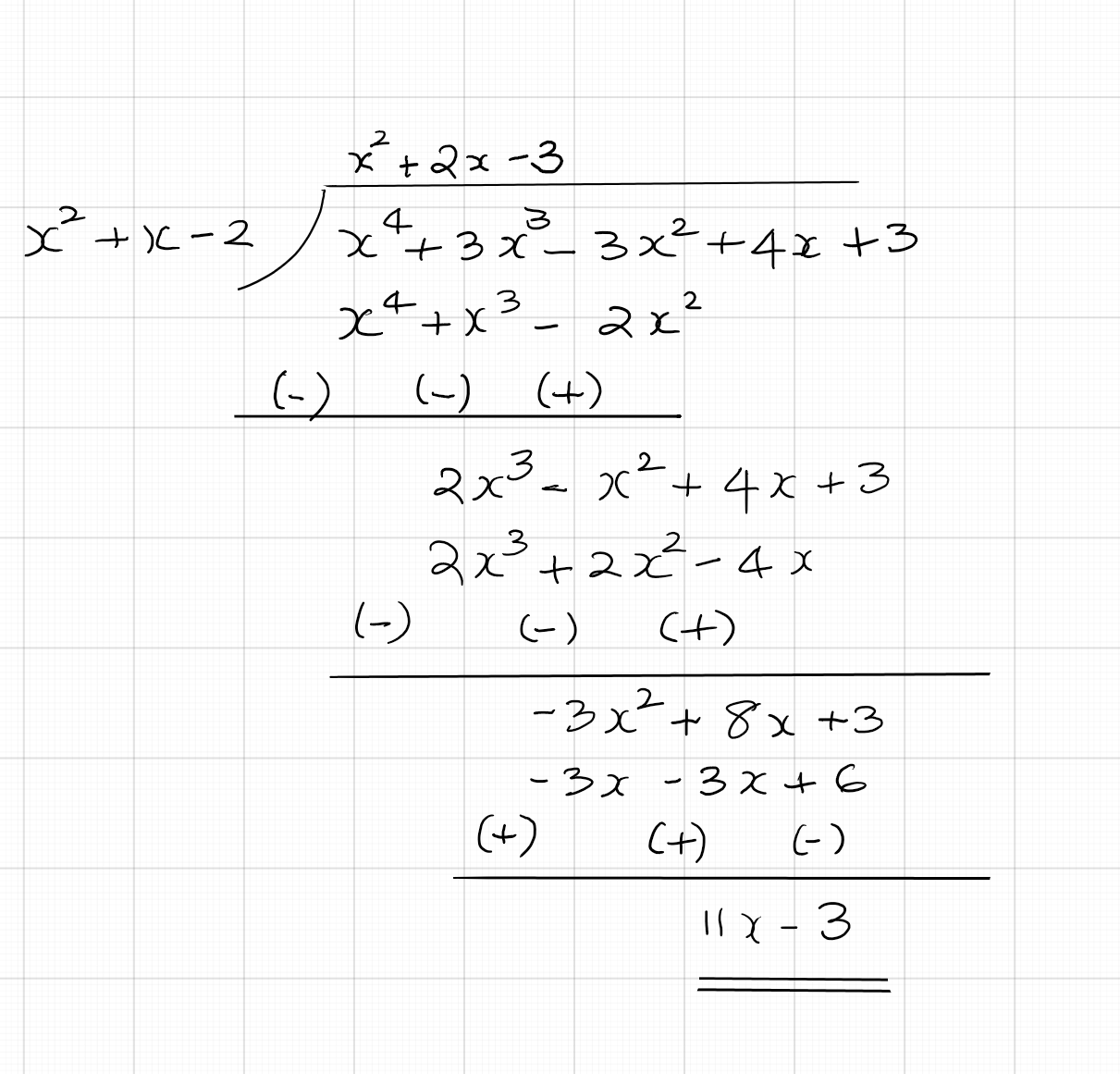
Division algorithm can be used to find the zeroes of a polynomial, is some of the zeroes are given, as illustrated in the following example.
Example 2:
Find all the zeroes of the polynomial $2x^4 + 2x^3 - 13x^2 - x + 6$, given that $\frac{1}{\sqrt{2}}$ and $-\frac{1}{\sqrt{2}}$ are two of the zeroes.
Solution:
Since $\frac{1}{\sqrt{2}}$ and $-\frac{1}{\sqrt{2}}$ are zeroes of the polynomial, $\left(x - \frac{1}{\sqrt{2}}\right)\left(x + \frac{1}{\sqrt{2}}\right) =
x^2 - \frac{1}{2}$ is a factor of the polynomial. That is, $\frac{1}{2}(x^2 - 1)$ is a factor. Now, we divide the given polynomial by $x^2 - 1$ as shown below:
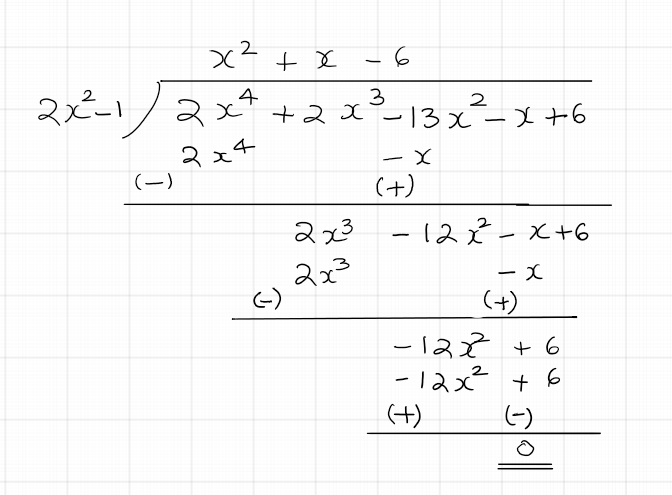
From the division shown above, we have quotient = $x^2 + x - 6$. As the divisor is a factor of the dividend, we get the remainder $0$. Factorizing the quotient, we get $x^2 + x - 6 = (x - 2)(x + 3)$. Setting each of these factors to zero gives us the other two zeroes of the polynomial as $2$ and $-3$. So, the zeroes of the given polynomial are $2$, $-3$, $\frac{1}{\sqrt{2}}$ and $-\frac{1}{\sqrt{2}}$
The example below shows use of division algorithm in solving another type of problem:
Example 3:
On dividing the polynomial $x^4 - 2x^3 + x^2 + 3x - 8$ by a polynomial $g(x)$, the quotient is $x^2 - 4x + 12$ and the remainder is $-33x + 28$. Find $g(x)$.
Solution:
Using the division algorithm and substituting for the dividend, quotient, and remainder, we can solve for the divisor $g(x)$. We have $x^4 - 2x^3 + x^2 + 3x - 8 = (x^2 - 4x + 12)[g(x)] + (-33x + 28)$. Subtracting the remainder from both sides gives $x^4 - 2x^3 + x^2 + 36x - 36$. This means that $x^2 - 4x + 12$ and $g(x)$ are factors of the given polynomial. Hence, we can get $g(x)$ by dividing the given polynomial by $x^2 - 4x + 12 $:
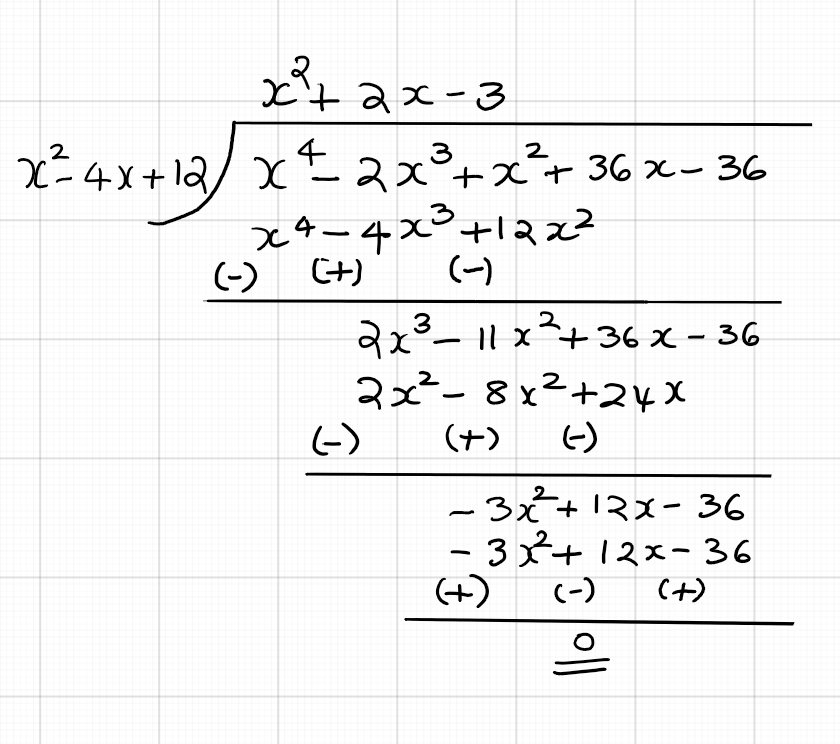
Practice Problems
For problems # 1 - 4, divide each polynomial $p(x)$ by the polynomial $d(x)$ and find the quotient and remainder .
Quotient is $x^2$ and remainder is $5$.
Quotient is $x - 6$ and remainder is $-6x + 2$
Quotient is $x + 2$ and remainder is $-x + 11$.
Quotient is $x^2 + x + 1$ and remainder is $2x + 9$.
No. Because, we get a non-zero remainder upon division.
Yes. we get a zero remainder upon division.
$-4$
$3$ and $1$ are the other zeroes.
$d(x) = x^2 - 2x + 3$.
$d(x) = x^2 + x - 2$