Precalculus

while drawing the diagram, interpretations of the following phrases should be kept in mind:

Example 1:

From a point $340$ feet away from the base of a building, the angle of elevation to the top of a building is $65^0$. Find the height of the building.

Solution:
043P_E1

The diagram shown above is a mathematical model of the problem. Here AB represents the building and the point C represents the point from which observation is made. From the right triangle form, we have: \begin{eqnarray} \tan 65^0 &=& \frac{h}{340}\\ h &=& 340 \tan 65^0\\ h &\approx& 729' \\ \end{eqnarray}

Example 2:

A person standing at the top of a tower $205$ feet tall observes his friend coming towards the tower at an angle of depression of $75^0$. How are is his friend from the base of the tower at that time?

Solution
043P_E2

The above diagram shows the Tower AB of height $205$ feet, the persone standing at the top as the point B, and the friend as point C. The angle from B's horizontal line of vision, downwards, to his actual line of vision is $75^0$. This is equal to $\angle{ABC}$, due to alternate angles property of parallel lines. Let the distance of $C$ from the base of the tower $A$ be $x$. Then, we have: \begin{eqnarray} \tan 75^0 &=& \frac{205}{x}\\ x &=& \frac{205}{ \tan75^0}\\ x &\approx& 55\\ \end{eqnarray}

Example 3:

From a telescope placed on top of a 5-feet tripod, an observer measures an angle of elevation of $8^0$ to the top of a tree that is $120$ feet away. How tall is the tree?

Solution:

In the above diagram, AB is the tripod in which B is the telescope. CD is the tree. We have the $BE = AC = 120$ and $CE = AB = 5$ as opposite sides of a rectangle are equal. Let $DE = x$. Then, we have \begin{eqnarray} \tan 8^0 &=& \frac{x}{120}\\ x &=& 120 \tan 8^0\\ x &\approx& 16.9\\ DC &=& DE + EC\\ DC &\approx& x + 16.9\\ DE &\approx& 21.9\\ \end{eqnarray}

Example 4:

A person standing on the deck of a ship observes a hill-top in an island at an angle of elevation of $35^0$. After the ship has moved 900 feet, closer to the island, the angle of elevation becomes $42^0$. What is the height of the hill above sea-level?

Solution:
043P_E4

In the above diagram, The point $A$ represents the person on the ship. BC is the hill on the island. The point $D$ represents the position of the ship after it has moved $900$ feet closer to the island. Here we have two unknown quantities, namely, DB and BC. Let $DB = x$ and $BC = h$. In triangle DBC, we have \begin{eqnarray} \tan 42^0 &=& \frac{h}{x}\\ h &=& x(\tan42^0)\\ h &\approx& 0.9004x\\ \end{eqnarray}

In triangle ABC we have: \begin{eqnarray} \tan 35^0 &=& \frac{h}{(900+x)}\\ 0.7002 &\approx& \frac{0.9004x}{900+x}\\ 0.7002(900+x) &\approx& 0.9004x\\ 0.7002 + 630.18 &\approx& 0.9004x\\ 630.18 &\approx& 0.2002x\\ 3146.9 &\approx& x\\ h &\approx& 0.9004x\\ h &\approx& 2833.47\\ \end{eqnarray}

Example 5:

A tall tower in a certain city casts a shadow approximately $120$ feet long on the street when the angle of elevation of Sun's rays at the top of the tower is $74^0$. How tall is the tower?

Solution:
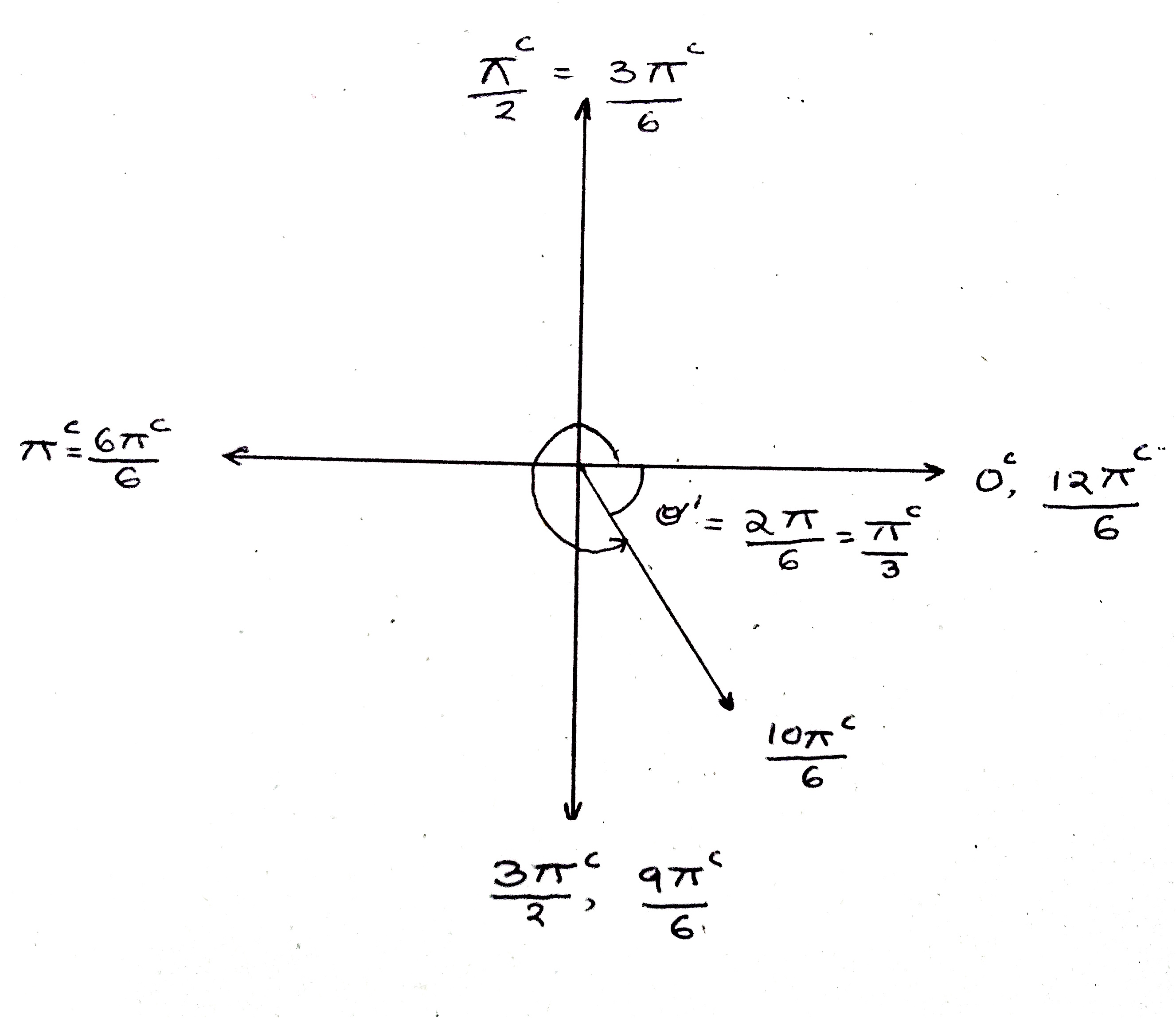
043P_E5

Based on the above diagram, we have: \begin{eqnarray} \tan74^0 &=& \frac{h}{120}\\ h &=& 120 \times \tan74^0\\ h &\approx& 419\\ \end{eqnarray}.

Example 6:

The height of an isosceles trapezoid is 8 units and the bases have lengths 7 units and 15 units. Find the measures of its angles.

Solution:
043P_E6

Above diagram shows the isosceles trapezoid $ABCD$, with heights $AE = BF = 8$. From the basic property of isosceles trapezoid, we have $DE = FC = 4$. In triangle $ADE$, \begin{eqnarray} \tan \theta &=& \frac{8}{4}\\ \theta &\approx& 63.4^0\\ \end{eqnarray}

The two acute base angles are approximately $63.4^0$ and the two top obtuse angles are $116.6^0$.

Example 7:

For the regular pentagon $ABCDE$ inscribed in a circle, the central angle $\angle AOB = \frac{360}{5} = 72^0$. If we draw a perpendicular $AP$ to side $AB$ of the isosceles triangle $AOB$, $\angle POB = 36^0$. Now, in the triangle $APB$, let $OP = x$. Then, we have \begin{eqnarray} \sin 36^0 &=& \frac{x}{4}\\ x &=& 4\sin36^0\\ x &\approx& 2.35\\ \end{eqnarray}.

Side $AB$ = twice of segment $BP$. If $P$ represents the perimeter of the pentagon, we have: \begin{eqnarray} AB &\approx& 2(2.35)\\ AB &\approx& 4.7\\ P &\approx& 5(4.7)\\ P &\approx& 23.5\\ \end{eqnarray}

Example 8:

In the above diagram, from right triangle $POB$,we have: \begin{eqnarray} \tan36^0 &=& \frac{x}{5}\\ x &=& 5\tan36^0\\ x &\approx& 3.63\\ AB &=& 2x\\ AB &\approx& 7.27\\ P &\approx& 36.33\\ \end{eqnarray}

Example 9:

A pendulum $40$ cm long is moved $22^0$ from its vertical position. How much is the lower end raised?

Solution:
043P_E9

In the above diagram, $AD$ is the vertical position of the pendulum. When its moves $22^0$, its new position is $AC$. We need to find $EC$, the extent to whcih its lower end is raised. Let $AB = x$. In triangle $ABC$, we have \begin{eqnarray} \cos22^0 &=& \frac{x}{40}\\ x &=& 40\cos22^0\\ x &\approx& 37.1\\ CE = BD &\approx& 2.9\\ \end{eqnarray}

Example 10:

The angles of elevations of a plane from two points on the ground, on either sides of the plane, are $$30^0$ and $42^0$ respectively. If the two points are $1200$ m apart, how high is the plane flying at that time?

Solution:

In the above diagram, points $P$, $A$, and $B$ are positions of the plane and the two points respectively. Draw perpendicular $PD$ from $P$ to $AB$. Let the height of the plane from the ground $PD = h$ and $AD = x$. Then, $DB = 1200-x$.
In triangle $PAD$, we have \begin{eqnarray} \tan42^0 &=& \frac{h}{x}\\ h &=& x\tan42^0\\ h &\approx& 0.9004x\\ \end{eqnarray}

Practice Problems

The acute angles of the rhombus are approximately $53^0$ each and the obtuse angles are approximately $127^0$ each.

Angle of elevation of the Sun from the tree-top is approximately $33.7^0$.

The ladder makes an angle of approximately $67.4^0$

The postman is approximately $88$ feet from the building.

The pilot would touch the runway approximately $16,485$ feet from the airport.

The kite is flying approximately at a height of $158$ feet.

Length of the yard is approximately $251.6$ m; Width of the yard is approximately $163.4$m.

The pendulum swing at an angle of $23^0$.

The height of the flagpole is about $64.5$m.

The pendulum is raised approximately $7$ cm.

At that time,the helicopter is flying at a height of approximately $1007$ m.

Height of the plane at that moment is approximately $1900$ feet; Horizontal distances of the nearest and the farthest ends of the strip are approximately $1700$ feet and $2800$ feet respectively.

Height of the tree is $19.8$ feet.

Length of the guy wire is approximately $193$ feet; Height of the tower is approximately $187$ feet.

During the time of observation,the car travels approximately $151$ feet.

The tree is approximately $32.8$ feet tall.

Distance of Q from P is approximately $3.12$ km.

Height of the tree is approximately $81$ feet.

The height of the building is approximately $36.6$ feet.

The height of the watch-stand is approximately $173.5$ feet.

The car is about $4581$ feet from the base of the tower.

The tree is about $41$ feet tall.

$545$ feet

The balloon is flying at a height of about 371 feet; The length of the rope is approximately $453$ feet.