Precalculus

Chapter 4: Trigonometric Functions

4.2: Trigonometric Functions of Acute Angles.

The fundamental concept of trigonometry is based on measurements involving right triangles and similarity of right triangles. Two right triangles are similar if one of the acute angles are equal. This means if, in two triangles $\Delta ABC$ and $\Delta PQR$, $\angle A = \angle P= 90^0$ and $\angle B = \angle Q$, Then $\Delta ABC \sim \Delta PQR$. Consequently, the corresponding sides are proportional. So, we get: $\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}$.

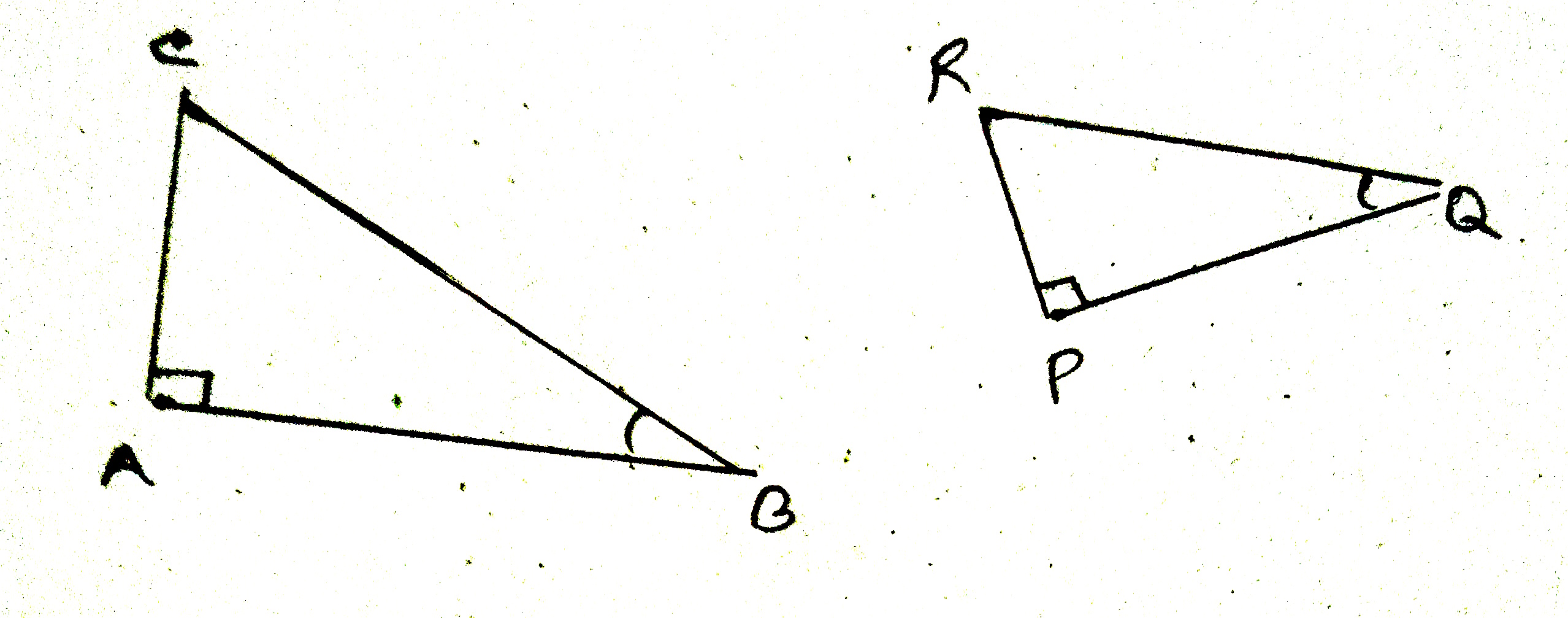
Generalizing this concept, it can be stated that all right triangles with a specific acute angle are similar, and hence, the ratios of any two corresponding sides are equal for all these similar triangles. This idea leads to the definitions of the basic trigonometric functions:

If we label the sides of opposite to the given acute angle $\theta$ as $O$, the hypotenuse as $H$, and the third side, which is adjacent to the given acute angle as $A$, then, we define the following ratios:

1. $\sin \theta = \frac{o}{h}$
2. $\cos \theta = \frac{a}{h}$
3. $\tan \theta = \frac{o}{a}$
4. $\csc \theta = \frac{h}{o}$.
5. $\sec \theta = \frac{h}{a}$.
6. $\cot \theta = \frac{a}{o}$.

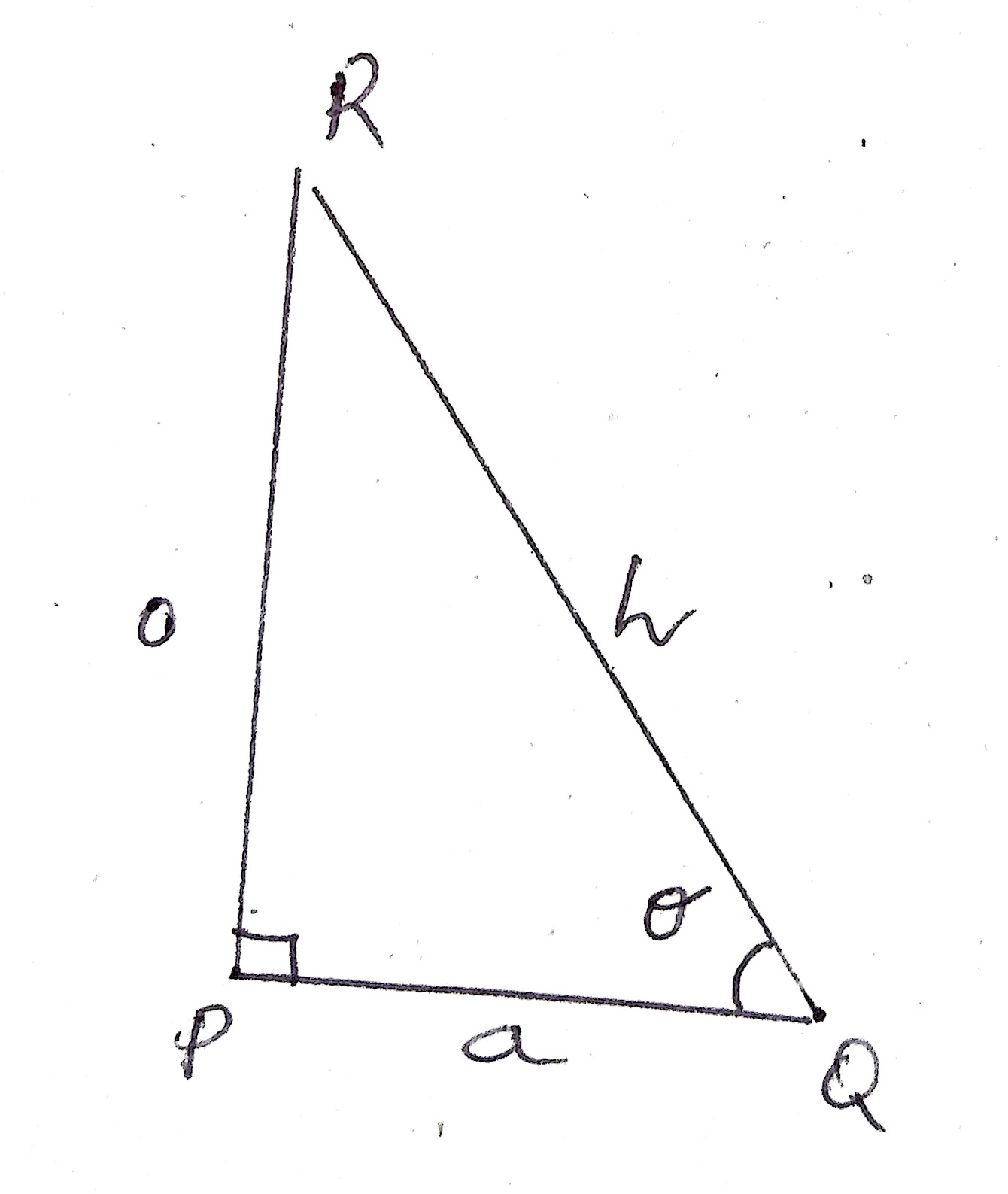
Obviously, the first three ratios are reciprocals of the next three ratios. Hence we get the following Reciprocal Identities:

1. $\sin \theta = \frac{1}{\csc \theta}$
2. $\cos \theta = \frac{1}{\sec \theta}$
3. $\tan \theta = \frac{1}{\cot \theta}$
4. $\csc \theta = \frac{1}{\sin \theta}$
5. $\sec \theta = \frac{1}{\cos \theta}$
6. $\cot \theta = \frac{1}{\cot \theta}$

Two special right triangles are of importance in trigonometry. Values of the trigonometric ratios of angles $30^0$, $45^0$, and $60^0$ can be evaluated using these triangles as follows:

Evaluating the trigonometric values for $30^0$, and $60^0$:

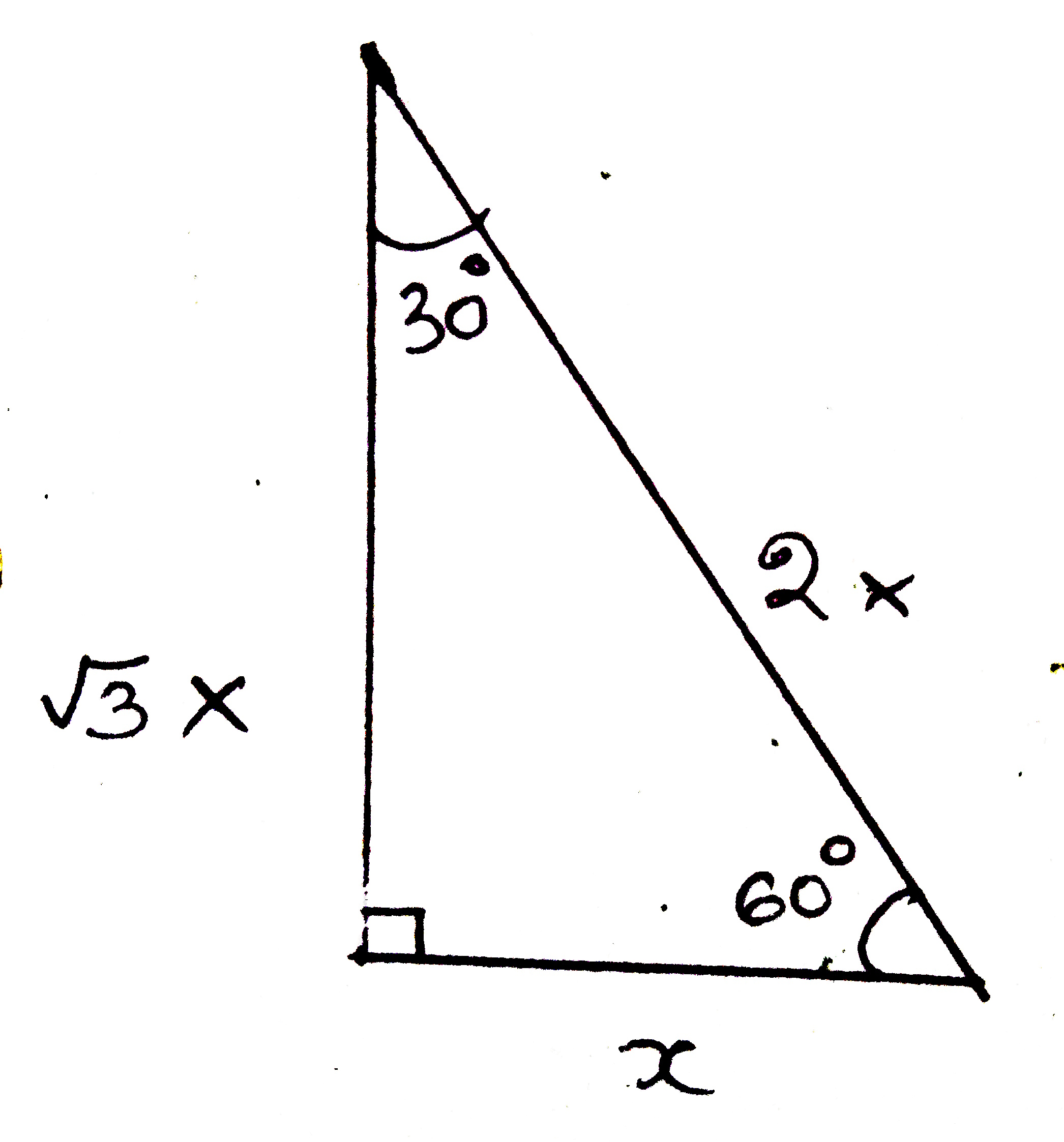
This special triangle is usually referred to as the $30^0-60^0-90^0$ triangle. Using Pythagorean Theorem, we deduce that the sides of this triangle are in the ratio $1:\sqrt{3}:2$. This means that, if the side opposite to $30^0$ is $x$ units, then, the side opposite to $60^0$ is $\sqrt{3}x$ units and the hypotenuse is $2x$ units. If we consider the angle $\theta$ to be $30^0$, then, adjacent side is $\sqrt{3}x$ units, opposite side is $x$ units, and hypotenuse is $2x$ units. So, the six trigonometric values for $30^0$ or $\frac{\pi}{6}^c$:

1. $\sin 30^0 = \frac{o}{h} = \frac{1}{2}$
2. $\cos 30^0 = \frac{a}{h} = \frac{\sqrt{3}}{2}$
3. $\tan 30^0 = \frac{o}{a} = \frac{1}{\sqrt{3}}$ or $\frac{\sqrt{3}}{3}$
4. $\csc 30^0 = \frac{h}{o} = 2$
5. $\sec 30^0 = \frac{h}{a} = \frac{2}{\sqrt{3}}$ or $\frac{2\sqrt{3}}{3}$
6. $\cot 30^0 = \frac{a}{o} = \sqrt{3}$

From this same triangles, we can evaluate trigonometric values of $60^0$ or $\frac{\pi}{3}^c$:

1. $\sin 60^0 = \frac{o}{h} = \frac{\sqrt{3}}{2}$
2. $\cos 60^0 = \frac{a}{h} = \frac{1}{2}$
3. $\tan 60^0 = \frac{o}{a} = \sqrt{3}$
4. $\csc 60^0 = \frac{h}{o} = \frac{2}{\sqrt{3}}$ or $\frac{2\sqrt{3}}{3}$
5. $\sec 60^0 = \frac{h}{a} = 2$.
6. $\cot 60^0 = \frac{a}{o} = \frac{1}{\sqrt{3}}$ or $\frac{\sqrt{3}}{3}$

The second special right triangle is the $45-45-90$ triangle. This is isosceles right triangle. So, by Pythagorean Theorem, is the two equal side are $x$ units, then the hypotenuse is $\sqrt{2}x$ units.

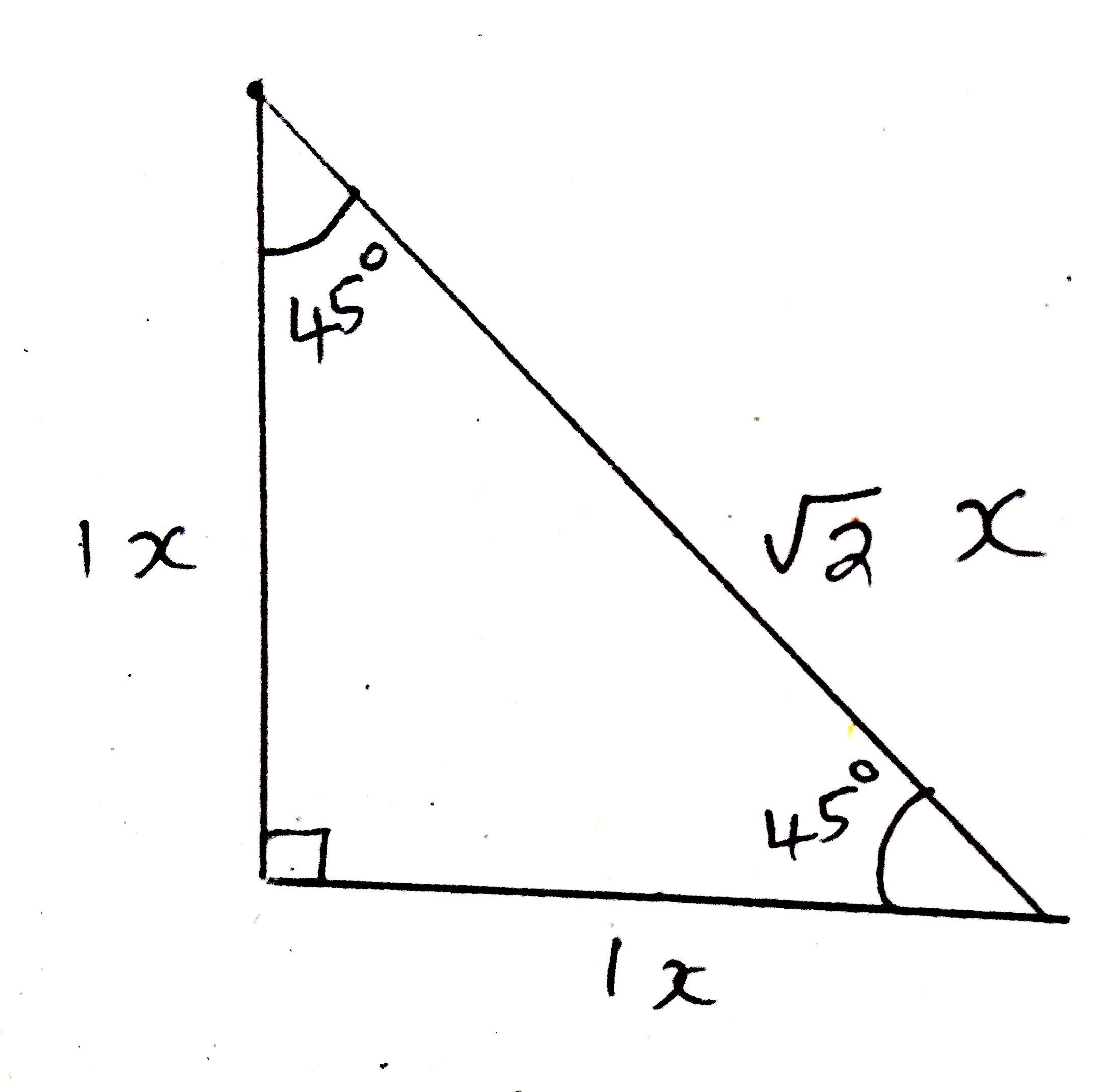
We note that the sides opposite the acute angles $45^0$ are $x$ units. So, we can evaluate the six trigonometric ratios for $45^0$ as under:

1. $\sin 45^0 = \frac{o}{h} = \frac{2}{\sqrt{2}}$ or $\frac{\sqrt{2}}{2}$
2. $\cos 45^0 = \frac{a}{h} = \frac{2}{\sqrt{2}}$ or $\frac{\sqrt{2}}{2}$
3. $\tan 45^0 = \frac{o}{a} = 1$
4. $\csc 45^0 = \frac{h}{o} = \sqrt{2} $.
5. $\sec 45^0 = \frac{h}{a} = \sqrt{2}$.
6. $\cot 60^0 = \frac{a}{o} = \frac{1}{\sqrt{3}}$ or $\frac{\sqrt{3}}{3}$

We note that $30^0$ and $60^0$ are complementary angles. Consequently, we also note that $\sin 30^0 = \cos 60^0$, $\sin 60^0 = \cos 30^0$. For this reason, the ratios $\sin \theta$ and $\cos \theta$ are called complementary ratios. Similarly we have $\tan \theta$ and $\cot \theta$ are complementary ratios, so also $\csc \theta$ and $\sec \theta$.

If one trigonometric ratio of a right triangle is given, we cen determine the other five ratios, using Pythagorean Theorem.

Example 1:

One acute angle of a right triangle is $\theta$. Given that $\sin \theta = \frac {3}{5}$, evaluate all other trigonometric ratios.

Solution:

First sketch a right triangle with $\theta$ as one acute angle. From the given information,label the given sides appropriately.

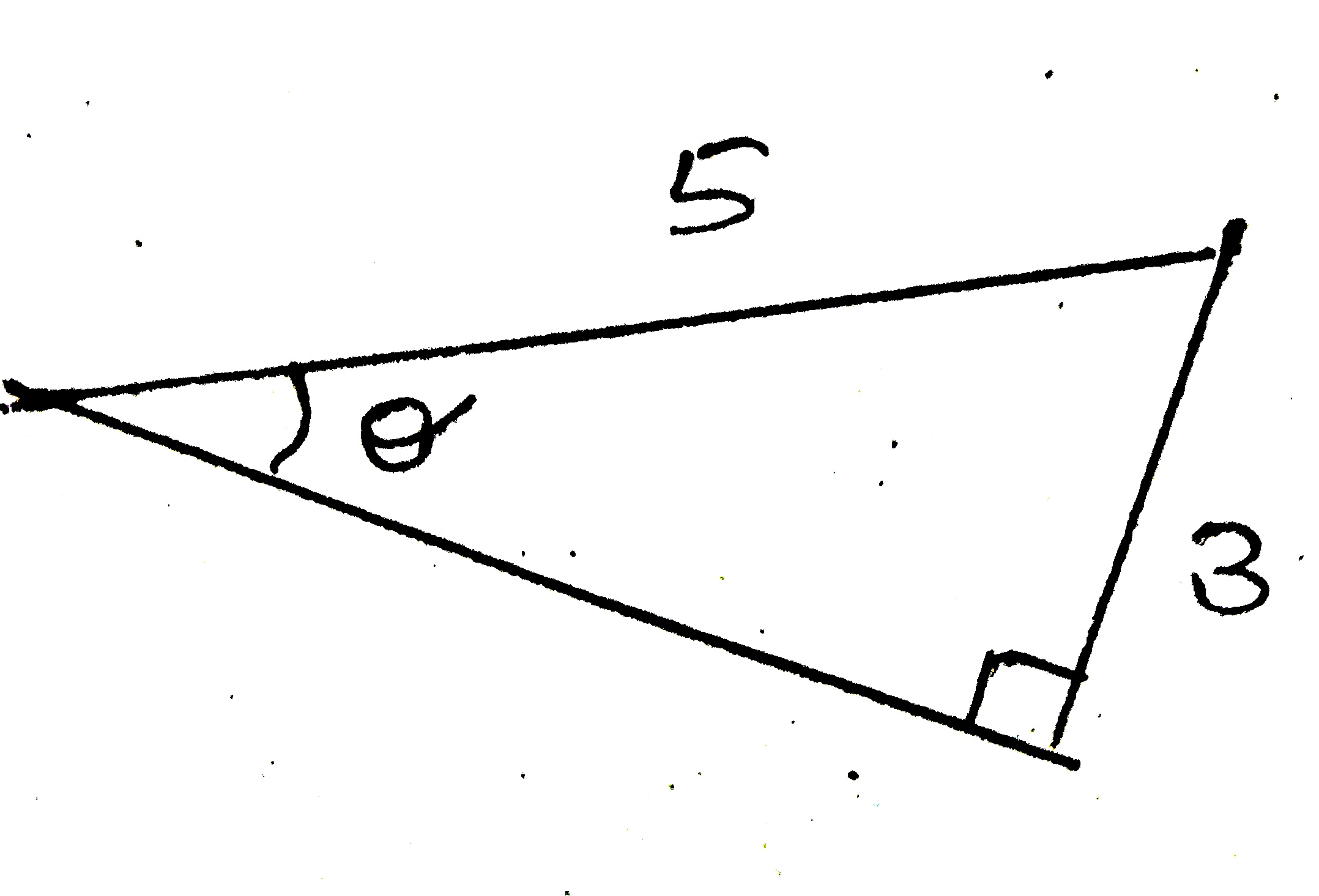
Using Pythagorean Theorem, we know that the adjacent side is $\sqrt{5^2 - 3^2} = 4$. Now, we can write values of the other five trigonometric ratios as under:

1. $\cos \theta = \frac{4}{5}$
2. $\tan \theta = \frac{3}{4}$
3. $\csc \theta = \frac{5}{3}$
4. $\sec \theta = \frac{5}{4}$
5. $\cot \theta = \frac{4}{3}$

Trigonometric values of angles other than the above-mentioned special angles angles are determined using a scientific calculator. We note that the calculator has keys for the $\sin\theta$, $\cos\theta$, and $\tan\theta$. Also, care must be taken to check whether the angle is given in degrees or radians. If it is given in DMS form, change it to decimal form before you put it in the calculator. The following precautions must be taken when using calculator to evaluate trigonometric functions.

1. Make sure that the mode is set to degrees or radians as per the requirement of the problem.
2. For evaluating the reciprocal functions $\csc\theta$, $\sec\theta$, and $\cot\theta$, input should be either $\frac{1}{\sin\theta}$ or $(\sin\theta)^{-1}$ for $\csc\theta$, etc.
3. If parentheses are used, make sure each parenthesis is closed, so that the calculator understand the order of operations required.

Example 2:

Evaluate the following using calculator:

$(a) \quad \sin(50^0)$
$(b) \quad \tan(84^0)$
$(c) \quad \sec(\frac{3\pi}{8}^c)$
$(d) \quad \csc(1.26^c)$

Solution:

$(a) \quad 0.7660$
$(b) \quad 9.5144$
$(c) \quad 2.6131$
$(d) \quad 1.0503$

Example 3:

A right triangle has hypotenuse of length $6$ units, and one of its acute angles as $40^0$. Find the measures of other two sides and the other acute angle.

Solution:

Sketch the triangle, marking the angles, and let the two arms of the triangle be $a$ and $b$.

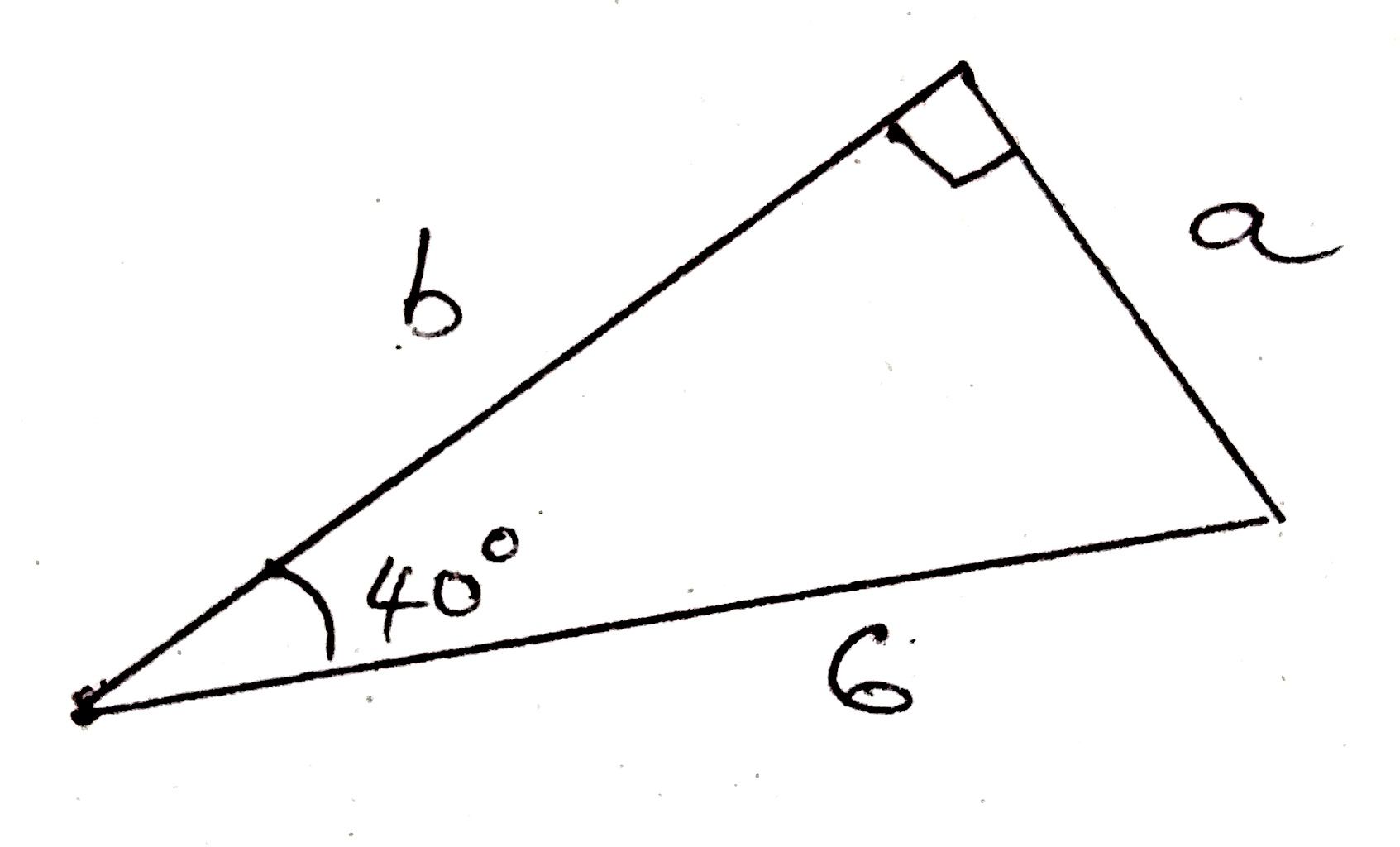
From the diagram, we can determine the values of $a$ and $b$: \begin{eqnarray} \sin 40^0 &=& \frac{a}{6}\\ a &=& 6\sin 40^0\\ a &\approx& 3.86\\ \cos 40^0 &=& \frac{b}{6}\\ b &=& 6\cos40^0\\ b &\approx& 4.6\\ \end{eqnarray}

Practice Problems

(1) Evaluate the six trigonometric ratios of $\theta$, based on the following diagram:

Hypotenuse = 25; $\sin\theta = \frac{24}{25}$; $\cos\theta = \frac{7}{25}$; $\tan\theta = \frac{24}{7}$; $\csc\theta = \frac{25}{24}$; $\sec\theta = \frac{25}{7}$; $\cot\theta = \frac{7}{24}$.

(2) Determine the lengths of the missing sides of the triangle shown below:

Let the hypotenuse be $a$ and the adjacent side be $b$. Then, $\sin30^0 = \frac{4}{a} \Rightarrow \frac{1}{2} = \frac{4}{a} \Rightarrow a=8$; $\cos30^0 = \frac{b}{a} \Rightarrow \frac{\sqrt{3}}{2} = \frac{b}{8} \Rightarrow b = 4\sqrt{3}$;

(3) Find the lengths of the missing sides of the triangle shown below:

Let the length of the side opposite to $45^0$ be $a$ and the length of the side adjacent be $b$. Then, we have $\sin45^0 = \frac{a}{8} \Rightarrow a = 4\sqrt{2}$; $\tan45^0 = \frac{a}{b} \Rightarrow 1 = \frac{a}{b} \Rightarrow b = 4\sqrt{2}$;

(4) Evaluate all the six trigonometric ratios of $\theta in the triangle shown below:

Length of the third side adjacent to $\theta$ is $6$. So, we have $\sin\theta = \frac{4}{5}$; $\cos\theta = \frac{3}{5}$; $\tan\theta = \frac{4}{3}$; $\csc\theta = \frac{5}{4}$; $\sec\theta = \frac{5}{3}$; $\cot\theta = \frac{3}{4}$.

(5) Evaluate $(a)$ $\sin\theta$, $(b)$ $\sec\theta$, and $(c)$ $\tan\theta$ in the triangle shown below:

Length of the side opposite to $\theta$ is $48$.
$(a)$ $\sin\theta = \frac{24}{25}$; $(b)$ $\sec\theta = \frac{25}{7}$; $(c)$ $\tan\theta = \frac{24}{7}$.

For problems # 6 - 10, evaluate the trigonometric functions other than the given function, for an acute angle $\theta$ of a right triangle.

(6) $\sin \theta = \frac{4}{5}$

$\cos \theta = \frac{3}{5}$; $\tan \theta = \frac{4}{3}$; $\csc \theta = \frac{5}{4}$; $\sec\theta = \frac{5}{3}$; $\cot \theta = \frac{3}{4}$

(7) $\tan \theta = \frac{24}{7}$

$\sin \theta = \frac{24}{25}$; $\cos \theta = \frac{7}{25}$; $\csc \theta = \frac{25}{24}$; $\sec \theta = \frac{25}{7}$; $\cot \theta = \frac{7}{24}$

(8) $\cos \theta = \frac{12}{13}$

$\sin \theta = \frac{5}{13}$; $\tan \theta = \frac{5}{12}$; $\csc \theta = \frac{13}{5}$; $\sec \theta = \frac{13}{12}$; $\cot \theta = \frac{12}{5}$

(9)$\sec\theta = \frac{17}{5}$

$\sin\theta = \frac{2\sqrt{66}}{17}$;$\cos\theta = \frac{5}{17}$; $\tan\theta = \frac{2\sqrt{66}}{5}$; $\csc\theta = \frac{17}{2\sqrt{66}}$; $\cot\theta = \frac{5}{2\sqrt{66}}$

(10) $\cot\theta = \frac{11}{\sqrt{23}}$

$\sin\theta = \frac{\sqrt{23}}{12}$; $\cos\theta = \frac{11}{12}$; $\tan\theta = \frac{\sqrt{23}}{11}$; $\csc\theta = \frac{12}{\sqrt{23}}$; $\sec\theta = \frac{12}{11}$

For problems #11 - 15, find the exact value of each without using a calculator.

(11) $\cos\frac{\pi}{4}$

$\frac{\sqrt{2}}{2}$

(12) $\sin\frac{\pi}{6}$

$\frac{1}{2}$

(13) $\tan45^0$

$1$

(14) $\sec\frac{\pi}{3}$

$2$

(15) $\cot30^0$

$\sqrt{3}$

For problems # 16-20, detrmine the values of the given functions, approximate to four decimal points.

(16) $\sin\frac{\pi}{12}$

$0.2588$

(17) $\tan40^024'$

$0.8511$

(18) $\sec19^0$.

$1.0576$

(19) $\csc\frac{\pi}{8}$.

$2.6131$

(20) $\cot1.24^c$

$0.3434$

For problems #21-24, Find the values of the acute angle that satisfies the given equation. give your exact answer in both degrees and in radians.

(21) $\cos\theta = \frac{\sqrt{2}}{2}$

$45^0$; $\frac{\pi}{4}^c$.

(22) $\csc\theta = 2$

$30^0$; $\frac{\pi}{6}^c$.

(23) $\tan\theta = \sqrt{3}$

$60^0$; $\frac{\pi}{3}^c$.

(24) $cot\theta = \sqrt{3}$

$30^0$; $\frac{\pi}{6}^c$.

In problems #25 - 28, solve for the variables shown in each diagram.

(25)

$z \approx 29.6$

(26)

$x \approx 45.68$

(27)

$y \approx 20.78$

(28)

$x \approx 27.16$.

(29) Solve the following triangle for unknown parts:

$c \approx 6.56$; $a \approx 7.55$; $ \theta \approx 49^0$

(30) Solve the triangle for unknown parts..

$q \approx 35.96$; $p \approx 33.79$; $\theta \approx 70^0$

(31) In a right triangle, an acute angle is $\theta = 37.5^0$ and the side opposite to $\theta$ has length $306$. How long is the side adjacent to $\theta$?

Approximately $398.797$.

(32) In a right triangle, an acute angle is $59^0$ and the side opposite to $\theta$ has length $117.42$. How long is the hypotenuse?

Approximately $136.99$.

(33) Find the value of the unique real number $\theta$ between $0$ and $2\pi$ that satisfies the conditions $\sin\theta -\frac{1}{2}$ and $\tan\theta \lt 0$..

$\sin\theta$ $\tan\theta$ are negative in QIV. Reference angle that satisfies the first condition is $\frac{\pi}{6}$. So, $\theta = 2\pi - \frac{\pi}{6} = \frac{11\pi}{6}$.

(34) If $\cos\theta = -\frac{5}{13}$ and $\tan\theta \gt 0$, find the value of $\sin\theta$.

$\cos\theta$ is negative and $\tan\theta$ is positive in QIII. Constructing the triangle in the third quadrant with the reference angle, we get the length of opposite side as $12$.
$\sin\theta = -\frac{12}{13}$.