Dr. Lalitha Subramanian
About the Author

Aksharam
A ray is a portion of a line, which has end point on one side and extends indefinitely on the other side. This end point is called the initial point or starting point.

An angle is the union of two non-collinear rays with a common starting point. This common starting point is called the vertex of the angle and the two rays are called the sides or legs of the angle. The interior of an angle is measured by the extent to which to two legs are apart from each other, at the vertex. Angles are measured in degrees and radians.
A degree is a measure equal to $\frac{1}{180}$th of a straight angle, represented by the symbol $^{0}$.
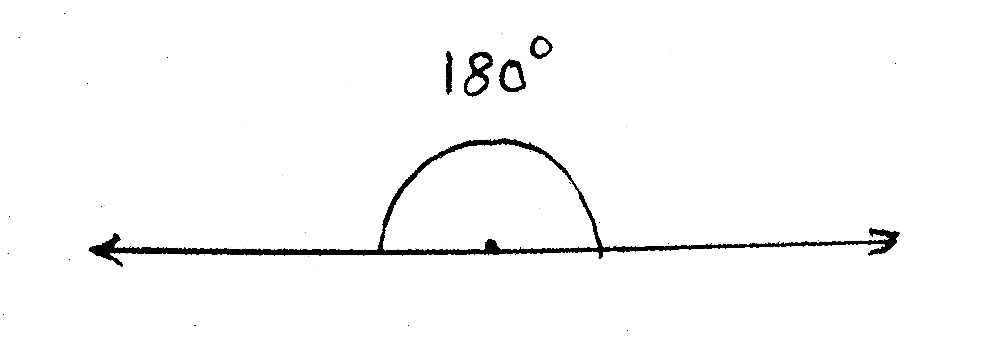
These are measured in two forms: Decimal form, and DMS form. In decimal form, angles are measured in degrees in decimal units. In DMS form, the decimal part of the degree is converted to Minutes (denoted by the symbol $'$) and Seconds (denoted by the symbol $^"$) using the conversion $60$ seconds = $1$ minute and $60$ minutes = $1$ hour.
Convert $45.325^{0}$ into DMS form.
Solution:
The integer part $45$ represents the degree part of the angle. We need to convert the decimal portion $0.325$ into minutes, using the fact that $60$ minutes make $1$ hour: $0.325^{0} = 0.325 \times 60' = 19.5'$. This gives the minutes portion of the angle as $19'$. Now, the decimal part of the minutes needs to be converted into seconds using the fact that $60$ seconds equals $1$ minutes: $0.5' = 0.5 \times 60^{"} = 30^{"}$. So, the angle in DMS form would be $45^{0} 19' 30^{"}$.
Convert $36^0 24' 12^"$ into decimal form.
Solution:
For this problem, we start with the seconds part. Convert the seconds part into minutes part by dividing it by $60$: $\frac{12}{60} = 0.2'$. Adding this decimal part to the minutes part, we get the minutes part as $24.2'$. Dividing this by $60$ would convert this into the decimal part of the degree: $\frac{24.2}{60} = 0.403^0$. So, the decimal form of this angle is $36.403^0$.
A radian is defined as the measure of the angle subtended by an arc of a circle at the center, where the length of the arc equals the radius of the circle.
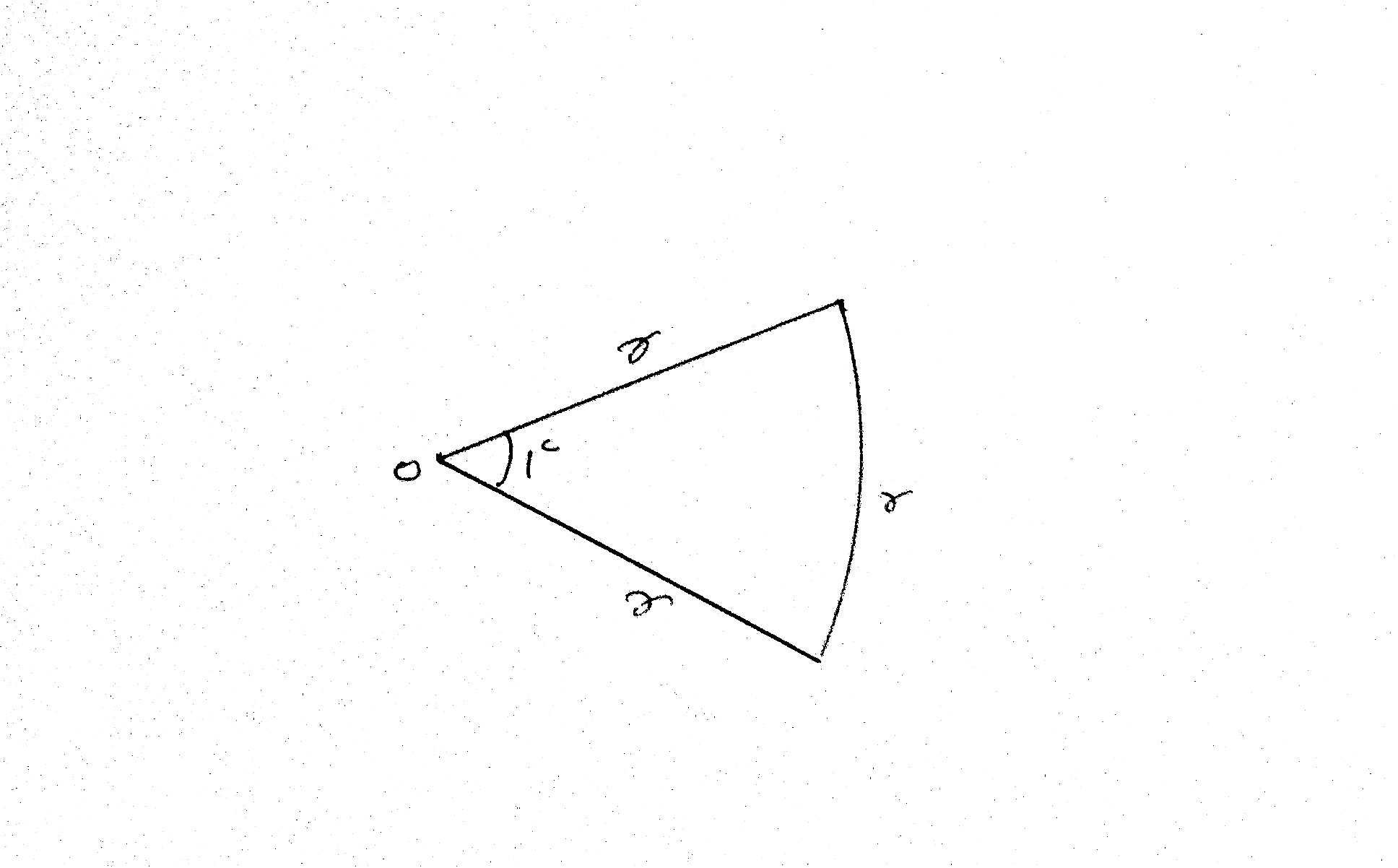
we know that the circumference of a circle with radius $r$ is $2 \pi r$. This means that, in any circle, there are $2 \pi$ arcs of length $r$. But we know that the measure of angle in degrees of a full circle at the center is $360^0$. Hence we have $2 \pi = 360^0$. that is, $\pi^c$ = $180^0$. This gives us a relationship between degrees and radians. To convert measures of angles from radians to degrees or degrees to radians, we use the proportion $\frac{a^0}{180^0} = \frac{b^c}{\pi^c}$. A radian measure is written either in terms of $\pi$ or as a decimal.
Convert $\frac{2\pi}{5}$ into degrees.
Solution:
Here we substitute the given radians into the proportion and solve: \begin{eqnarray} \frac{a^0}{180} &=& \frac{\frac{2\pi}{5}}{\pi}\\ a^0 &=& \frac{2\pi}{5} \times \frac{180}{\pi}\\ a^0 &=& 72^0\\ \end{eqnarray}
Convert $2.15$ radians into degrees.
Solution:
Substituting in the proportion rule and solving: \begin{eqnarray} \frac{a^0}{180} &=& \frac{2.15}{\pi}\\ a^0 &=& 2.15 \times \frac{180}{\pi}\\ a^0 &\approx & 123.2\\ \end{eqnarray}.
Convert $75^0$ into radians.
Solution:
Using the proportion rule and solving: \begin{eqnarray} \frac{b^c}{\pi} &=& \frac{75}{180}\\ b^c &=& 75 \times \frac{\pi}{180}\\ b^c &=& \frac{5 \pi}{12}\\ \end{eqnarray}.
Length of an arc of a circle is a part of the circumference of the circle. So, the ratio of the central angle $\theta$ of the arc to the central angle of the full circle is the same as the ratio of the length of the arc $l$ to the circumference of the circle. If the central angle $\theta$ is given in degrees, Then, this proportion becomes $\frac{\theta}{360} = \frac{l}{2\pi r}$, where $r$ is the radius of the circle. If the central angle $\theta$ is in radians, then the proportion becomes $\frac{\theta}{2\pi} = \frac{l}{2 \pi r}$. Simplifying, we get the formula $l = r \theta$. Remember that we can use this formula only if the central anglear is in radians. Central angle of an arc is also sometimes called measure of the arc.
Find the length of the arc of a circle of radius $4$ inches, if the arc subtends and angle of $50^0$ at the origin of the circle.
Solution:
Here, $r = 4$ and $\theta = 50^0$. So, we compute the length of the arc $l$ as: \begin{eqnarray} \frac{50}{360} &=& \frac{l}{2 \pi \times 4}\\ \frac{5}{36} &=& \frac {l}{8 \pi}\\ l &=& \frac{5 \times 8 \pi}{36}\\ l &=& \frac{10\pi}{9}\\ \end{eqnarray} So, length of the arc is exactly $\frac{10\pi}{9}$ inches. As $\pi$ is an irrational number, we can use calculator to find the length as $3.49$ inches approximately.
Find the length of the arc of a circle whose radius is $2.5$ cm given that the measure of the arc is $1.265^c$.
Solution:
As the central angle is given in radians, we use the formula $s = r\theta$: \begin{eqnarray} s &=& (2.5)(1.265)\\ &=& 3.1625\\ \end{eqnarray}
So,the length of the arc is $3.1625$ cm.
Determine the measure of the arc, in radians, of a circle of radius $6$ inches, given that the length of the arc is $3.8$ inches.
Solution:
Using the formula for radians, we get: \begin{eqnarray} 3.8 &=& 6 \times \theta\\ \theta &=& \frac{3.8}{6}\\ &\approx& 0.633\\ \end{eqnarray}
So, the measure of the arc is approximately $0.633$ radians
Determine the radius of a circle that has an arc of measure $45^0$ and length $3\pi$ inches.
Solution:
Using the formula for degrees, we have: \begin{eqnarray} 3\pi &=& \frac{45}{360} \times 2\pi r\\ &=& \frac{ \pi r}{4}\\ r &=& \frac{3 \pi \times 4}{\pi}\\ r &=& 12\\ \end{eqnarray}
So, the radius of the circle is $12$ inches.
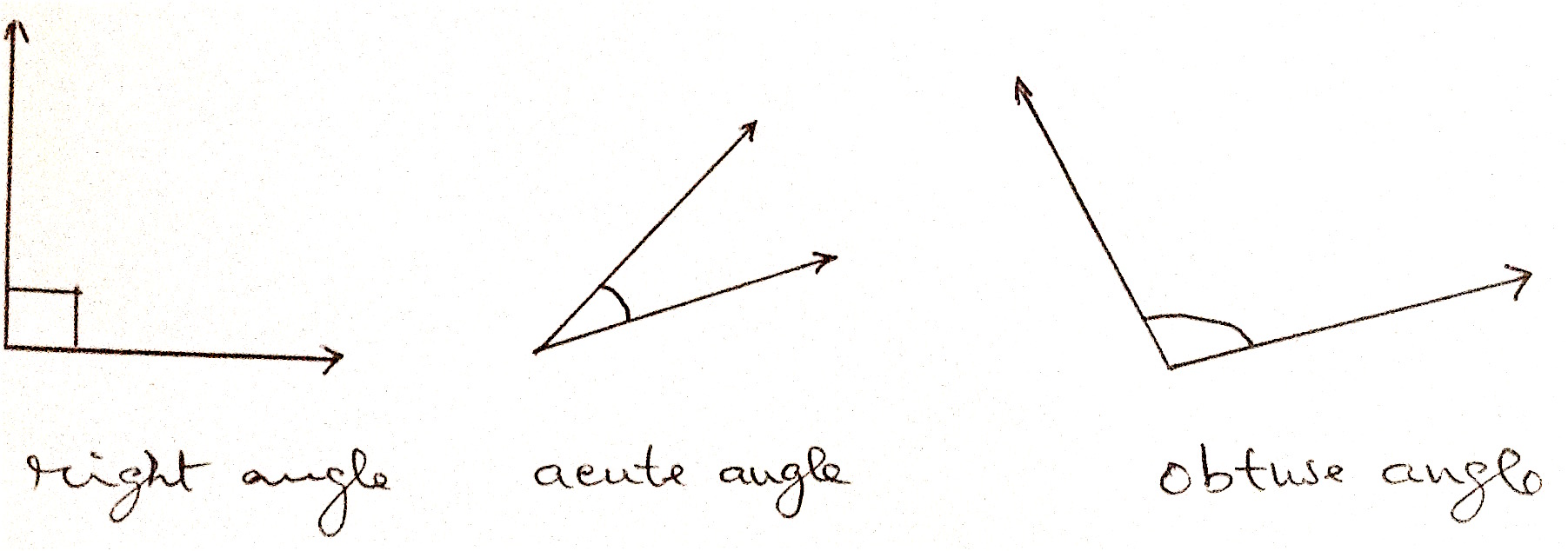
when an angle measures $90^0$, it is called a right angle. An angle that measures less than $90^0$ is called acute angle. an angle that measures more than $90^0$ is called obtuse.
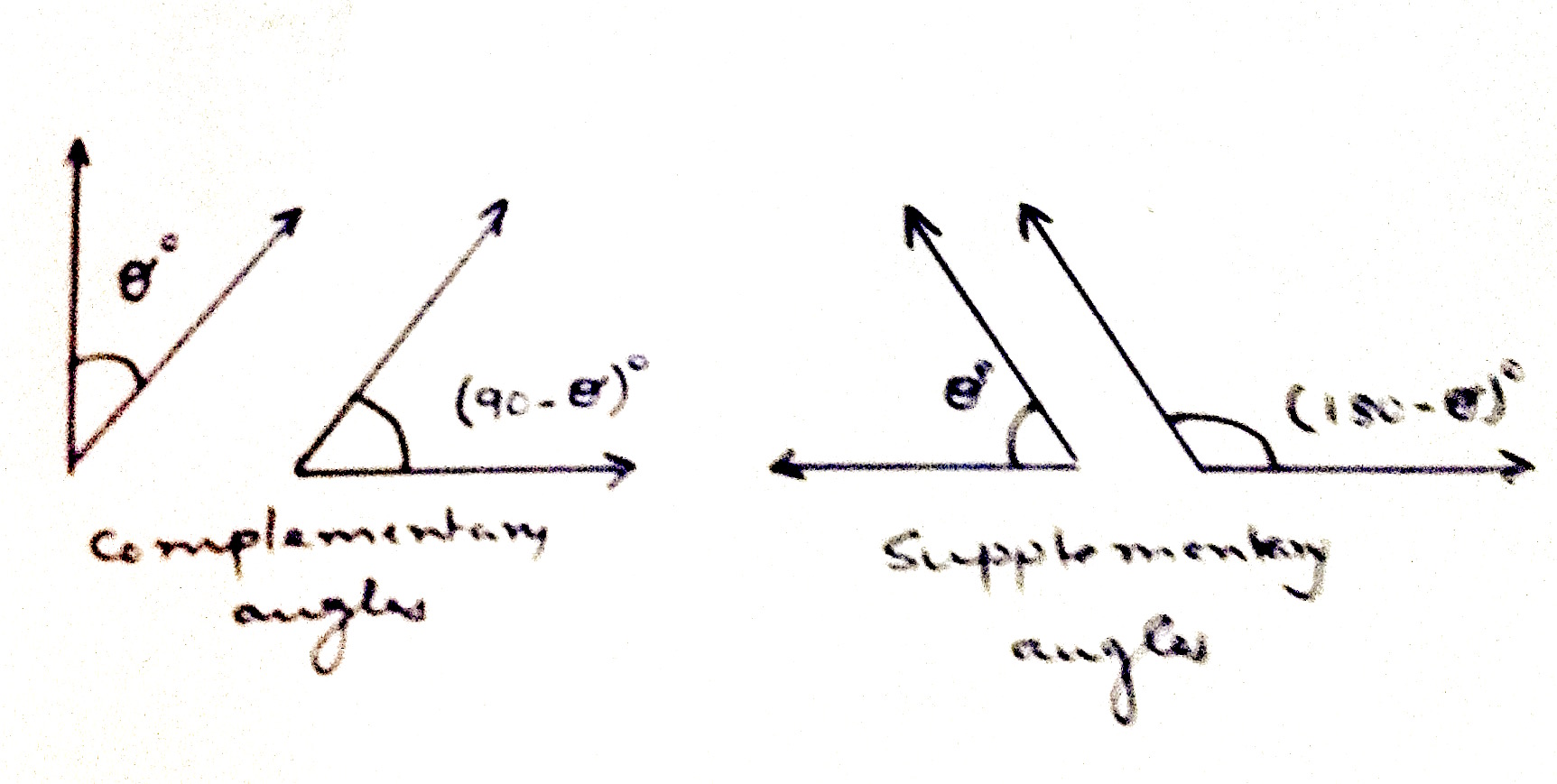
Two angles are said to be complementary angles if their measures adds up to $90^0$ or $\frac{\\pi}{2}$n radians, and supplementary angles if their measures adds up to $180$ or $\pi$ radians. Two angles that are adjacent and supplementary are called angles in a linear pair.
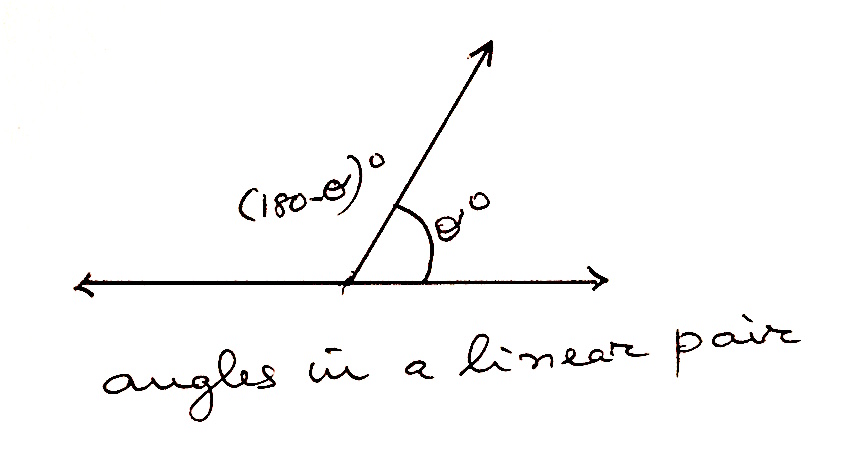
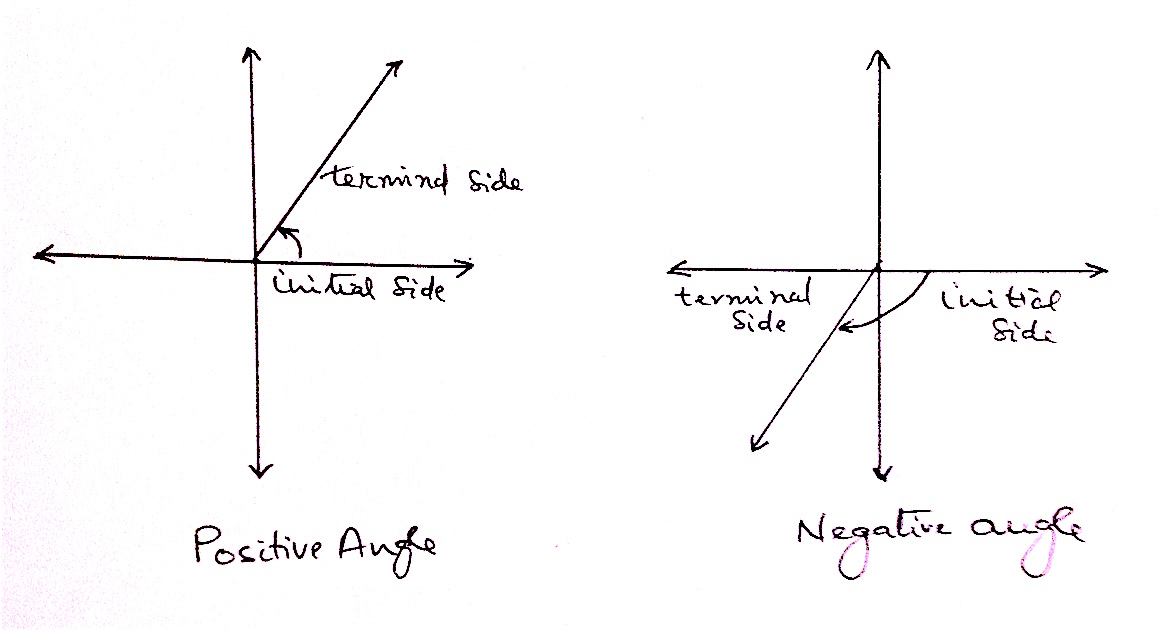
Any angle whose vertex coincides with the origin of a rectangular coordinate system and on ray coincides with the positive side of the $x$- axis is called angle in standard position . In this position, the ray the coincides with the positive side of $x$- axis is called the initial side and the other ray is called the terminal side. Any angle can be copied and embedded in a rectangular coordinate system such that the vertex coincides with the origin and one ray coincides with the posive direction of $x$- axis. This standard position af an angle helps to analyze and derive many ideas and interpretations. In this standard position, an angle is always measured from the initial side to the terminal side.
Angle angle has positive measure if it is measure from the initial in the counter-clockwise direction (anti-clockwise direction). If an angle is measured from the initial side in the clockwise direction,it is said to be a negative angle.
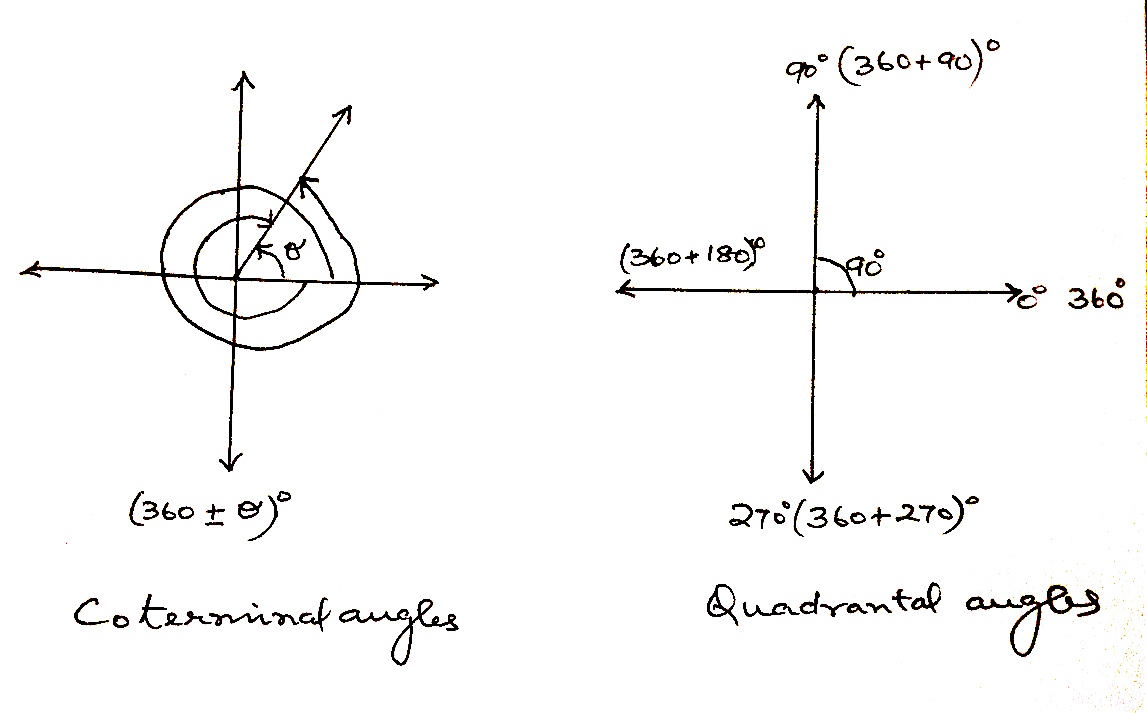
Based on the idea of angle in standard position, was following definitions can be deduced:
Identify whether the following angles are acute, obtuse, or reflex:
$(a) \quad 95^0$ $(b) \quad 207^0$ $(c) \quad \frac{3\pi}{5}^c$ $(d) \quad \frac{13\pi}{9}$
Solution:
$(a)$ Obtuse $(b)$ Reflexive $(c)$ Obtuse $(d)$ Reflexive
Find the complementary angles to the following angles:
$(a) \quad 28.6^0$ $(b) \quad \frac{7\pi}{15}$ $(c) \quad 18^0 20' 36^{"}$ $(d) \quad 1.28^c$
Solution:
$(a) \quad 61.4^0$ $(b) \quad \frac{\pi}{30}^c$ $(c) \quad 71.66^0$ $(d) \quad 0.29^c$
Find the supplementary angles for the following:
$(a) \quad 127.42^0$ $(b) \quad 131^0 12' 40^{"}$ $(c) \quad 2.18^c$ $(d) \quad \frac{5\pi}{9}$
Solution:
$(a) \quad 52.58^0$ $(b) \quad 48.79^0$ $(c) \quad 0.342^c$ $(d) \quad \frac{4\pi}{9}$
Find one positive and one negative co-terminal angles for the following:
$(a) \quad 75^0$ $(b) \quad \frac{\pi}{5}$
Solution:
$(a) \quad 435^0, -315^0$ $(b) \quad \frac{11\pi}{5}, \frac{9\pi}{5}$
Graph the following angles in standard position, show the orientation of the terminal side, and determine the quadrant in which the angle lies.
$(a) \quad 330^0$ $(b) \quad -220^0$ $(c) \quad \frac{7\pi}{2}^c$ $(d) \quad -\frac{5\pi}{6}^c$
Solution:
$(a)$ 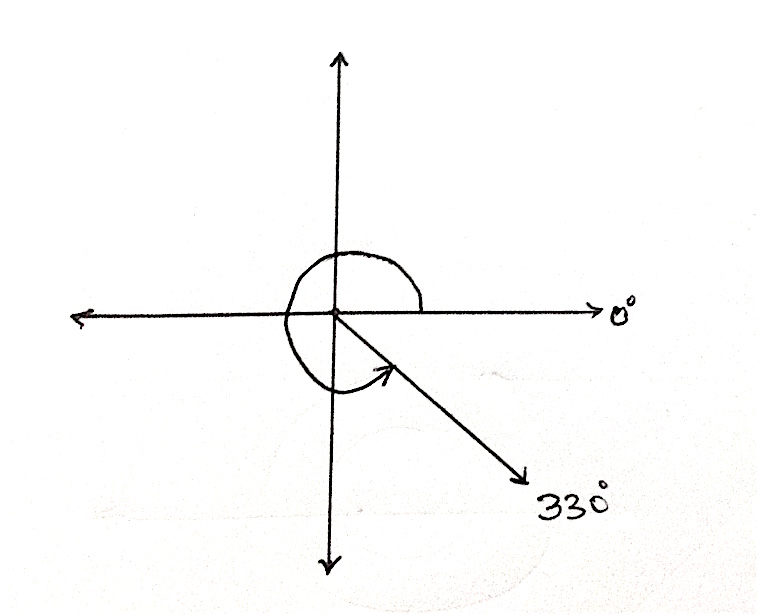 4th quadrant.
4th quadrant.
$(b)$ 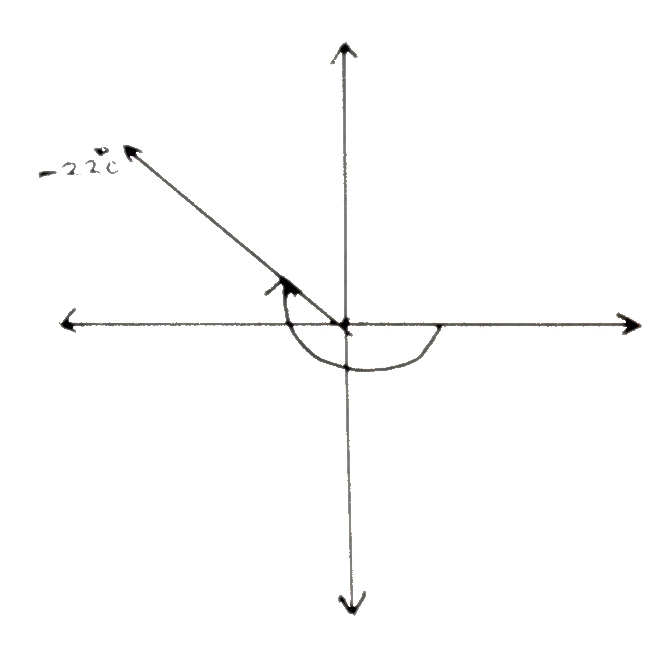 2nd quadrant.
2nd quadrant.
$(c)$ 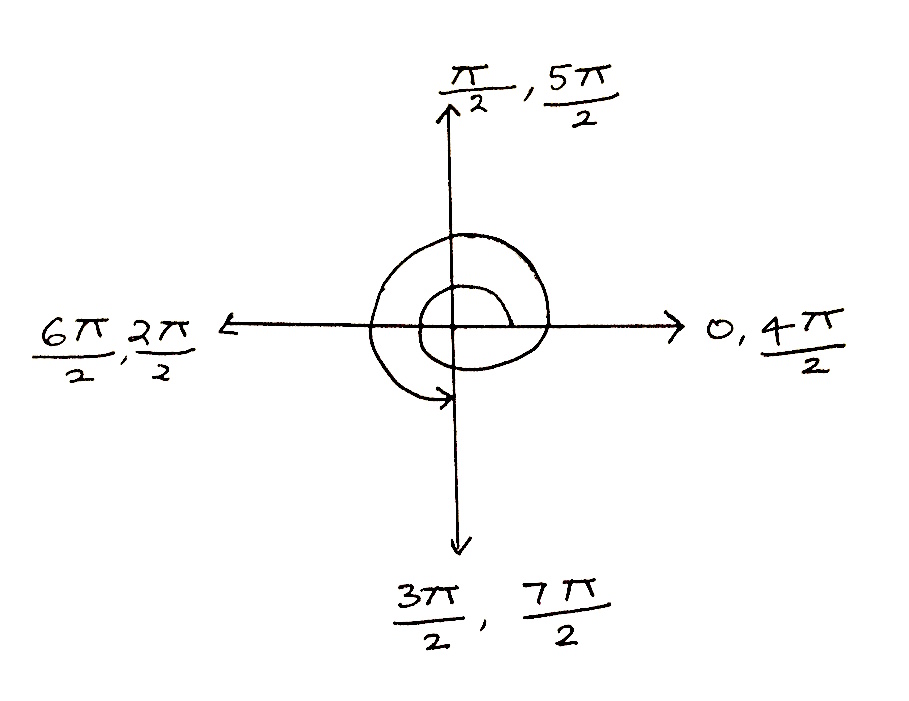 Quadrantal angle.
Quadrantal angle.
$(d)$ 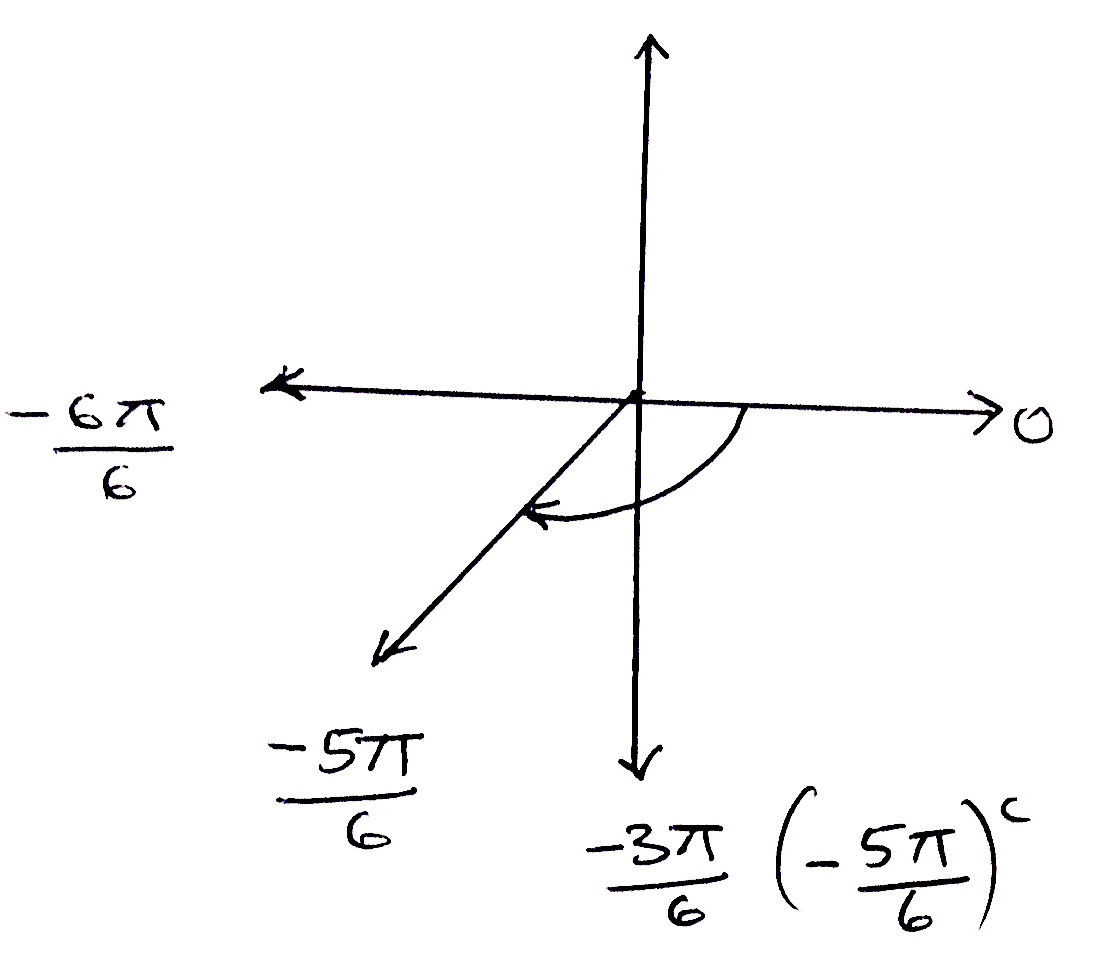 3rd quadrant.
3rd quadrant.
When a particle moves in a circular path, it experiences both linear speed as well as angular speed. Linear speed is the length of the arc of the circle covered by the particle per unit time, and the angular speed is the measure of the arc of the circle, in radians, covered by the particle per unit time. By this definition, linear speed $v$ is computed using the formula $v = \frac{l}{t}$ and angular speed $w$ is computed using the formula $w = \frac{\theta}{t}$. Linear speed and angular speed are related using the formula $l = \theta r$ as below: \begin{eqnarray} v &=& \frac{l}{t}\\ &=& \frac{r \theta}{t}\\ r \times \frac{\theta}{t}\\ &=& rw\\ \end{eqnarray}
Find the linear speed of a particle moving on a circular path of radius 4 inches, if it covers an angle of $\frac{2\pi}{3}$ ra degdians per minute.
Solution:
Here, $w = \frac{2\pi}{3}$ and $r = 4$. So, we have $v = \frac{2\pi}{3} \times 4$. So, linear speed is $\frac{8\pi}{3}$ inches per minute.
A wheel of diameter $24$ inches rotates $75$ times per minute. Find the linear speed in feet per minute and angular speed of the wheel in radians per minute.
Solution:
The wheel covers an angle of $2 \pi$ radians in one rotation, and also covers a distance of $2 \pi r$ inches in one rotation. So, in $75$ rotations, the wheel covers $75 \times 2\pi$ radians and $75 \times 2 \pi r$ inches. This gives the linear and angular speeds as below: \begin{eqnarray} w &=& 75 \times 2\pi\\ &=& 150 \times \pi \\ &\approx& 471.24\\ v &=& 75 \times 2\pi(2)\\ &=& 300\pi\\ &\approx& 942.47\\ \end{eqnarray}
So, angular speed of the wheel is approximately $471.24$ radians per minutes and the linear speed is approximately $942.47$ feet per minute.
One revolution of a wheel of any circular path equals $2\pi$ radians, and the distance traveled in one revolution is $2\pi r$. In this sense, we note that 1 radius = 1 radian. So, we can use a series of unit conversion factors to compute linear or angular speeds when revolution is given.
A wheel of radius $15$ inches is rotating at 520 rotations per minute. Find the wheel's linear speed in miles per hour.
Solution:
Here, we compute the linear speed in miles per hour as shown below: \begin{eqnarray} \frac{520 rev}{1 min} \times \frac{2\pi^c}{1 rev} \times \frac{15^{"}}{1^c} \times \frac{1'}{12^{"}} \times \frac{1 mile}{5280'} \times \frac{60 min}{1 hr}\\ &-& \frac{520 \times 2\pi \times 15 \times 60}{12 \times 5280} \frac{miles}{hour}\\ &\approx& 46.61 miles/hour\\ \end{eqnarray}
The region bounded an arc and the two radii at the end points of the arc is called a sector. Perimeter of a sector equals the sum of the length of the arc and the two radii at the end points: $P = s + 2r$.
Are of the sector is the portion of the area of the whole circle cut by the central angle. that is $A = \frac{\theta^0}{360^0} \pi r^2$square units if $\theta$is in degrees, or $A = \frac{\theta^c}{2\pi} \pi r^2$square units if $\theta$ is in radians. Using the formula $s = r \theta $, we can simplify this formula as $A = \frac{1}{2}sr$
The region bounded by an arc and the chord joining the end points of that arc is called a segment. Perimeter of the segment is the sum of the length of the arc and the length of the chord. Area of the segment is computed by subtracting the area of the triangle formed by the chord and the two radii from the area of the sector.
An arc$(AOB)$ of a circle of radius $5$cm makes a central angle of $\frac2\pi}{3}$radians.. Find:
$(a)$ the perimeter of the sector formed by the arc;
$(b)$ The area of the sector formed by the arc;
$(c)$the area of the segment formed by the arc and the chord joining the end points of the arc.
Solution:
$(a)$ $s=r\theta \implies s = \frac{5\pi}{3}$ cm. Perimeter of the sector $P = \left(\frac{5\pi}{3} + 10\right)$cm.
$(b)$ Area of the sector $A = \frac{1}{2} (sr) \implies A = \frac{25 \pi}{6}$ sq.cms.
$(c)$ Area of the segment = Area of the sector - Area of the triangle.
As the central angle is $\frac{\pi}{3}$, the triangle formed by the radii and the chord is an equilateral triangle.
Hence we have $A = \left(\frac{25\pi}{6} - \frac{25\sqrt{3}}{4} \right)$ sq.cms.
$25.2^0$
$18.38^0$
$38^0 12^{'}$
$104^0 43' 12^{"}$
$0.92^c$
$\frac{3\pi}{4}$
$302.52^0$
$100^0$
$50$ inches
$50.13$ cm.
$2.29$ inches
$4.17$ radians
$2.25$ radians
$(a)$ Acute $(b)$ Obtuse.
$(a$ Complementary $(b)$ Supplementary $(c)$ co-terminal
$(a) \quad -317^0 3' 30^{"}$ $(b) \quad 114^0 32' 1^{"}$ $(c) \quad 179^0 59' 56^{"}$
$(a) \quad \frac{4\pi}{3}$ $(b) \quad - \frac{5\pi}{6}$ $(c) \quad \frac{5\pi}{4}$
$(a) \quad 300^0$ $(b) \quad -72^0$ $(c) \quad 675^0$
$(a)$  $(b)$
$(b)$ 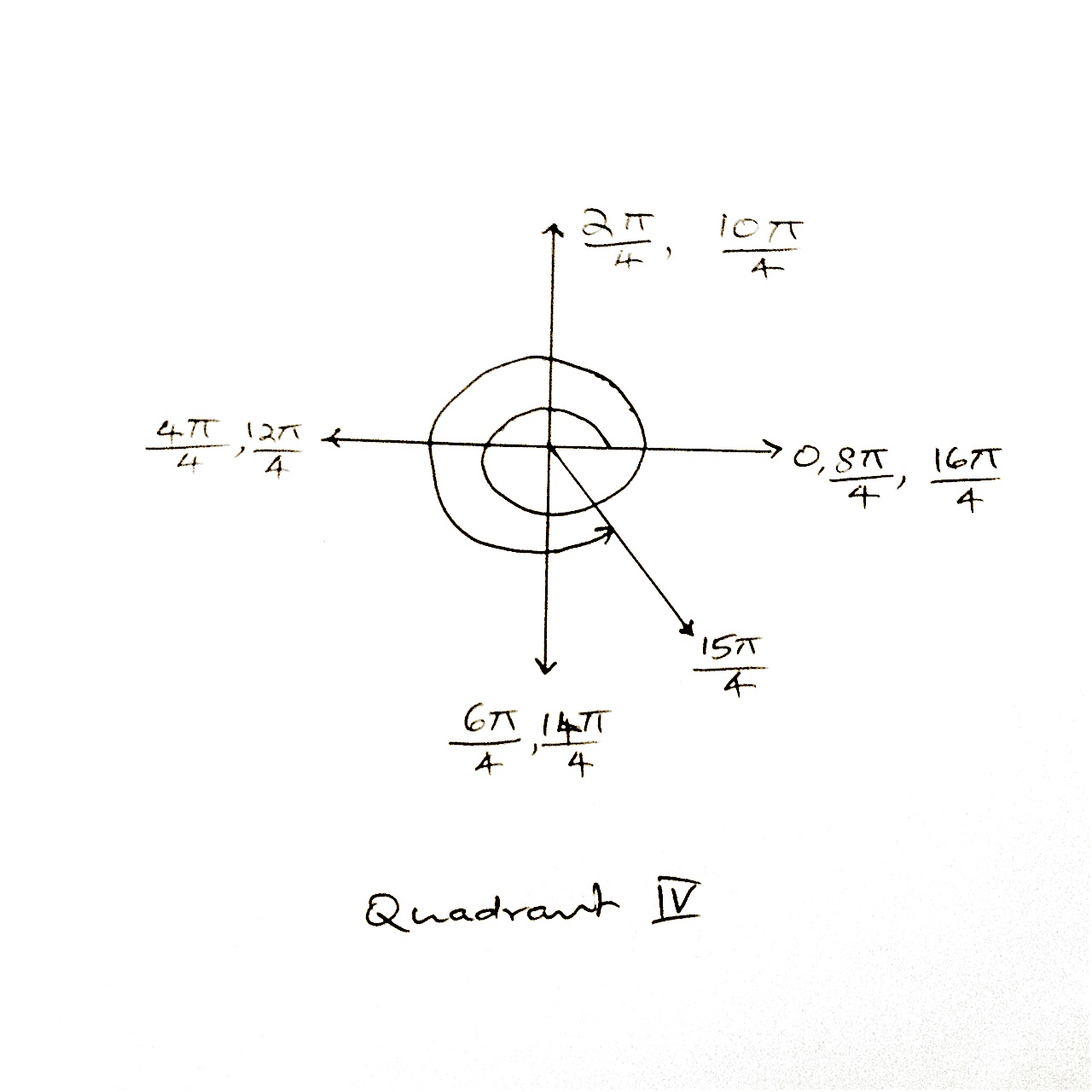 $(c)$
$(c)$ 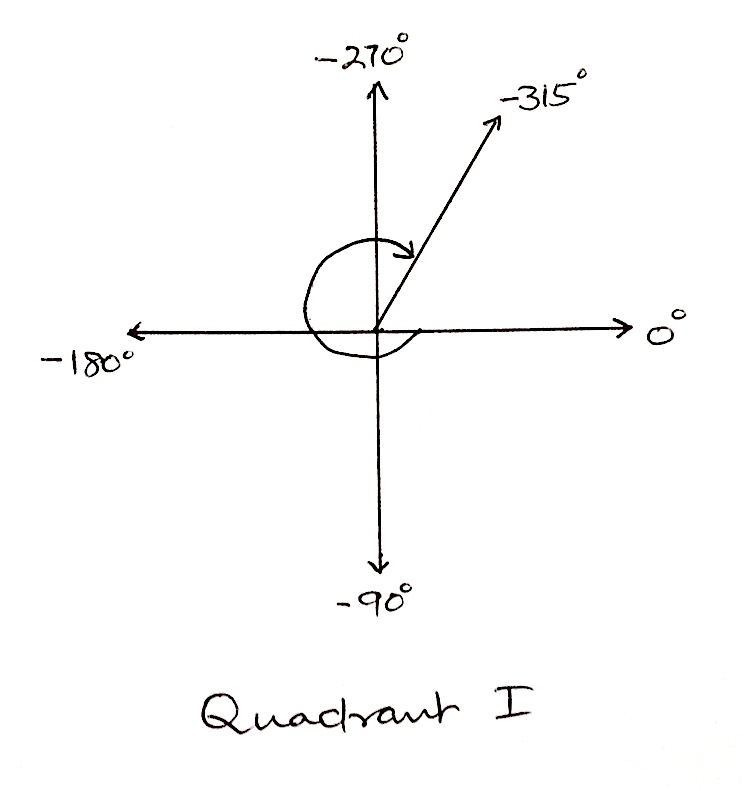 $(d)$
$(d)$ 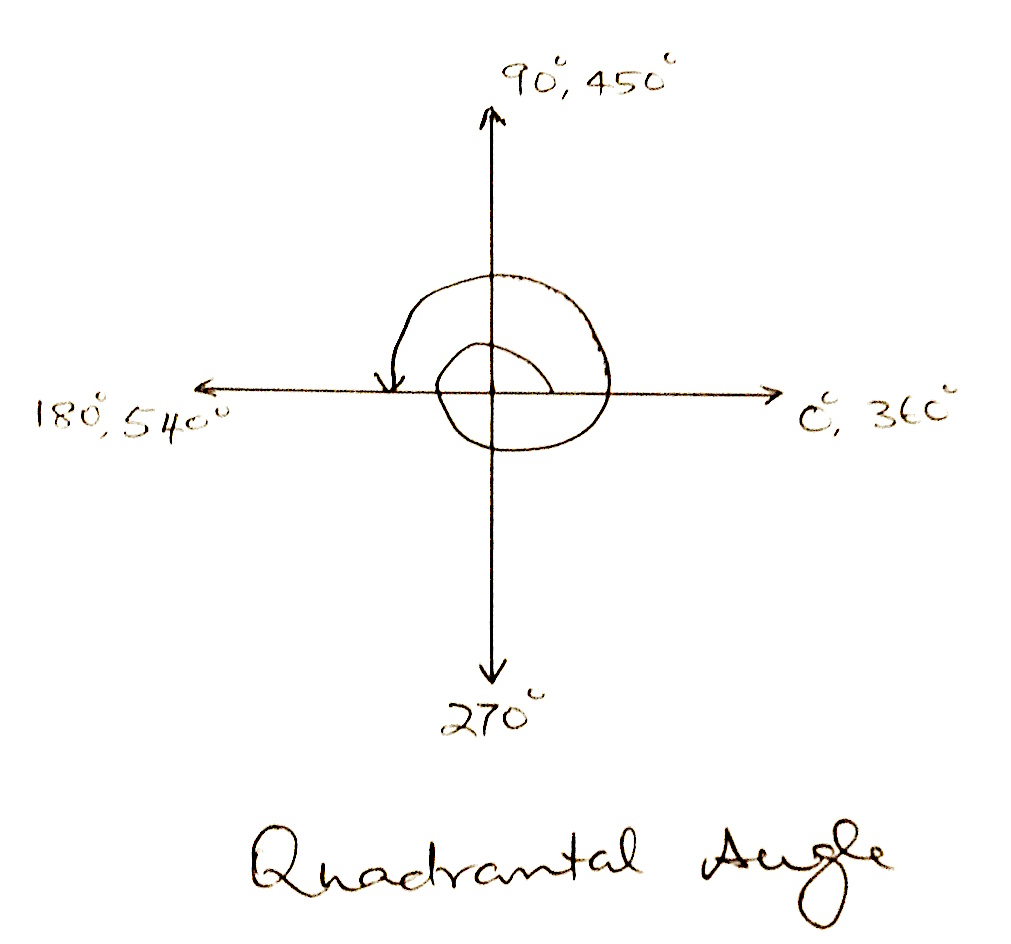
Linear speed is about $30.2$ miles per hour. Angular speed is $187.5\pi$ radians per second.
$s_1=(r_1)(\theta)$. So, $\theta = \frac{9}{11}$radians; $s_2=(r_2)(\theta)$. So, $s_2 = 36$cm.
Linear speed is $35$ feet per second.
Angular speed is approimately $6.08$ radians per minute.
Approximately $30.12$ miles per hour.
$70$ miles per hour
About 4.32 miles per hour.