Dr. Lalitha Subramanian
About the Author

Aksharam
One of the many applications of exponential functions is growth and decay situations. For any exponential function $f(x)=a(b)^x$ we note that $f(x+1)= a(b)^{x+1} = a(b)^x \times (b)^1 = b\times a(b)^x = bf(x)$. Hence, as $x$ increases, the value of $y$ becomes a multiple of the same function. Hence this function is an exponential growth function when $a \gt 0$ and $b \gt 1$, and an exponential decay function when $a \gt 0$ and $b \lt 1$.The base $b$ is called the growth/decay factor.
Population of a city was $465,622$ in the year $1900$ and it increased to $656,562$ in $2000$. Based on this data, when did the population surpass $800,000$?
Solution:
Setting the year $1900$ as $t = 0$, we have the function $P(t) = P_{0}(b)^t$ to represent the growth of the population of the city, where $b$ represents the growth factor. Setting $t = 0$, we have $P(0)=4656,22$. Substituting these values in the equation: \begin{eqnarray} P(t) &=& P_{0}(b)^t\\ 465,622 &=& P_{0}(b)^0\\ 465,622 &=& P_{0}\\ \end{eqnarray} Now, rewriting the function with the initial value, we have $P(t)=465,622(b)^t$. The data states that the population increased to $4656562$ in $2000$. With $t = 0$ representing the year $1900$, we have the year $2000$ as $t = 10$. So, substituting the values of $P(10)$ and $t$ in this equation, we find the growth factor. \begin{eqnarray} P(10) &=& 465,622(b)^{10}\\ 656,562 &=& 465,622(b)^{10}\\ b^{10} &=& \frac{656,562}{465,622}\\ b^{10} &=& 1.41008\\ 10 &=& \log_{b}{1.41008}\\ 10 &=& \frac{\ln{1.41008}}{\ln{b}}\\ \ln{b} &=& \frac{1.41008}{10}\\ \ln{b} &=& 0.034365\\ b &=& e^{0.034365}\\ b & \approx & 1.035\\ \end{eqnarray} Now, we have the revised function as $P(t) = 465,622(1.035)^t$. To find the year in which the population became $800,000$, we substitute this value in the above equation and determine the value of $t$: \begin{eqnarray} 800,000 &=& 465,622(1.035)^t\\ \frac{800,000}{465,622} &=& (1.035)^t\\ (1.035^t &=& 1.718132\\ t &=& \log_{1.035}{1.718132}\\ t &=& \frac{\ln{1.718132}}{\ln{1.035}}\\ t &\approx& 15.7\\ \end{eqnarray} This means that the population surpassed $800,000$ in the 16th year after $1900$, which is $2016$.
The amount $C$ in grams of carbon present in a substance after $t$ years is given by $C = 20e^{-0.0001216t}$.
$(a)$ What was the initial amount of carbon present in the substance?
$(b)$ How much was left after $10,400$ years?
$(c)$ When will the amount be $10$ grams?
Solution:
$(a)$ To find the initial amount, set $t=0$ and solve for $C$: \begin{eqnarray} C &=& 20e^{-0}\\ &=& 20\\ \end{eqnarray} So, there was 20 grams of carbon present in the substance initially.
$(b)$ Substitute $t=10,400$ and solve for C: \begin{eqnarray} C &=& 20e^{-0.0001216\times10,400}\\C &=& 20e^{-1.26464}\\ C & \approx & 0.2823\\ \end{eqnarray} So, after $10,400$ years, approximately $0.28$ grams of carbon was present in the substance.
$(c)$ Substituting $ C=10$ and solving for $t$: \begin{eqnarray} 10 &=& 20e^{-0.0001216t}\\ 0.5 &=& e^{-0.0001216t}\\ -0.0001216t &=& \ln{0.5}\\ t &=& \frac{\ln{0.5}}{-0.0001216}\\ t &\approx& 5700\\ \end{eqnarray} After $5700$ years, 10 grams of carbon will be present in the substance.
Some real life situations like radio-active decay are modeled by exponential function of base different from $e$. In particular, problems involving half-life of substances can be easily done using exponential function, with base $\frac{1}{2}$. Following two examples illustrate this.
The half-life of a radio-active substance is $65$ days. There are $6.6$ grams present initially.
$(a)$ Express the amount of the substance remaining as a function of time $t$.
$(b)$ When will there be less than $1$ gram remaining?
Solution:
$(a)$ Given that the substance becomes half in $65$ days, This means that, if $t$ amount of substance remaining after $t$ days is modeled by the function $$ m(t)=m_{0}\left(\frac{1}{2}\right)^{\frac{t}{65}},$$ where $m_{0}$ is the initial mass of the substance. Substituting the initial value, we have $$ m(t) = 6.6\left(\frac{1}{2}\right)^{\frac{t}{65}}$$.
$(b)$ Substituting $m(t) = 1$ and solving for $t$: \begin{eqnarray} m(t) &=& 6.6\left(\frac{1}{2}\right)^{\frac{t}{65}}\\ 1 &=& 6.6\left(\frac{1}{2}\right)^{\frac{t}{65}}\\ \left(\frac{1}{2}\right)^{\frac{t}{65}} &=& \frac{1}{6.6}\\ &=& 0.15152\\ \frac{t}{64} &=& \log_{\frac{1}{2}}{0.15152}\\ t &=& 64\left(\frac{\ln{(0.15152)}}{\ln{(0.5)}}\right)\\ t &\approx& 177\\ \end{eqnarray} So, the amount of the substance becomes $1$ gram in $177$ days.
The population of a certain city was $28,500$ in the year $1980$. The population was doubling every $12$ years.
$(a)$ Express the population of that city $t$ years after $1980$ as a function of $t$.
$(b)$ Estimate the population of the city in the year $2000$.
$(c)$ When will the population surpass $1,500,000$?
$$P(t) = 28,500(2)^{\frac{t}{12}}$$
$(b)$ The initial population is given to be in the year $1980$ So, taking $t = 0$ for this year, we have $t=20$ for the year $2000$. Substituting this value of t in the function and solving for P(20): \begin{eqnarray} P(t) &=& 28,500(2)^{\frac{20}{12}}\\ &=& 28,500(2)^{1.66667}\\ &\approx& 90481.86\\ \end{eqnarray} As population cannot be in decimal, we conclude that the population of the city would be approximately $90481$ in the year $2000$.
$(c)$ Substituting $P=1,500,000$ and solving for $t$: \begin{eqnarray} 1,500,000 &=& 28,500(2)^{\frac{t}{12}}\\ \frac{1,500,000}{28,500} &=& 2^{\frac{t}{12}}\\ 52.63156 &=& 2^{\frac{t}{12}}\\ \frac{t}{12} &=& \frac{\ln{(52.63156)}}{\ln{(2)}}\\ t &=& 12\left(\frac{\ln{(52.63156)}}{\ln{(2)}}\right)\\ t &\approx& 68.61\\ \end{eqnarray} As $t=0$ refers to the year $1980$, we conclude that the population would surpass $1,500,000$ in the year $2050$.
If the population $P$ is changing at a constant percentage rate $r$ each year, we can use the compound interest formula to model the population of any given year: $$ P(t) = P_{0}(1+r)^t$$ Here, $P_{0}$ is the initial population , the percent rate $r$ is expressed as a decimal, and $t$ is the time in years. While doing these problems, Note the following:
The initial population of a certain type of bacteria is $250$. The population of this bacteria is increasing at a rate of $4.6%$ every day.
$(a)$ Express the population of the bacteria at any time as a function of $t$.
$(b)$ What will be the population of the bacteria 6 days after the initial counting?
$(c)$ when will the population become $1000$?
Solution:
$(a)$ Initial population $P_{0}=250$, and the rate of increase per day is $4.6% = 0.046$ expressed as decimal. So, the model for this problem would be $$ P(t)=250(1+0.046)^t$$.
$(b)$ Substituting $t = 6$ in the model and solving for $P(t)$: \begin{eqnarray} P(t) &=& 250(1.046)^6\\ &\approx& 327\\ \end{eqnarray} Answer: $6$ days after the initial counting, the number of bacteria would be 327.
$(c)$ Substituting $P(t)=1000$ and solving for $t$: \begin{eqnarray} 1000 &=& 250(1.046)^t\\ \frac{1000}{2150} &=& (1.046)^t\\ 4 &=& (1.046)^t\\ t &=& \log_{1.046}{4}\\ &=& \frac{\ln{(4)}}{\ln{(1.046)}}\\ &\approx& 30.8\\ \end{eqnarray} Answer: The population of the bacteria would become $1000$ in $39$ days after the initial counting.
Whenever the growth/decay has restrictions on range, a logistic function is an appropriate model. The following example illustrates the process of solving problems involving logistic functions.
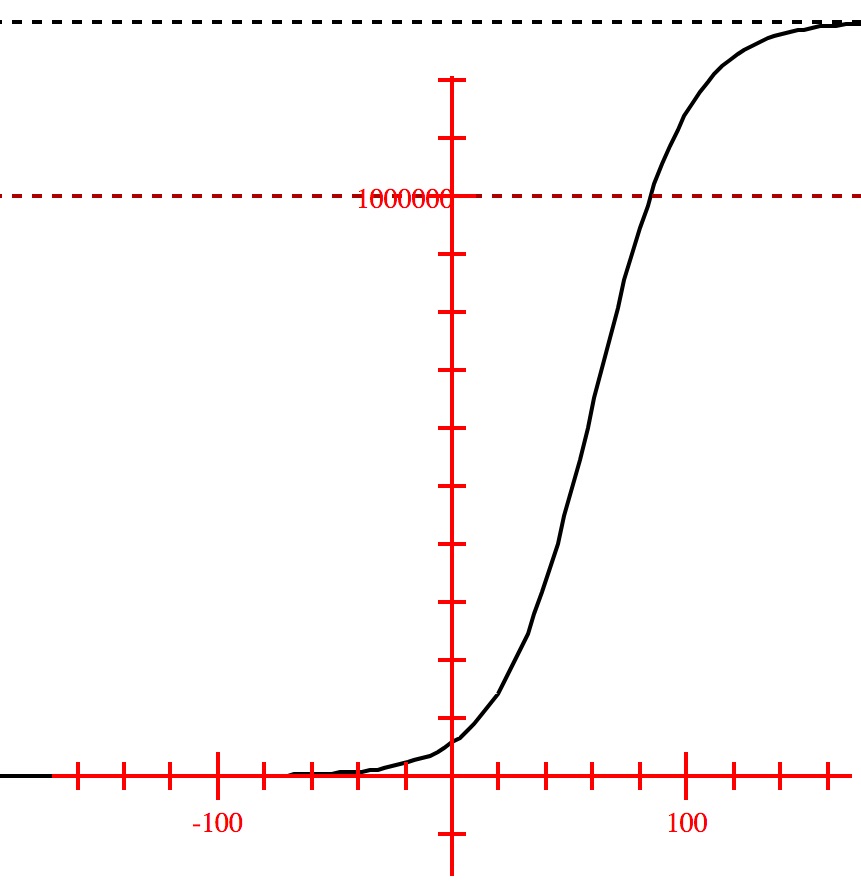
A logistic model of the population of a city, $t$ years after $1900$ is $$P(t) = \frac{1,301,642}{1+21.602e^{-0.05054t}}$$. According to this model, when did the population of the city cross $1,000.000$?
Solution:
Substituting $P(t) = 1,000.000$ and solving for t:
\begin{eqnarray} 1,000,000 &=& \frac{1,301,642}{1+21.602e^{-0.05054t}}\\ 1+21.602e^{-0.05054t} &=& \frac{1,301,642}{1,000,000}\\ &=& 1.301,642\\
21.602e^{-0.05054t} &=& 0.301642\\ e^{-0.05054t} &=& \frac{0.301642}{21.602}\\ &=& 0.0139636\\ -0.05054t &=& \ln{0.0139636}\\
t &=& \frac{\ln{0.139636}}{-0.05054}\\ t &\approx& 84.5\\ \end{eqnarray} As the initial value of $t = 0$ corresponds to the year $1900$, we conclude
that the population of the city surpassed $1,000,000$ 85 years after, that is, in the year $1985$. The restriction in the range of this model and the
intersection of the horizontal line $y = 1,000,000$ at the point approximately$x = 84.5$ can be seen clearly in the graph shown below:
Some of the various applications of logarithmic functions include models that determine and\or compare chemical acidity, intensity of Richter Scale magnitude of earthquake at a place, spread of rumor, spread of infections, modeling the level of sound intensity, etc. A few of these models are illustrated below.
The level of sound intensity in decibels , whose unit is denoted by dB is defined by the formula $$\beta = 10\log{\left(\frac{I}{I_{0}}\right)}$$ where $\beta$ is the number of decibels, $I$ is the sound intensity in watts per square meter, and $I_{0}$ is a constant the refers to human hearing threshold. In a quiet place, our audible sound intensity is $I_{0} = 10^{-12}$ watts per square meter. The intensity of sound $I$ may vary to the place and the circumstances. For example, in city traffic, $I_{0} = 10^{-5}$ $W/m^2$, at a place a jet is taking off, $I_{0}= 10^3$, etc.
How loud is the city traffic, based on the intensity of sound of city traffic?
Solution:
Based on the data given above, we have $I = 10^{-5}$. So, the level os sound intensity in a city traffic is: \begin{eqnarray} \beta &=& 10\log{\left(\frac{10^{-5}}{10^{-12}}\right)}\\ &=& 10\log{(10^7)}\\ &=& 10(7)\\ &=& 70\\ \end{eqnarray} So, the level of sound intensity in the midst of city traffic would be $70$ dB.
The number of students infected with flu at a school after $t$ days is modeled by the function $N(t)=\frac{800}{1+49e^{-0.5t}}$.
$(a)$ What was the initial number of students infected with flu ?
$(b)$ When will the number of infected students become $250$?
$(c)$ What is the maximum number of students that could possibly infected by the flue?
$(d)$ How many students would be infected after $15$ days?
Solution:
$(a)$ Substituting $t=0$ in the function, we get: \begin{eqnarray} N(0) &=& \frac{800}{1+49e^0}\\ &=& \frac{800}{50}\\ &=& 16\\ \end{eqnarray} So, Initially 16 students were infected.
$(b)$ Substituting $N=250$, we get \begin{eqnarray} 250 &=& \frac{800}{1+49e^{-0.2t}}\\ 1+49e^{-0.2t} &=& \frac{250}{800}\\ &=& 0.3125\\ 49e^{-0.2t} &=& -0.6875\\ e^{-0.2t} &=& -0.01403061224\\ -0.2t &=& \ln{0.01403061224}\\ &=& -4.26651372652\\ t &\approx& 21.3\\ \end{eqnarray} So, The number of infected students would become $250$ after $21$ days.
$(c)$ Maximum number of student that could be possibly infected is $800$.
$(d)$ Substituting $t = 15$ in the equation: \begin{eqnarray} N(15) &=& \frac{800}{1+49e^{(-0.2)(15)}}\\ &=& \frac{800}{1+49e^{-3}}\\ &\approx& 233\\ \end{eqnarray} So, the number of infected students after $15$ days would be approximately 233.
Newton's Law of Cooling models the rate at which an object that has been heated will cool to the temperature of the medium in which it is placed. The model is given by $T(t) = T_{m} + (T_{0} - T_{m})e^{-kt}$, where $T_{m}$ is the temperature of the medium and $T_{0}$ is the initial temperature of the object.
An object at a temperature of $90^{\circ}C$ is placed in a medium whose temperature is $15^{\circ}C$. Three minutes later, the temperature of the object is $60^{\circ}C$. Use Newton's Law to find the time when the object will reach the temperature of $25^{\circ}C$.
Solution:
In chemistry, the acidity of any water-based solution is measured, written as $pH$, by the concentration os hydrogen ions in the solution, in moles per liter, written as $[H^+]$, by the relationship $pH=-\log[H^+]$. More acidic solutions have higher hydrogen concentration levels and less pH values.
What is the acidity level of a solution in which hydrogen ion concentration is $3.98 \times 10^{-3}$?
Solution:
Substituting the value of $[H^+]$ in the function, we get: \begin{eqnarray} ph &=& -\log{3.98\times 10^{-3}}\\ &\approx& 2.4\\ \end{eqnarray} So, the acidity of this solution is $2.4$
Another major application of exponential and logarithmic functions is in the field of finance. Following formulas model few of the applications:
$(a)$ There were $100$ bacteria present initially; $(b)$ After $6$ hours, there are $3694$ bacteria present.
$(a)$ The required model is $y = 16(1.08)^x$, where $y$ is the value after $x$ months; $(b)$ After $2$ years, the value of the item is approximately $21.77$
$(a)$ The model for this situation is $P = 65,300(0.982)^x$, where $P$ is the population of the city after $x$ years; $(b)$ After $5$ years, the population of the city is $59630$;
$(a)$ Model: $y = 250(2)^{\frac{t}{5}}$; $(b)$ After $20$, there will be $4000$ bacteria.
$(a)$ Model: $m = 200(0.5)^{\frac{t}{30}}$ after $40$ hours, mass of the substance is approximately $66$ grams; $(c)$ Mass of the substance will be at most $2$ grams after 200 hours.
$(a)$ $m = 50(0.5)^{\frac{t}{32}}$; $(b)$ Four days after the initial count, the mass of the substance is $6.25$ grams; $(c)$ The substance becomes less than $1$ gram after 181 days, that is, after approximately $7.5$ days.
Approximately $37.6$ miles above sea-level.
$(a)$ Substituting $t=0$, the initial population is $11$; $(b)$ Population of deer will be $600$ after approximately 24.5 years; $(c)$ Maximum possible deer in the park is $1001$.
$(a)$ The maximum number of people the rumor can spread is $789$. $(b)$ Initially, the rumor started with 46 people. $(c)$ The spread of the rumor will excees $600$ after $49$ hours.
$R=6.347$
$(a)$ Stomach acid: $[H^+] = 10^{-2}$ moles per liter; Blood: $[H^+]=3.98 \times 10^{-8}$; $(b)$ The hydrogen ion concentration of the stomach is about $5.4$ orders of magnitude greater than that of the blood.
Approximately $\$1985.06$
Approximately $\$30,067.29$
First find the decay constant: $25 = 50e^{5.27k} \Rightarrow k = \frac{\ln{\frac{1}{2}}}{5.27} \approx -0.1315$. when $90%$ decays, remaining amount is $10%$ of the initial amount, that is $0.1 \times 50 = 5$ grams. Substituting in the equation, $5 = 50e^{-0.1315t} \Rightarrow t \approx 17.51$ years.
$(a)$ $D(0)=15.$ So,the tumor was $15$ millimeters in diameter when when it was first detected. $(b)$ The tumor doubles after $25$ days.
The object would have cooled to $140^0$ F in about 95 minutes.
As $t \rightarrow \infty$, $i(t)=2 - 2e^{-\infty} \Rightarrow t = 2$ amps.
$(a)$ Population of the town was approximately $29$ million in $2010$. $(b)$ In $2013$, the population was approximately 32 million. $(c)$ Population would reach $60$ million in approximately $23$ years.
$(a)$ $A(t)=Ne^{-\left(\frac{\ln{2}}{5730}\right)} \approx Ne^{-0.00012097t}$. $(b)$ $A(20,000) \approx 0.088978 \times N$. So, about $8.9% remains. $(c)$ $t \approx $7171$ years.
Compounded quarterly means $n = 4$. So $3000 = 1000\left(1+\frac{0.12}{4}\right)^{4t}$. Answer: 9.3 years.
The equation to be used is $A=0.2(2)^{\frac{4\times60}{20}}$. Answer: $819.2$ milligrams.
Equation to be used: $15(1+r)^15 = 150$. Answer: $r \approx 17%$.
Approximately $94.1%$
Equation to be used: $40 = 5(0.5)^{-\frac{12}{k}}$. Answer: $4$ minutes.
Equation to be used: $3N = N(2)^{\frac{t}{5}}$. Answer: Approximately $7.9$ hours.