Dr. Lalitha Subramanian
About the Author

Aksharam
We observed in the previous module that the exponential function $f(x)=b^x$, for a real number $b$ with $0 \lt b \neq 1$ is either increasing (when $b \gt 1$) or decreasing (when $0 \lt b \lt 1$). This means that it is a one-to-one function. So, inverse function exists.This inverse function is called the logarithmic function. Now, we shall discuss the definition and properties of this inverse function.
Definition of logarithmic expression: for any value of $n \gt 0$ and $0 \lt b \neq 1$, the expression $m = \log_{b}{n}$ implies $n=b^m$, and vice versa.
Rewrite each of the following exponential expressions as logarithmic expressions:
$(a)$ $2^4=16$
$(b)$ $25^{\frac{1}{2}}=5$
$(c)$ $\left(\frac{1}{3}\right)^3=\frac{1}{27}$
Solution:
$(a)$ $2^4=16 \Rightarrow \log_{2}{16}=4$
$(b)$ $25^{\frac{1}{2}}=5 \Rightarrow \log_{25}{5}=\frac{1}{2}$
$(c)$ $\left(\frac{1}{3}\right)^3=\frac{1}{27} \Rightarrow \log_{\frac{1}{3}}{\frac{1}{27}}=3$
Rewrite each of the following logarithmic expressions as exponential expressions:
$(a)$ $\log_{4}{16}=2$
$(b)$ $\log_{2}{64}=6$
$(c)$ $\log_{c}{x}=p$
Solution:
$(a)$ $\log_{4}{16}=2 \Rightarrow 4^2=16$
$(b)$ $\log_{2}{64}=6 \Rightarrow 2^6=64$
$(c)$ $\log_{c}{x}=p \Rightarrow c^p=x$
Let $f(x) = b^x$ be an exponential function. As this function is one-one, inverse of this function exists. To find its inverse, we first interchange $x$ and $y$: \begin{eqnarray} f(x) &=& b^x\\ y &=& b^x\\ x &=& b^y\\ \end{eqnarray}
Then, we solve for $y$ using the definition of logarithmic expression: \begin{eqnarray} y &=& \log_{b}{x}\\ f^{-1}(x) &=& \log_{b}{x}\\ \end{eqnarray}
Definition of logarithmic function: For any value of $x \gt 0$ and $0 \lt b \neq 1$, $y = \log_{b}{x}$ if and only if $b^y = x$.
Basic properties of logarithms:
we can evaluate logarithmic expressions using the above properties. Below are some examples:
Evaluate each of the expressions:
$(a)$ $\log_{3}{81}$
$(b)$ $\log_{5}{\sqrt{5}}$
$(c)$ $\log_{2}{4\sqrt{2}}$
$(d)$ $\log_{0.5}{0.125}$
$(e)$ $6^{\log_{6}{5}}$
Solution:
$(a)$ $\log_{3}{81} = \log_{3}{3^4} = 4$
$(b)$ $\log_{5}{\sqrt{5}} = \log_{5}{5^{\frac{1}{2}}} = \frac{1}{2}$
$(c)$ $\log_{2}{4\sqrt{2}} = \log_{2}{2^{\frac{5}{2}}} = \frac{5}{2}$
$(d)$ $\log_{0.5}{0.125} = \log_{0.5}{0.5^3} = 3$
$(e)$ $6^{\log_{6}{81}} = 81$
Logarithms of two types are of importance and have many real life applications.
Graphs of logarithmic functions are basically reflections of the graphs of the corresponding exponential functions on the identity line $y=x$. as these are inverse functions. The graphs shown below illustrate $(1)$ Graphs of natural exponential and logarithmic function; and $(2)$ Graphs of common exponential and logarithmic functions. From the graphs we observe that logarithmic function is defined for only positive real numbers. This means that $\log_{b}(x)$ does not exist for any $x \in (-\infty, 0]$.
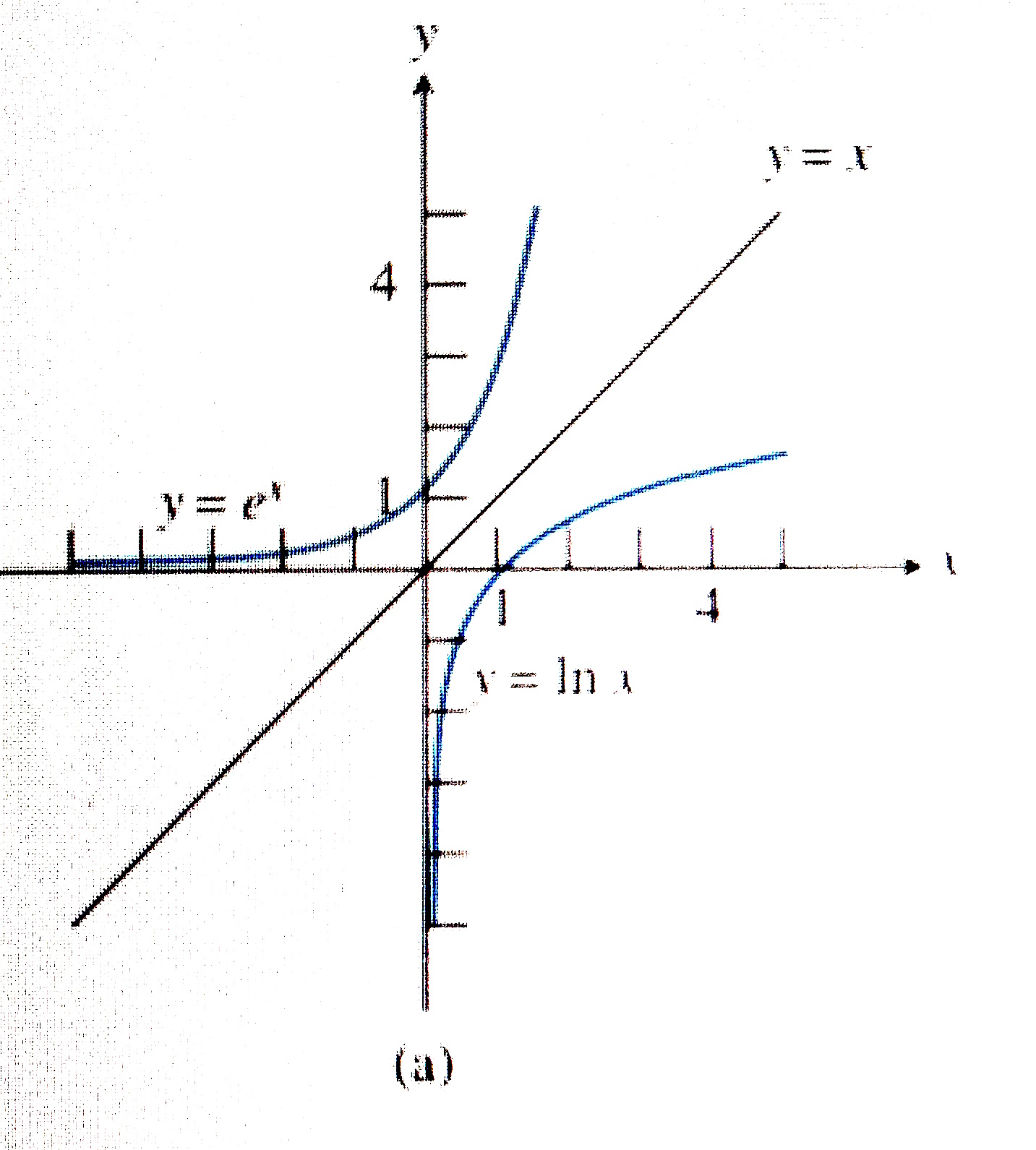
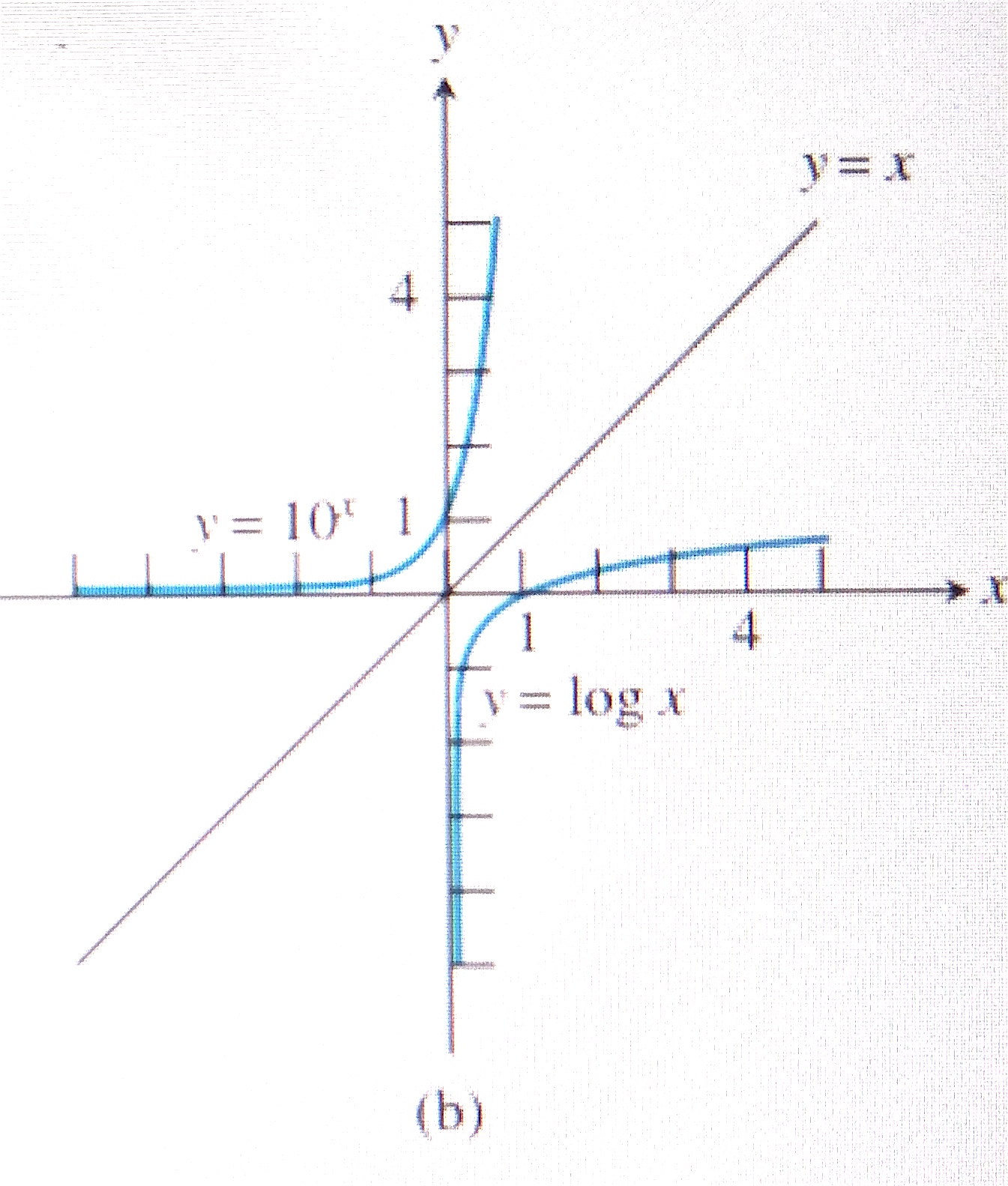
Properties of the graphs of logarithmic functions:
Graph of any logarithmic function can be obtained using transformations of the basic logarithmic function of the same base. Examples of some of these are provided below, taken from the textbook:
Evaluate:
$(a)$ $f(x)=3\log{x}$
$(b)$ $f(x)=1+\log{x}$
$(c)$ $g(x)=\ln{(x+2)}$
$(d)$ $g(x)=\ln{(3-x)}$
Solution:
$(a)$ Graph of $f(x)=3\log{x}$ is obtained by vertically stretching the graph of $y = \log{x}$ by a scale
factor of $3$ units.
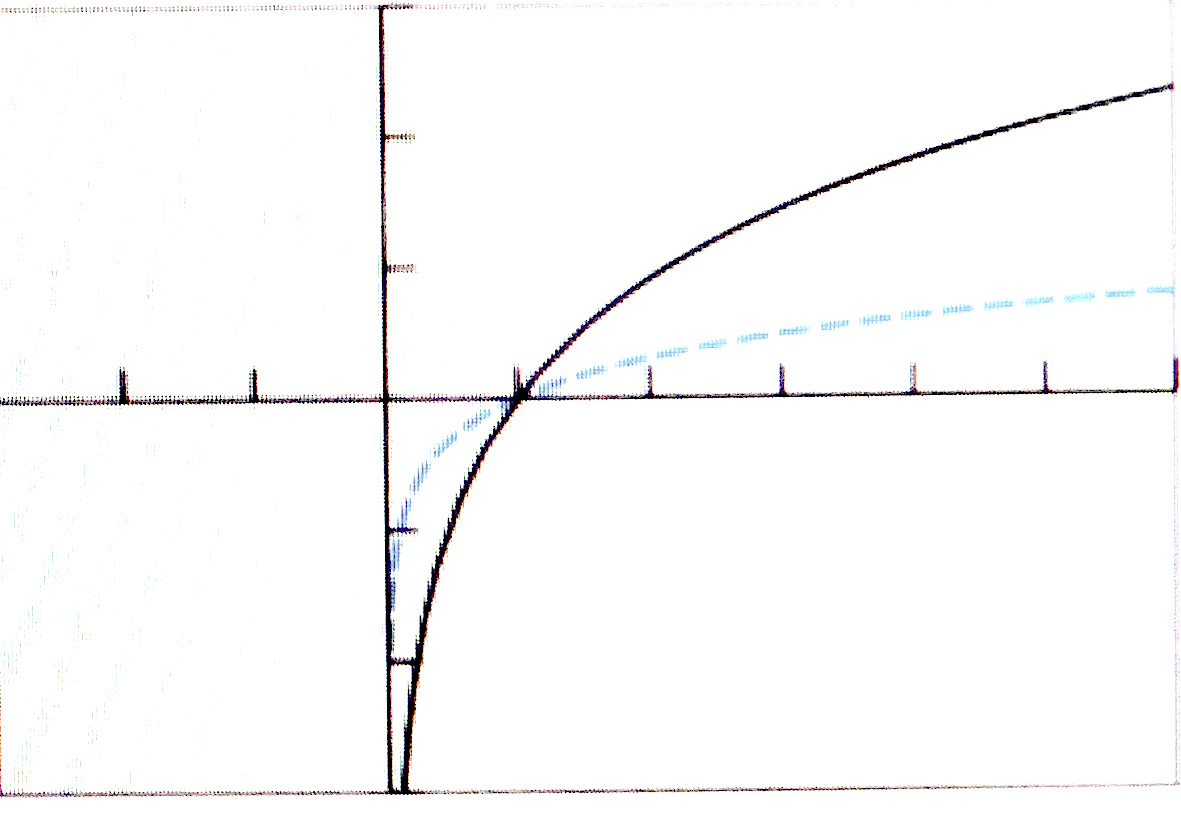
$(b)$ Graph of $f(x)=1+\log{x}$ is obtained by translating the graph of $y = \log{x}$ up by $1$ unit.
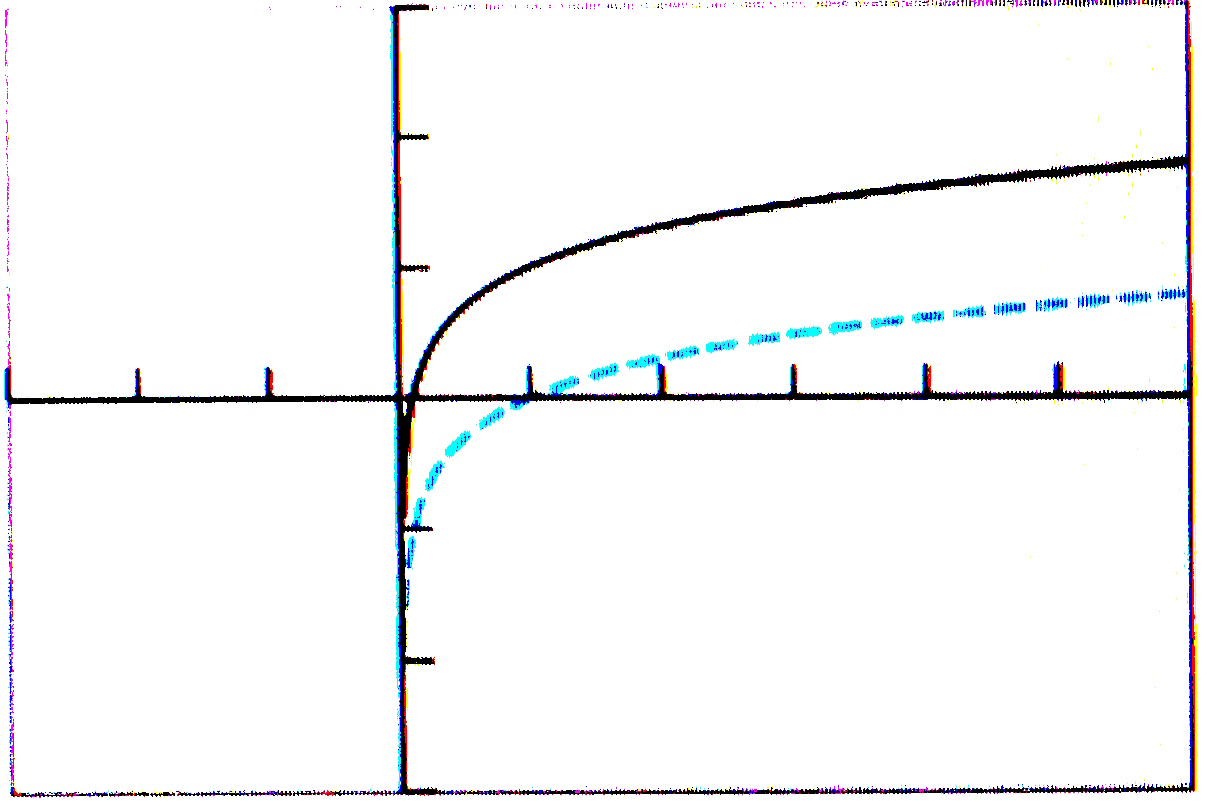
$(c)$ Graph of $g(x)=\ln{(x+2)}$ is got by translating the graph of $y = \ln{x}$ horizontally to the left by $2$ units.
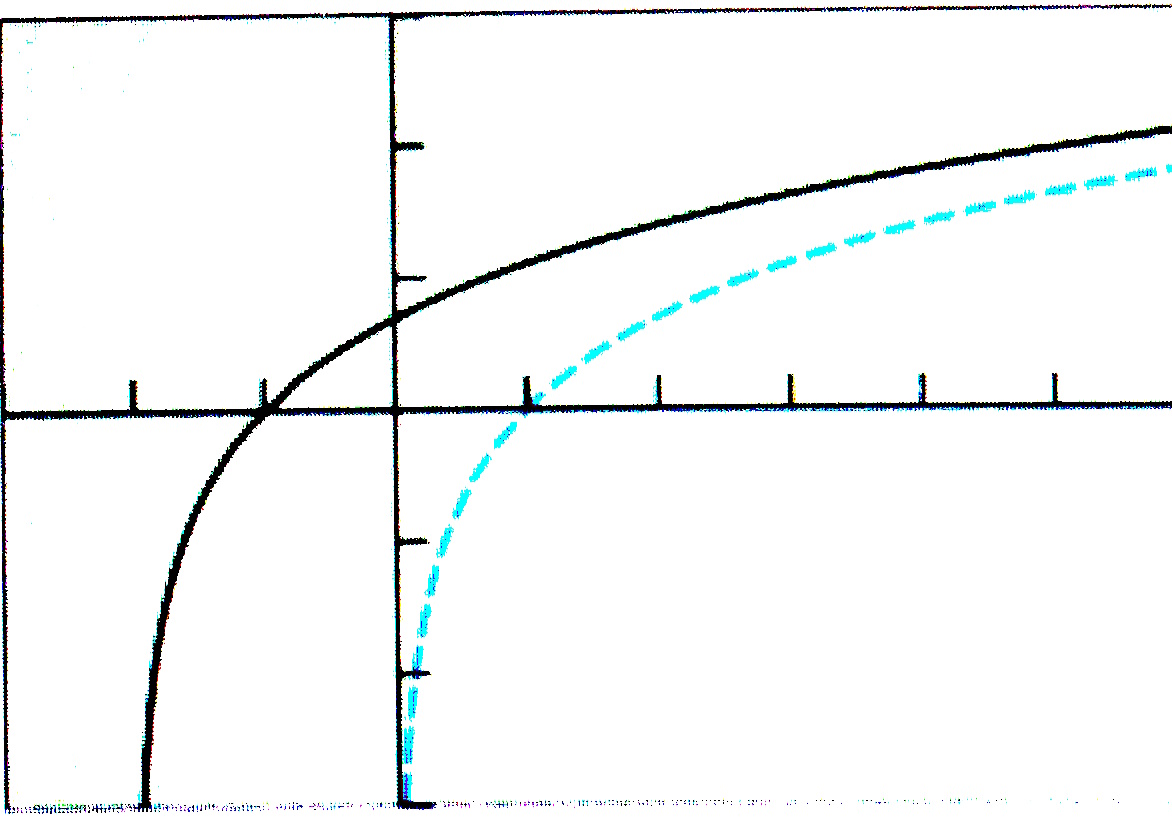
$(d)$ $g(x)=\ln{(3-x)}$ can be rewritten as $g(x)=\ln{[-(x-3)]}$. So, the graph of $g(x)=\ln{(3-x)}$ is obtained from the basic graph of $y=\ln{x}$ by
first reflecting it on the $y$-axis, and then translating horizontally to the right by $3$ units. 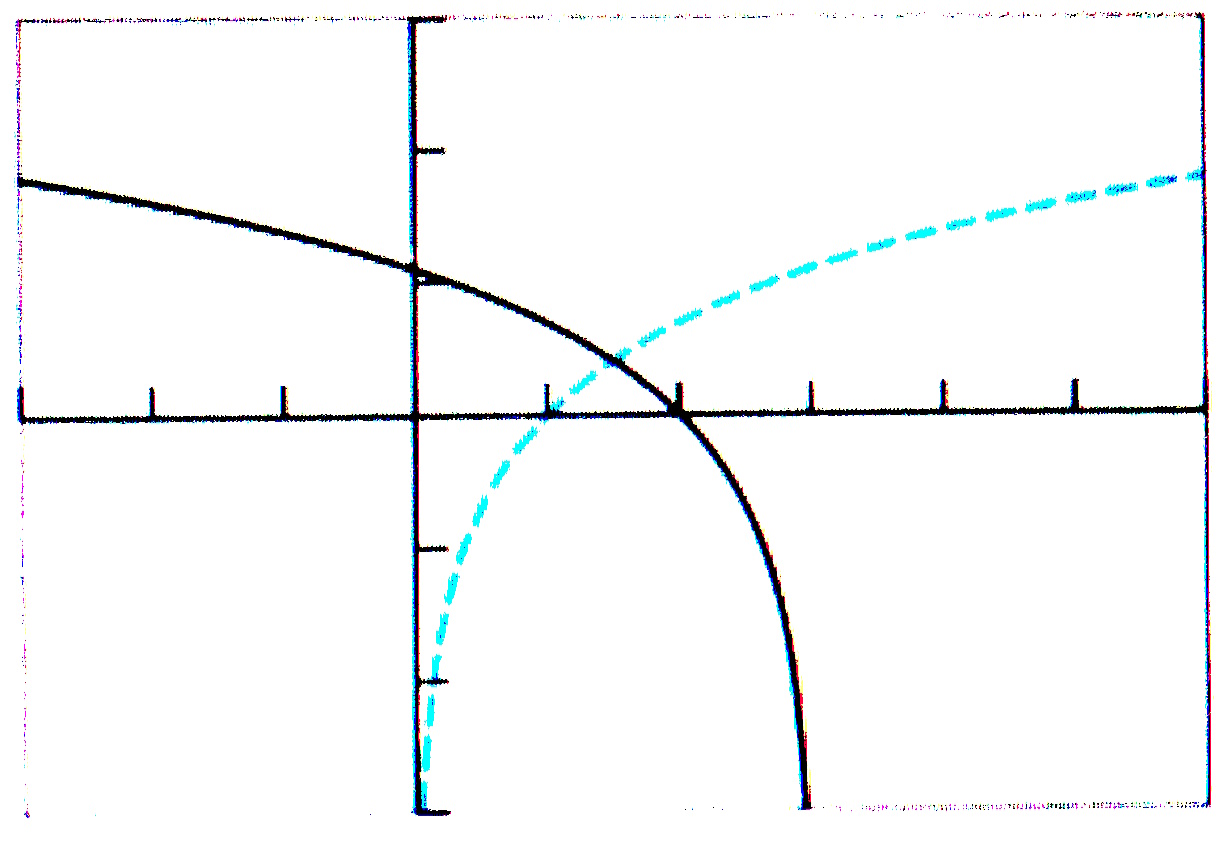
As logarithmic functions are not defined for non-positive real numbers, domain of an logarithmic function $f(x)=\log_{b}{x}$ is all real numbers $x \gt 0$. This is true for any logarithmic function obtained by transformation of the basic logarithmic functions.
Determine the domain of the following functions:
$(a)$ $f(x)= \log_{4}{(x+2)}$
$(b)$ $g(x)=\log{(x^2+9x+18)}$
$(c)$ $h(x)=ln{(3x-12)}$
Solution:
$(a)$ Domain of $f(x)= \log_{4}{(x+2)}$ is determined by setting $(x+2) \gt 0$ \begin{eqnarray} x+2 &\gt& 0\\ x &\gt& -2\\ \end{eqnarray} So, domain is $(-2, \infty)$.
$(b)$ $g(x)=\log{(x^2+9x+18)}$: To find the interval in which the domain of the function lies, we first need to find the critical points by setting the inside expresion to zero and solving: \begin{eqnarray} x^2 +9x+18 &=& 0\\ (x+3)(x+6) &=& 0\\ x = -3 \quad or \quad x = -6\\ \end{eqnarray} Using test value for the intervals $(-\infty, -6)$, $(-6, -3)$, and $(-3, \infty)$, we find that the domain is the set of all real numbers $x \in (-\infty, -6) \cup (-3, \infty)$.
$(c)$ Domain of $h(x)=ln{(3x-12)}$ is got by setting $3x-12$ greater than zero and solving: \begin{eqnarray} 3x-12 &\gt& 0\\ 3x &\gt& 12\\ x &\gt& 4\\ \end{eqnarray} So, domain is all real numbers $x \in (4, \infty)$.
Calculators have two keys that enable evaluation of exponential and logarithmic expressions.
Whenever calculator is used to evaluate logarithmic expressions, we approximate the answer to four decimal places.
Evaluate each expression using calculator:
$(a)$ $\log{26}$
$(b)$ $\ln{8}$
$(c)$ $\log_{5}{15}$
Solution:
$(a)$ $\log{26} =1.4150$
$(b)$ $\ln{8}=2.0794$
$(c)$ $\log_{5}{15} = \frac{\log{15}}{\log{5}}=1.6826$
Simple logarithmic equations can be performed by rewriting it in exponential form. The example below illustrates this process.
Solve each equation by changing it into exponential form:
$(a)$ $\log_{2}{x}=6$
$(b)$ $\log_{x}{64}=3$
$(c)$ $\log_{5}{\sqrt{125}}=x$
$(d)$ $log{x}=2$
Solution:
$(a)$ $\log_{2}{x}=6 \Rightarrow x=2^6$ So, $x = 64$
$(b)$ $\log_{x}{64}=3 \Rightarrow x^3=64$. So, $x = 4$
$(c)$ $\log_{5}{\sqrt{125}}=x \Rightarrow 5^x = \sqrt{125}$. So, $x=3$
$(d)$ $log{x}=2 \Rightarrow 10^2=x$. So, $x=2$
One of the very important properties of inverse functions is that their composition is the identity function. This means that, for any one-to-one function $f(x)$, we have $f \circ f^{-1}(x) = x$. The following example illustrates this.
Verify that the functions $f(x) = 3^x$ and $g(x) = \log_{3}{x}$ are inverse functions.
Solution:
Composite of $f(x)$ and $g(x)$: \begin{eqnarray} f \circ g(x) &=& f[g(x)]\\ &=& 3^{\log_{3}{x}}\\ &=& x\\ \end{eqnarray}
So, $f(x)$ and $g(x)$ are inverse functions.
Evaluate each exponential expression given in problem #1 - 5 into logarithmic expressions:
$\log_{5}{25}=2$
$\log_{2}{64}=6$
$\log {100,000}=5$
$\log_{0.3}{0.9}=2$
$\ln{f}=d$
Rewrite each expression from problem # 6 - 10 as exponential expression:
$x^a=b$
$10^{xz}=y$
$e^{\frac{1}{y}}=x$
$2^3=8$.
$10^{pq}=x^2y$
Evaluate each expression from problem $11 -18 without use of a calculator:
$\log{1000} = \log_{10}{10^3} = 3$
$\log_{6}{\sqrt{36}} = \log_{6}{6^{\frac{1}{2}}} = \frac{1}{2}$
$\log_{3}{\sqrt[4]{27}} = \log_{3}{3^{\frac{3}{4}}} = \frac{3}{4}$
$\log{\frac{1}{100000}=\log_{10}{10^{-5}}} = -5$
$\ln{\frac{1}{\sqrt[5]{e}}} = \log_{e}{e^{-\frac{1}{5}}} = -\frac{1}{5}$
$\ln{e^{-8}} = \log_{e}{e^{-8}} = -8$
$10$
$18$
Evaluate each problem from #19 - 22 using calculator:
$1.1370$
Not defined.
$1.6355$
$1.2928$.
Solve each of the equations from problem #23 - 27 by changing it into exponential form:
$x=10^4 \Rightarrow x = 10000$
$x=10^{-2} \Rightarrow x = \frac{1}{100}$
$x^4=81 \Rightarrow x =3$
$x=5^4 \Rightarrow x=625$
$x=10^{\frac{1}{2}} \Rightarrow x = \sqrt{10}$
For problems #28 - 30, describe the transformation to be done and the basic function on which the transformations are to be done. Then sketch the graph of the basic function and all the transformations.
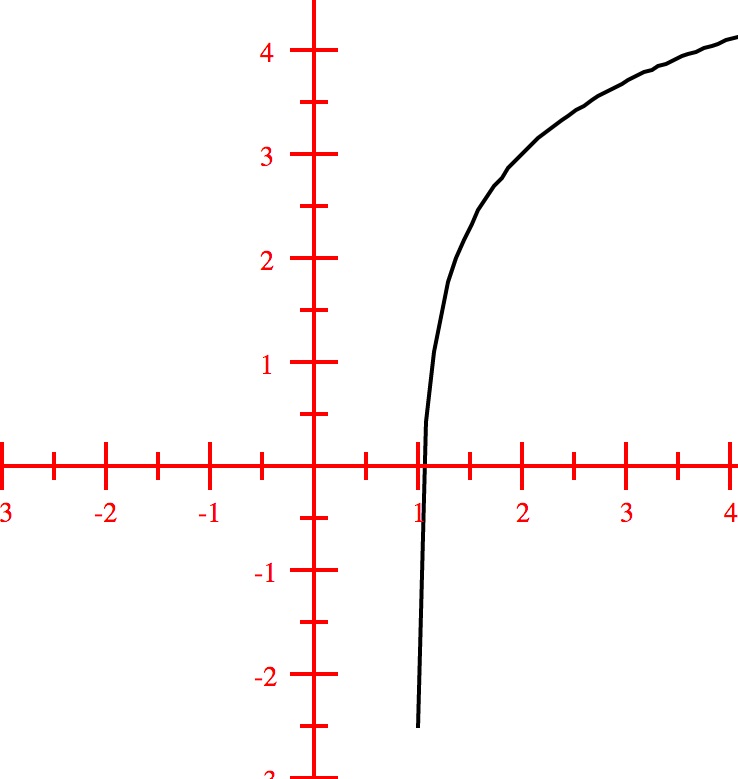
$(1)$ Basic function is $y = \log(x)$. Black curve in the graph below. $(2)$ Horizontal translation to the right by $1$ unit. Blue curve in the graph below. $(3)$ Vertical translation upwards by $3$ units. Thick brown curve in the graph below.
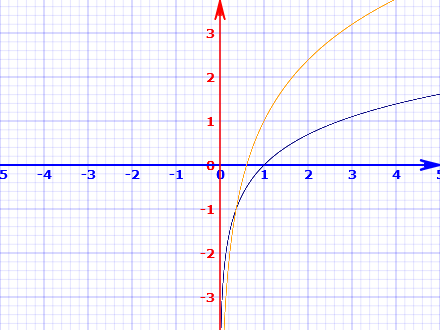
$(1)$ Basic function is $y = \ln{x}$. Black curve in the graph below. $(2)$ Horizontal translation to the left by $1$ unit. Blue curve in the graph below. $(3)$ Vertical stretch by a scale factor of $2$ units. Thick brown curve in the graph below.
$(1)$ Basic function is $y = \log{x}$. Black curve in the graph below. $(2)$ Reflection on $y$- axis. Blue curve in the graph below. $(3)$ Vertical translation downwards by $1$ unit. Thick brown curve in the graph below.
\begin{eqnarray} f \circ g(x) &=& f[g(x)]\\ &=& \log_{2}{2^x+1-1}\\ &=& \log_{2}{2^x}\\ &=& x\\ \end{eqnarray} Hence $f(x)$ and $g(x)$ are inverse functions.
\begin{eqnarray} f \circ g(x) &=& f[g(x)]\\ &=& e^{\ln{(x+3)}-1+1} -3 \\ &=& e^{\ln{x+3}} -3\\ &=& x +3 - 3\\ &=& x\\ \end{eqnarray} So $f(x)$ and$g(x)$ are inverse functions.
Domain is all real numbers $x \in (-2, -1) \cup (1, \infty)$
All real numbers $x \in (-\infty, \infty)$
All real numbers $x \in (13, \infty)$