Dr. Lalitha Subramanian
About the Author

Aksharam
We reviewed problem solving process at the end of Chapter P, and also discussed some application problems involving linear equations. In this section, we discuss application problems involving polynomial and rational functions.
The most important and basic application of functions is the rate of change of the dependent variable with respect to the independent variable.
To elucidate, let us take the simplest polynomial - a linear polynomial $y = f(x) = mx + b$. We know that $y$ is the function value, which we refer to as the dependent variable, and $x$ is the independent variable. Graph of a linear function is a straight line. The slope of the line $m$ is also the rate of change of $y$ with respect to $x$. That is, the average rate of change of the function between $x = a$ and $x = b$, $a \neq b$ is given by the ratio of change in $y$ value to the change in $x$ value between the points $(a, f(a))$ and $(b, f(b))$. This is written in formula form as $$m = \frac{rise}{run} = \frac{change-in-y}{change-in-x} = \frac{f(b)-f(a)}{b-a} = \frac{\Delta{y}}{\Delta{x}}$$
As a straight line has uniform slope, the rate of change of $y$ with respect to $x$ is constant between any two distinct points on the line. Hence, average of rate of change is the same as the rate of change in case of a straight line.
Any function other than linear function has a variable slope. So, the rate of change of $y$ with respect to $x$ varies between two points. Hence the concept of average rate of change.
The value of a housing complex is $\$5,000,000$ currently. It is depreciating at the rate of $\$20,000$ every year.
$(a)$ What is the rate of change of the value of the complex?
$(b)$ Write an equation for the value of the complex $v(t)$ as a linear function of $t$.
$(c)$ Evaluate $v(5)$ and interpret your results.
$(d)$ When will the value of the complex be $\$3,600,000$?
Solution:
$(a)$ As the value of the complex depreciates at the rate of $\$20,000$ per year, rate of change is $-20,000$.
$(b)$ Taking the current value as the initial value, at $t = 0$, This value is equivalent to the $y$-intercept of the graph of the function. So, the required linear equation is $$v(t) = -20,000t + 5,000,000$$.
$(c)$ Substituting $t = 5$ in the equation: \begin{eqnarray} v(5) &=& -20,000(5) + 5,000,000\\ &=& -100,000 + 5,000,000\\ &=& 4,990,000\\ \end{eqnarray}
The value of the complex after 5 years is $$4,990,000$.
$(d)$ Substituting $v = 3,600,000$ and solving for $t$: \begin{eqnarray} 3,600,000 &=& -20,000t + 5,000,000\\ 20,000t &=& 5,000,000 - 3,600,000\\ 20,000t &=& 1,400,000\\ t &=& 70\\ \end{eqnarray}
The value of the housing complex becomes $\$3,600,000$ in $70$ years.
A quadratic function is typically used to model situations and to predict the maximum or minimum possible value of a particular quantity. We know that a quadratic function $f(x) = ax^2 + bx + c$ attains maximum or minimum at its turning point according as $a \lt 0$ or $a \gt 0$, respectively. Moreover, we also know that the coordinates of the turning point $(h,k)$ can be computed by the formula $h = -\frac{b}{2a}$ and $k = f(h)$. These and other properties of graphs of quadratic functions are used to model real-life problems.
One of the major applications of quadratic functions are profit and loss analyses in economics. While working out these problems we shall keep in mind the following aspects of economic functions:
Twin Cereal company modeled their weekly demand of breakfast cereal as $y = = -12.5x + 75$ Using this model, develop a model for weekly revenue of the company in thousands of dollars. Determine the maximum revenue and the number of items to be produced for attaining the maximum revenue.
Solution:
Revenue function is \begin{eqnarray} R(x) &=& xy\\ &=& x(-12.5x + 75)\\ &=& - 12.5x^2 + 75x\\ \end{eqnarray}
The coefficient of $x^2$ is negative. So, the turning point $(h,k)$ of the graph of this function is a maximum point. Computing the $(h,k)$: \begin{eqnarray} h &=& -\frac{-75}{2(-12.5)}\\ &=& 3\\ k &=& -12.5(3)+75\\ &=& 37.5\\ \end{eqnarray}.
Answer: Maximum weekly revenue of $\$37,500$ and it is obtained at the production level of $3$ items per week.
The cost, in dollars, to produce $x$ shirts by a certain factory is given by $C(x) = 2x + 26$, $x \geq 0$. The price-demand function, in dollars per shirt is $p(x) = 30 - 2x$, $0 \leq x \leq 15$.
$(a)$ Find and interpret $C(0)$.
$(b)$ Find and interpret $\overline{C}(10)$.
$(c)$ Find and interpret $p(5)$.
$(d)$ Find and simplify $R(x)$.
$(e)$ Find and simplify $P(x)$.
$(f)$ Solve $P(x)=0$ and interpret.
Solution:
$(a)$ $C(0) = 26$. The fixed costs are $26$.
$(b)$ $\overline{C}(10) = 4.6$. When 10 shirts were produced, the cost per shirt is $\$4.60$.
$(c)$ $p(5) = 20$. To sell 5 shirts, the price per shirt should be set at $20 per shirt.
$(d)$ $R(x) = -2x^2 + 30x, \quad 0 \leq x \leq 15$.
$(e)$ $P(x) = -2x^2 + 28x - 26, \quad 0 \leq x \leq 15$.
$P(x) = 0$ when $x = 1$ and when $x = 13$. These are the break-even points. So, selling $1$ or $13$ shirts will guarantee the revenue exactly equals the production cost.
Another major application of polynomial functions involves motion of a particle. In particular, we shall discuss vertical free fall motion and projectile motion. Any object that is dropped vertically down from a height or thrown vertically up experiences a downward acceleration due to gravity $g$, which approximately equals $9.8 m / sec^2$ or $32 ft/sec^2$. Its velocity at a given time $t$ is given by the formula $v(t)=-gt+v_0$ and its height at any given time $t$ is given by the formula $s(t)=-\frac{1}{2}gt^2+v_0t+s_0$, where $t$ is the time in seconds, $v_0$ is the initial velocity, and $s_0$ is the initial height.
A baseball throwing machine is used to train boys to catch high pop-ups. It throws the baseball straight up with an initial velocity of $48$ ft/sec from a height of $3.5$ ft.
$(a)$ Find an equation that models the height of the ball $t$ seconds after it is thrown.
$(b)$ What is the maximum height the baseball will reach? How many seconds will it take to reach that height?
Solution:
Given that initial height is $s_0 = 3.5$ and initial velocity is $v_0=48$. Substituting these values and the value of $g = 32$ in the equation, we get: \begin{eqnarray} s(t) &=& - \frac{1}{2}(32)t^2 + 48t + 3.5$\\ &=& -16t^2+ 48t+3.5\\ \end{eqnarray}
$(b)$ Vertex of this quadratic function gives the maximum value as the leading coefficient is negative. So, we shall find the coordinates $(h,k)$ of the vertex: \begin{eqnarray} h &=& \frac{-48}{2(-16)}\\ &=& \frac{3}{2}\\ &=& 1.5\\ k &=& -16(1.5)^2 + 48(1.5) + 3.5\\ &=& 39.5\\ \end{eqnarray}
Answer: The ball will reach maximum height of $39.5$ feet in $1.5$ seconds.
Polynomial and rational functions are frequently used in application problems involving proportions or variations. While doing these problems we need to keep in mind that, when a particular variation is given, this can be written as an equation by multiplying the right side by a constant of variation $k$. Then, we can solve the problem using the equation.
Volume of a sphere varies directly as the cube of its radius. When the radius is $2$ feet, volume of the sphere is $33.49$ cubit feet. Find the radius of a sphere whose volume is $113.04$ cubit feet.
Solution:
First write the variation specified in the problem: $$ V \infty r^3$$. Then, write the variation as an equation by multiplying the right side by the constant of variation: $$ V = kr^3$$. Now, use the set of given information to find the constant $k$: \begin{eqnarray} 33.49 &=& k(2)^3\\ 33.49 &=& 8k\\ \frac{33.49}{8} &=& k\\ 4.187 &=& k\\ \end{eqnarray}
Rewrite the equation of variation with the value of $k$: $$ V = 4.187r^3$$. Now, substitute the value of the volume to determine the radius: \begin{eqnarray} V &=& 4.187r^3\\ 113.04 &=& 4.1876r^3\\ 27 &=& r^3\\ 3 &=& r\\ \end{eqnarray}
Answer: When the volume of the sphere is $113.04$ cubic feet, its radius is $3$ feet.
Apart from the above specific applications, polynomials are widely used to model and solve many real life situations. Some of them are discussed in the following examples.
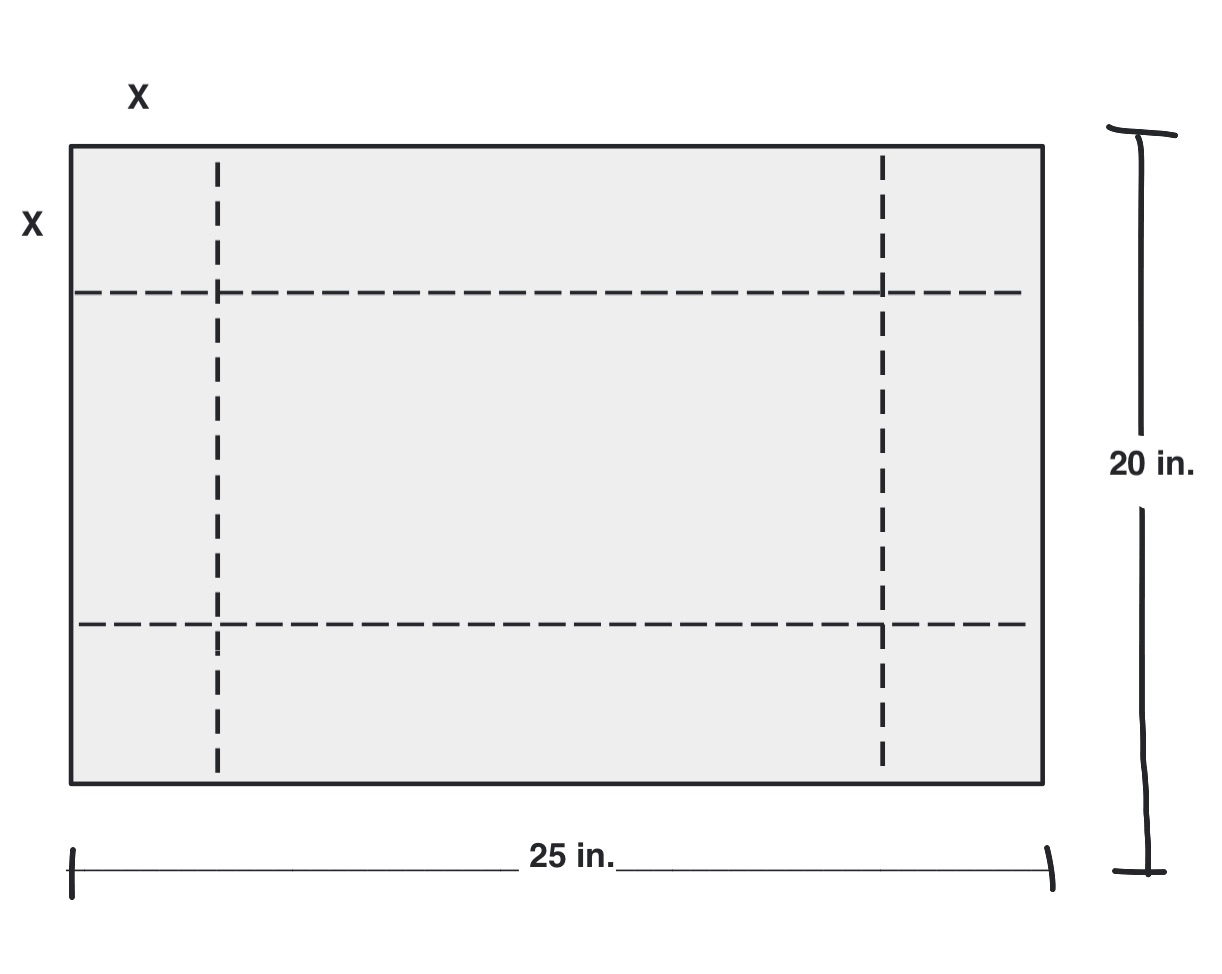
A rectangular open box is to be made by removing squares of equal width $x$ from the corners of a $20$ inch by $25$ inch rectangular cardboard. Determine the width of the squares $x$ to be cut so that the volume of the box is at least $798$ cubic inches.
Solution:
From the diagram, note that the height of the box is $x$, the length is $(25-2x)$, and the width is $(20-2x)$. The volume of the box is given by the equation $V = x(25-2x)(20-2x)$. As the width of the cardboard is $15$ inches, the value of $x$ should be less than half of it.That is the domain of $x$ is $0 \leq x \leq 10$ The requirement that the volume should be at least $798$ is satisfied by the inequality $ x(25-2x)(20-2x) \geq 7989$. Now, solving the inequality: \begin{eqnarray} x(25-2x)(20-2x) & \geq 798\\ x(500-90x+4x^2) &\geq 798\\ 4x^3 - 90x^2 + 500x -798 &\geq 0\\ \end{eqnarray}
By trial and error method, we find that $x = 3$ is the only real solution in the domain of $x$.
Sign chart for this value shows that the solution set is $x \geq 3$. Hence we conclude that the volume of the box would be at least $798$ cubic inches then
the width of the squares to be cut is $3$ inches.
Pump A can empty a tank full of water in 30 hours and pump B can an empty this tank in 24 hours. How long will it take to empty the tank if both pumps are used simultaneously?
Solution:
Let the time taken by both pumps working together to empty the tank be $t$ hours. Pump A can do the work in $30$ hours. So, in 1 hour, pump A can do $\frac{1}{30}$ of the work.. Thus, portion of the work done by pump A in $t$ hours is $\frac{t}{30}$ hours. Pump B can do this work in $24$ hours. So, in 1 hour, pump B can do $\frac{1}{24}$ of the work. Thus, portion done by pump B in $t$ hours is $\frac{t}{24}$ of the work. So, the required equation is obtained by adding the portions of work done by pumps A and B and setting it equal to 1, as they empty the tank in $t$ hours. Solving this equation: \begin{eqnarray} \frac{t}{30} + \frac{t}{24} &=& 1\\ \frac{4t + 5t}{120} &=& 1 \\ 9t &=& 120\\ t &=& \frac{120}{9}\\ &=& \frac{40}{3}\\ &=& 13\frac{1}{3} \\ \end{eqnarray}
Answer: It takes 13 hours and 20 minutes for both pumps, working together, to empty the tank.
A company manufacturing glasses determines that the supply and demand for their product are $S = 200 - p + 0.000007p^4$ and $D = 1500 - 0.0004p^3$, where $p$ is the price of one unit. Determine the price for which the supply equals the demand and the number of units corresponding this equilibrium price.
Solution:
By using trial and error method or by using calculator, we find the the supply and demand function are equal for $p \approx 107$ is the only real solution. This means that the equilibrium price is approximately $\$ 107$ per unit. The number of units corresponding to this equilibrium price is obtained by substituting this value in either of the above functions: \begin{eqnarray} S &=& 200 - 107 + 0.000007(107)^4\\ & \approx & 1010\\ \end{eqnarray}
Answer: Equilibrium price is approximately $\$ 107$ per unit. The number of unit corresponding to this equilibrium price is approximately 1010 units.
Some of the application problems for rational functions include percentage problems, rate problems, distance-speed problems, etc. Some common examples are discussed below:
How much pure acid must be added to $50$mL of a $35\%$ acid solution to produce a mixture of $75\%$ acid?
Solution:
While doing such "mixture" problems, important point to keep in mind is the basic idea of percentage. That is, actual value = (Percentage in decimal) x (Total amount of the mixture). In the context of this problem, we have "the amount of pure acid in $50$mL of $35\%$ solution is $0.35 \times 50 = 17.5$ mL. Makin a table as below would help understand and form the equation required to solve the problem.
\begin{array}{cccc} Solution & Amount & Percentage & Amount of acid\\ \hline I & 50 mL & 35\% & 17.5mL\\ II & x mL & 100\% & x \\ Mixture & (50+x) mL & 75\% & (17.5 +x) \\ \hline \end{array}
the last row states that the total quantity of the mixture is $(50 + x)$ mL has a $75\%$ concentration of acid. the last entry shows the amount of acid in the concentration is $(17.5+x)$ mL. Setting up an equation and solving, we get, \begin{eqnarray} (50+x) \times 0.75 &=& 17.5 + x\\ 37.5 + 0.75x &=& 17.5 + x\\ 20 &=& 0.25x\\ x &=& 80\\ \end{eqnarray}
Answer: $80$ mL of pure acid is to be mixed with $50$ mL of $35\%$ acid to make a mixture of $75\%$ acid.
Below are some typical examples of application problems involving inequalities:
The area $A$ in square inches, of a square piece of a plywood board which measures $x$ is $A(x)=x^2$. Suppose a manufacturer needs to produce a $24$ inch by $24$ inch square piece of plywood board from this board, how close does the side of the piece need to be cut to $24$ inches to guarantee that the area of the piece is within a tolerance of $0.25$ square inches of the target area of $576$ square inches?
Solution:
The inequality that expresses the desired area as within $0.25$ square inches of $576$ as $|A-576| \leq 0.25$. Solving this absolute value inequality: \begin{eqnarray} -0.25 &\leq& x^2 - 676 & \leq& 0.25\\ 575.75 &\leq& x^2 &\leq& 576.25\\ \sqrt{575.75} &\leq& x &\leq& \sqrt{576.25}\\ \end{eqnarray}
Using a calculator, we conclude that the side of the piece should be cut between $23.995$ inches and $24.005$ inches approximately.
Working alone, $A$ can perform a work in $4$ hours. If $B$ helps, they can finish the same work in $3$ hours. How long would it take $B$ to finish the work if he does it alone?
Solution:
The key relationship between work done, and time taken is
Amount of work done = Rate of work x time spent
$A$ completes the work alone in $4$ hours. So, rate of $A$'s work is $\frac{1}{4}$ per hour. Let us assume $B$ completes the work alone in $t$ hours. Then, $B$'s rate of work is $\frac{1}{t}$ per hour. Both $A$ and $B$ together completes the work in $3$ hours. This means that the rate of completing the work together is $\frac{1}{4} + \frac{1}{t} = \frac{1}{3}$. Solving this equation for $t$:
\begin{eqnarray} \frac{1}{4}+\frac{1}{t} &=& \frac{1}{3}\\ \frac{1}{t} &=& \frac{1}{3}-\frac{1}{4}\\ \frac{1}{t} &=& \frac{1}{12}\\ t &=& 12\\ \end{eqnarray}
So, working alone, $B$ can finish the work in $12$ hours.
$S = kr^2$
$F = \frac{k}{d^2}$
He can make about $48$ dolls.
Maximum area would be for a square of side $25$ feet.
The yard is $11$ feet wide and $14$ feet long.
Width of the walkway is $3.73$ feet.
$3.87$ L
A windspeed of $80$ mph would generate $7680$ watts power.
$(a)$ More than $70$ units must be produced per week to make a profit. $(b)$ $170$ units must be produced in order to realize a profit of $\$6,000$.
The value os $x$ should less than $21.5$ or greater than $31$. that is , $x \in (0, 21.5] \cup [31, \infty)$
Supply equals demand when price of one item is $\$36.27$; Approximately $53.7$ items should be produced in order to achieve this equilibrium price.
Approximately $169.12$ mL of pure acid must ba added.
$(a)$ Average cost function $\overline{C}(x)=\frac{3000}{x}+2.00x$ $(b)$ The company should at least $667$ balls per week in order to make a profit.
Current tiger population in the reserve is $50$. $25$ years hence, the population would be $300$.
As the capacity of the can is $500$ mL, its volume is $500$ cubic centimeters. Using this, we find that $h = \frac{500}{\pi{x^2}}$. So, the function representing the curved surface area would be $S(x)=\frac{1000}{x}$
Time taken is the ratio of distance traveled and speed. Time taken to travel car is $\frac{17}{43+x}$ and time taken to travel by bike is $\frac{53}{x}$. So, the total time taken to travel from home to theater as a function of the speed $x$ is $T(x)=\frac{17}{43+x} + \frac{53}{x}$.
In order to earn a profit, minimum of $\$9091$ Candy bars would have to be sold.
$V(x)=-x^3\left(\frac{2\pi}{3}\right) + x^2(140\pi)$; When volume is $558$ cubic feet, radius of the container is $6$ feet.
$R_2=\frac{1.2x}{x-1.2}$; When $R_1 = 3$ ohms, $R_2 = 2$ ohms.
$(a)$ $C(0) = 36$. The daily fixed costs are $36$; $(b)$ $\overline{C}{10}=6.6$ When 10 pies afe made, the cost per pie is $\$6.60$; $(c)$ $p(5)=9.5$. To sell $5$ pies per day, set the price at $\$9.50$ per pie; $(d)$ $R(x)=-0.5x^2+12x$, $0 \leq x \leq 24$; $(e)$ $P(x)=-0.5x^2+9x-36$, $0 \leq x \leq 24$; $(f)$ $P(x)=0$ when $x=6$ and $x=12$. These are break-even points. Selling 6 pies or 12 pies a day will guarantee the revenue earned equal to the cost of production.
$W(x)=200+0.05x$, $x \geq 0$. She must make $\$5500$ in weekly sales.
Average rate of change is $-32$. During the first two seconds after it is dropped, the object has fallen at an average rate of $32$ feet per second.
$(a)$ $P(x)=-2x^2+120x-1000$, for $0 \leq x \leq 70$; $(b)$ $30$ bikes should be made and sold to maximize profit; $(c)$ The maximum monthly profit is $\$80,000$; $(d)$ The price per bike should be set at $\$8000$; $(e)$ The break-even points are $x = 10$ and $x=50$. To make a profit, between 10 and 50 bikes need to be mad and sold per month.
Make the vertex of the parabola $(0,10)$ so that the point on the top of the left-hand tower where the cable connects is $(-200, 100)$ and the point on the top of the right-hand tower is $(200,100)$. Then, the parabola has equation $f(x)= \frac{9}{4000}x^2+10$. Standing 50 feet to the right of the left-hand tower means you are standing at $x=-150$ and $f(-150)=60.625$. So, the cable is $60.625$ feet above the bridge deck there.
$P(x) \geq 50$ on the interval $[10,15]$. So, anywhere between $10$ and $15$ bottles should be sold in order to make at least $\$50$ profit.
Solving the inequality $T(t) \gt 42$ gives approximately $t \in (1.37,14.63)$. This corresponds to between $7:22$ AM and $8:38$ PM. Since the domain restriction stipulates $0 \leq t \leq 12$, we conclude that it is warmer than $42$ degree $F$ from $7:22$ AM to $6$ PM.
Making and selling $71$ game stations per week would yield a maximum profit of $\$5910.67$.
$(a)$ $C(5)=590$ means it costs $\$590$ to remove $25\%$ of dirt from the pond. $C(95)=33630$ means it costs $\$33630$ to remove $95\%$ dirt from the pond. $(b)$ The vertical asymptote $p=100$ means that as we try to remove $100\%$ of dirt from the pond, the cost increases without bound. This means that it is impossible to remove $100\%$ dirt from the pond. $(c)$ For $\$400000$, we can remove approximately $95.76\%$ of the dirt.
Three hours
The radius of the drum should be $\approx{1.05}$ feet and the height should be $\approx{2.12}$ feet.The minimum surface area should $\approx{20.93}$ square feet.