Dr. Lalitha Subramanian
About the Author

Aksharam

Precalculus

Chapter 2: Polynomial and Rational Functions

PDF Version

2-7: Solving Rational Inequalities in One Variable

An inequality of a rational function $f(x) = \frac{p(x)}{q(x)}$, where $p(x)$ and $q(x)$ are polynomials, can be written in any one of the following forms:

  1. $f(x) \gt 0$: Solutions of this inequality are values of $x$ that make $f(x)$ positive.
  2. $f(x) \geq 0$: Solutions of this inequality are values of $x$ that make $f(x)$ non-negative.
  3. $f(x) \lt 0$: Solutions of this inequality are values of $x$ that make $f(x)$ negative.
  4. $f(x) \leq 0$: Solutions of this inequality are value of $x$ that make $f(x)$ non-positive.
  5. $f(x) \neq 0$: Solutions of this inequality excludes only the values of $x$ that make $f(x) = 0$.

Based on the properties of multiplication and/or division of real numbers, we have the following guidelines to establish the sign of $f(x)$

Let $p(x) = (x-a)(x-b)...$ be the factored form of the numerator of $f(x)$. Then, sign of $p(x)$ can be determined by finding the sign of each of these factors using the multiplication rules: \begin{eqnarray} (+)(+) &=& (+)\\ (-)(-) &=& (+)\\ (+)(-) &=& (-)\\ (-)(+) &=& (-)\\ \end{eqnarray}

Example 1:

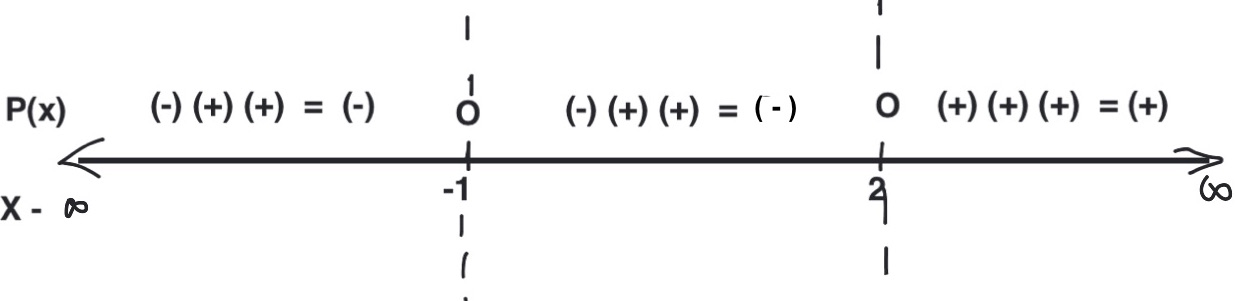
Find the intervals where the polynomial $P(x) = (x-2)(x+1)^2(x^2+3)$ is positive, negative, or zero.

Solution:First we find the zeros of this polynomial: Setting $P(x) = 0$, we get $x = 2$ and $x = -1$. Next, we can draw a real number line and partition it into three intervals $(-\infty, -1)$, $(-1, 2)$, and $(2, \infty)$, based on these zeros. Now, we can use a sign chart to determine the sign of the polynomial in each of these intervals. 2-7E1
Alternatively, we can prepare a table of the intervals, test values in each of these intervals, and the sign of the polynomial in each of these intervals: \begin{array}{ccc} Interval & Test-Value & Sign\\ \hline (-\infty, -1) & -2 & (-)(+)(+)=(-)\\ (-1, 2) & 0 & (-)(+)(+)=(-)\\ (2, \infty) & 3 & (+)(+)(+)=(+)\\ \hline \end{array}

We note that the polynomial is positive only in the interval $(2, \infty)$. So, we conclude:

$P(x) > 0$ in the interval $(2, \infty)$;
$P(x) = 0$ at $x = -1$ and $x = 2$;
$P(x) < 0$ in the intervals $(-\infty, -1)$ and $(-1, 2)$.

The above example also shows that the polynomial changes sign at its real zeros of odd multiplicity $(x = 2)$ and keeps the same sign at the real zeros of even multiplicity $(x = -1)$. This confirms that the graph of this polynomial crosses the $x$-axis at $x = 2$ and touches the $x$- axis at $x = -1$.

To solve a polynomial inequality, first find the zeros, which are called the critical points of the inequality. Then, partition the real number line into intervals, and determine the sign of the polynomial in each of the intervals. Select the interval that is appropriate for the given inequality to get the solution set in interval form.

Example 2:

Solve: $(x-1)^2(x+3)^3 \geq 0$

Solution:Critical points of the polynomial are got by setting it to zero: $x = 1$ and $x = -3$.
Now, to determine the intervals where the required inequality holds, we use sign chart, either using a real number line as in the previous example, or using a table as follows:

\begin{array}{ccc} Interval & Test Value & (x-1)^2(x+3)^3\\ \hline (-\infty,-3) & -4 & (+)(-) = (-)\\ (-3,1) & 0 & (+)(+) = (+)\\ (1, \infty) & 2 & (+)(+) = (+)\\ \hline \end{array}

The required inequality is true for the intervals where the last column shows (+) sign. Hence the answer to this problem is $x \in [-3, \infty)$. Note that, as this is an inclusive inequality, we include the critical points in the solution set.

Example 3:

Find the solution set of the inequality $x^4 - x^3 -12x^2 \lt 4x - 16$

Solution:First step in solving these types of problems are to bring all terms to left side, and set the right side to zero. Second step is find the zeros of the left side polynomial. These values given the critical points for the required inequality. Thirdly, create a sign chart either by using real number line (as shown in example 1) or by using a table (as shown in example 2), to determine the interval(s) where the inequality holds. Lastly, write your solution set, including or excluding the critical points as the inequality is inclusive or strict, respectively.These steps are illustrated below for the above inequality.

  1. Step 1: \begin{eqnarray} x^4 - x^2 - 12x^2 - 4x + 16 \lt 0\\ \end{eqnarray}
  2. Step 2: Using Rational Zeros Theorem, Factor Theorem, and synthetic division, we find that the zeros of this polynomial. They are $x = 1$ and $x = 4$, each with multiplicity 1, and $x = -2$, with multiplicity 2.
  3. Step 3: Create a sign chart:

    4. \begin{array}{ccc} Interval & Test Value & (x+2)^2(x-1)(x-4)\\ \hline (-\infty, -2) & -3 & (+)(-)(-) = (+)\\ ((-2,1) & 0 & (+)(-)(-) =(+)\\ (1,4) & 2 & (+)(+)(-) = (-)\\ (4, \infty) & 5 & (+)(+)(+) = (+)\\ \hline \end{array}

  4. Step 4: Sign chart shows the inequality is true for the interval $(1,4)$. As this is a strict inequality, we exclude the critical points that are the boundary points of this interval, and write the solution set as $x \in (1,4)$

Some inequalities are true for all real numbers. In such cases, we write the answer as "no solution."

Example 4:

Find the solution set of the inequality $(x+2)^2(x^2+5) \leq 0$.

Solution:Note that this inequality has only one critical point $x=-2$. Following table to sign chart shows that the expression is positive for all real number values. \begin{array}{ccc} Interval & Test-Value & (x+2)^2(x^2+5)\\ \hline (-\infty,-2) & -3 & (+)(+)= (+)\\ (-2, \infty) & 0 & (+)(+) = (+)\\ \hline \end{array}

So, the answer to this inequality is "No Solution."

Other than "no Solution", some inequalities can also have unusual solution sets. These sets include "all real numbers", "a single number", and "all real numbers except a single number". Some examples are shown below:

Example 5:

Find solution sets of the inequalities:

$(i)$ $(x+1)^2(x^2-x+1) \gt 0$

$(ii)$ $(x-2)^2(x^2+2x-2) \geq 0$

$(iii)$ $(x-5)^2(x^2+5) \leq 0$

Solution:

$(i)$ $x = -1 $ is the only critical point for this inequality. Sign chart would show that this inequality is positive for all real numbers except $x = -1$. So, the solution set is $(-\infty, -1) \cup (-1, \infty)$

$(ii)$ The only critical point for this inequality is $x = 2$. The polynomial on the right side is positive for all real numbers and equal to zero for $x = 2$. So, the solution set is $(-\infty, \infty)$.

$(iii)$ Critical point for this inequality is $x = 5$. The right side polynomial is positive for all values except $x = 5$. So, the solution set is the single number $x = 5$.

To solve a rational inequality, we find the zeros of both numerator and denominator polynomials and create a sign chart to determine the intervals where the inequality is positive or negative. Critical points for the inequality includes points where the rational expression is zero (zeros of numerator) and the points where the rational expression is undefined (zeros of the denominator).

Example 6:

Determine the solution set of $\frac{(x-2)}{(x+1)(x-3)} \gt 0$

Solution:

Let the rational expression on the right side be represented by $R(x)$.

$R(x)=0$ at $x = 2$ and $R(x)$ is undefined at $x=-1$ and $x=3$.

Draw a sign chart of the number line showing the critical points and the intervals partitioned on the number line by these critical points. 2-7E6

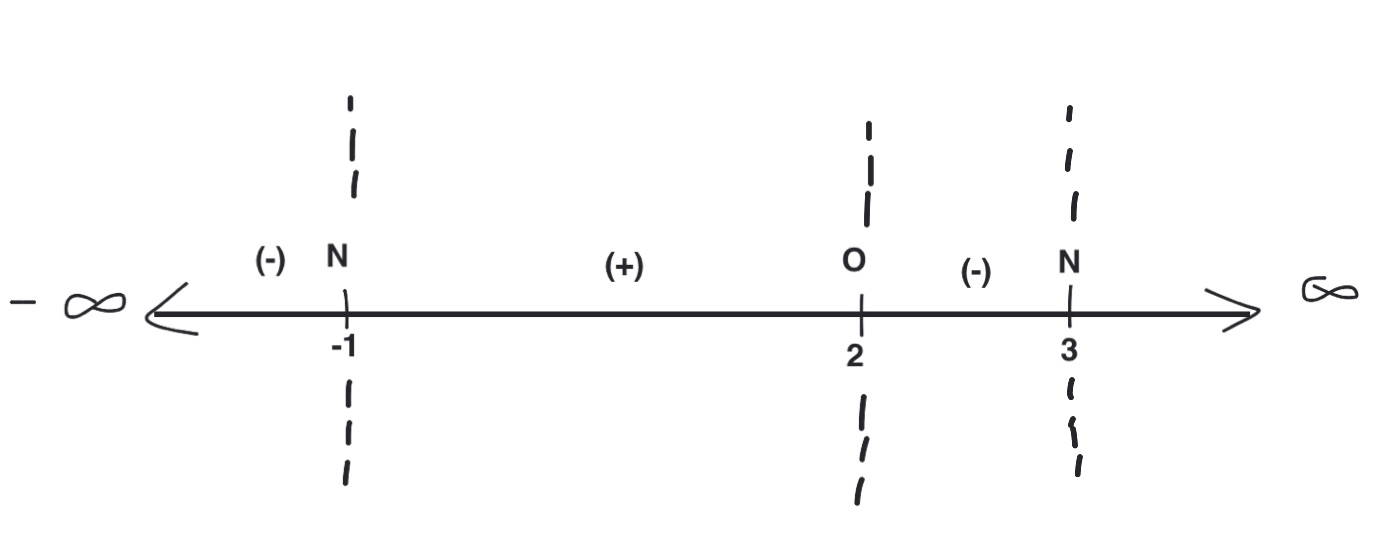
The above sign chart shows that $R(x)$ is positive in the intervals $(-1,2)$ and $(3, \infty)$. As this is a strict inequality, the real zero is not included in the solution set. Hence, the solution set is $(-1, 2) \cup (3, \infty)$.

Example 7:

Find the solution set of $\frac{3}{x+1} - \frac{2}{x-2} \geq 0$

Solution:

First write the left side expression as a single fraction: \begin{eqnarray} \frac{3}{x+1} - \frac{2}{x-2} &\geq& 0\\ \frac{3(x-2)-2(x+1)}{(x+1)(x-2)} &\geq& 0\\ \frac{x-8}{(x+1)(x-2)} &\geq& 0\\ \end{eqnarray}

Real zeros of the right side expression $R(x)$ is $x = 8$ and it is undefined at $x = -1$ and $x = 2$.

Sign chart can be determined using the following table: \begin{array}{ccc} Interval & Test-Value & \frac{x-8}{(x+1((x-2)}\\ \hline (-\infty, -1) & -2 & \frac{(-)}{(-)(-)} = (-)\\ (-1, 2) & 0 & \frac{(-)}{(+)(-)} = (+)\\ (2, 8) & 3 & \frac{(-)}{(+)(+)} = (-)\\ (8, \infty) & 9 & \frac{(+)}{(+)(+)} = (+)\\ \hline \end{array}

So the solution set is $ (-1, 2) \cup [8, \infty)$

Example 8:

Solve the inequality $\frac{x^3-x}{x^2-4} \leq 0$

Solution:

Rewriting the LHS in factor form: $$ \frac{x^3-x}{x^2-4} = \frac{x(x-1)(x+1)}{(x+2)(x-2)}$$. Zeros of LHS are $x = -1, 0, 1$ and undefined points are $x=-2, 2$. Sign chart is shown in the following table:

\begin{array}{ccc} Interval & Test-Value & LHS\\ \hline (-\infty,-2) & -3 & (-)\\ (-2, -1) & -0.5 & (+)\\ (-1, 0) & -0.5 & (-) \\ (0,1) & 0.5 & (+)\\ (1, 2) & 1.5 & (-)\\ (2, \infty) & 3 & (+)\\ \hline \end{array}

As this is an inclusive inequality, the zeros of LHS are included in the solution set. Hence the solution set is $(-\infty,-2) \cup [-1, 0] \cup [1, 2)$

Generally, any algebraic inequality can be solved using the zeros and the undefined points as critical points, partitioning the number line into intervals divided by the critical points, and preparing a sign chart. We need to remember the solution processes and domain restrictions for radical and absolute value equations while solving inequalities involving these expressions.

Practice Problems

$\{\pm1, \pm\frac{1}{2}, \pm 3, \pm\frac{3}{2}\}$; $\{-1, \frac{1+\sqrt{13}}{2}, \frac{1-\sqrt{13}}{2}\}$.

$\{\pm1, \pm \frac{1}{3} \}$; factor form: $(x+1)(-3x^3+x-1)$

$(a)$ Zeros: $x = \{1, \frac{3}{2}, 2\}$;

$(b)$ $P(x) \gt 0$ at $(-\infty, 1) \cup (1, \frac{3}{2}) \cup (2, \infty)$;

$(c)$ $P(x) \lt 0$ at $(\frac{3}{2}, \infty)$.

$(a)$ Zeros: $x = \{-2, 5, 7\}$;

$(b)$ $P(x) \gt 0$ at $(-\infty,-2)\cup (7, \infty)$;

$(c)$ $P(x) \lt 0$ at $(-2, 5) \cup (5,7)$

For problems # 5 - 12, solve each of the following inequalities and write your solution set in interval form:

$[-2, \frac{1}{2}]$

$(1,\infty)$

$[-2,\frac{1}{2}] \cup [3, \infty)$

$(-1, 1) \cup (4, \infty)$

$(\frac{3}{2},\infty)$

$[-1,1]$

$(-\infty,-\frac{1}{2}] \cup [0,3]$

$(\frac{3}{2}, 2)$

$\frac{x^2-5x-3}{(x+1)(x-2)}$

$x=2$

$x = \{-5,2\}$

$(2, \infty)$

$[5,\infty)$

$[-1,0]$

$(-\infty,-5] \cup [-2, \infty)$

$(-\infty, -4) \cup (-\frac{1}{3}, \infty)$

$(-1,\infty)$

$(-3, -\frac{1}{3}] \cup [2, 3)$

$(-2, 2)$

$(-3, 0) \cup (0, 4) \cup (5, \infty)$

$[-2.67,-1) \cup (1,2] \cup [3.77, \infty)$