Precalculus

A rational function is a function of the form $f(x) = \frac{p(c)}{q(c)}$, where $p(x)$ and $q(x)$ are polynomial functions, with $q(x) \neq 0$. This means that the domain of a rational function is the set of all real numbers except those numbers that would make the denominator zero.

Example 1:

Find the domain of the function $f(x) = \frac{2x}{x+2}$

Solution:First we find the zeros of the denominator and then we exclude these real numbers from the domain of $f(x)$. \begin{eqnarray} x + 2 &=& = 0\\ x &=& -2\\ \end{eqnarray}
So, the domain of $f(x)$ is all real numbers except $-2$. We can write this in set notation as $\{x/x \in \mathcal{R}, x \neq -2\}$ and in interval notation as $(-\infty,-2) \cup (-2, \infty)$,

Example 2:

Find the domain of the function $f(x) = \frac{x^2-3x+2}{x^2-9}$

Solution:Setting the denominator to zero, we get the zeros of the denominators as $\{-3,3\}$. So, the domain of $f(x)$ is $\{x / x \in \mathcal{R}, x \neq \pm3\}$ in set notation, and $(-\infty, -3) \cup (-3,3) \cup (3, \infty)$ in interval notation.

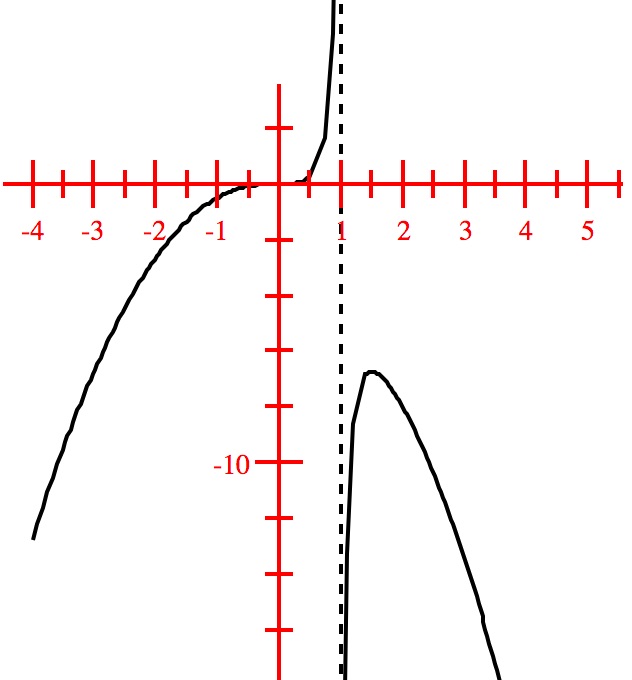
Consider the function $f(x) = \frac{2}{x+2}$. The graph of this function is shown below:

We observe that the graph goes down towards $-\infty$ as $x$ value approaches $-2$ from the left, and it moves up towards $\infty$ as the $x$ valu approaches $-2$ from the right. The graph does not cross the line $x = -2$. Such lines are called Vertical Asymptotes of the graph.
Following steps are used to determine the vertical asymptotes of the graph of a function:

Whenever we cancel the common factors to reduce the function, we have situation where a certain $x$ values are in not in the domain, and this value does not make the denominator zero. So, there is no vertical asymptote at this point. This means that there is a hole on the curve at this point.

Example 3:

Find the vertical asymptote(s) of the graph of the function $f(x) = \frac{x^2-x}{x^2-x+2}$

Solution:Writing the rational expression in factor form, we get $f(x) = \frac{x(x-1)}{(x+1)(x-2)}$.
The zeros of the denominator are $\{1,2\}$. These values are obviously excluded from the domain of this function. The vertical asymptotes are $x=1$ and $x=2$. As there are no common factors, the function is in irreducible. So, there are no holes. The graph of the function is shown below: 2-5E3

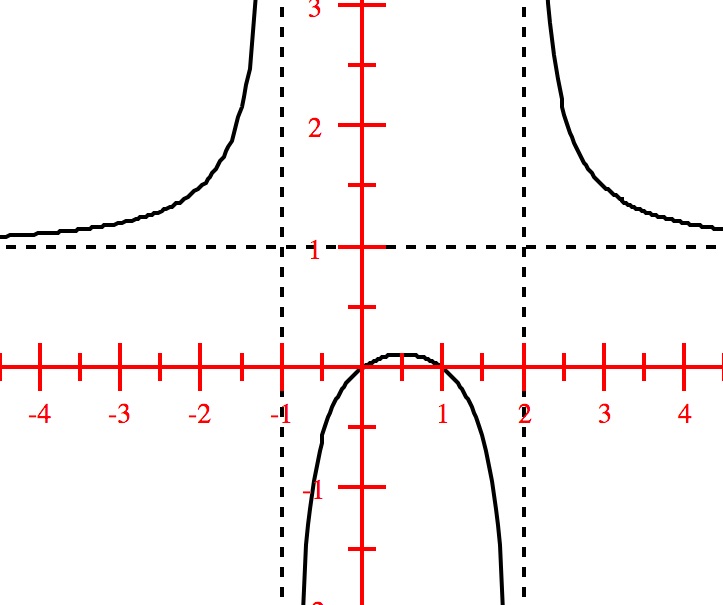
We also note from the graph shown above that, as the graph tends to approach the line $y=1$,the $x \rightarrow -\infty$ on the left and $x \rightarrow \infty$ on the right. The graph does not cross the line $y=1$ anywhere in its domain. Such lines are called Horizontal Asymptotes..
The following criteria are usually used to determine the horizontal asymptotes:
Consider the rational function $f(x) = \frac{p(x)}{q(x)}$, where the degree of $p(x) = a_{m}x^m + a_{m-1} x^{m-} + \ldots $ is $m$, and the degree of $q(x)=b_{n}x^n + b_{n-1}x^{n-1} \ldots $ is $n$. Then,

If $m \gt n$, we can divide $p(x)$ by $q(x)$, so that we get the summary statement as $f(x) = Q(x) + \frac{R(x)}{q(x)}$, where, $Q(x)$ and $R(x)$ are the quotient and the remainder of the division respectively. In this case, there will ba slant asymptote for the graph at $y = Q(x)$. The slant asymptote is not always a straight line. It depends on the quotient polynomial of the division. Hence, this asymptote is also referred to as the 'end-behavior asymptote.'
To sketch the graph of a rational function, we need to first determine the following characteristics of the graph:

Example 4:

Find the asymptotes of the function $f(x) = \frac{-4}{x+2}$.

Solution:$(i)$ Vertical asymptote is determined by finding the zeros of the denominator: \begin{eqnarray} x+2 &=& 0\\ x &=& -2\\ \end{eqnarray} So, vertical asymptote is $x=-2$. Also, as the function in irreducible, there are no holes in the graph.
$(ii)$ The degree of the numerator is $0$ and the degree of the denominator is $1$. So, the horizontal asymptote is $y = 0$.
$(iii)$ The degree of numerator is less than the degree of denominator.So, no slant asymptote.

Example 5:

Determine the asymptotes of the function $f(x) = \frac{4x-3}{x-1}$

Solution:$(i)$ Vertical asymptote is $x = 1$. There are no holes.
$(ii)$ Degree of numerator is equal to the degree of the denominator. So, the horizontal asymptote is $y = \frac{4}{1}$, which is $y=4$.
$(iii)$ As the degrees of the numerator and denominator are equal, there is no slant asymptote.

Example 6:

Find the equations of the asymptotes of the function $f(x) = \frac{x^2-4x+3}{x+4}$

Solution:$(i)$ Vertical asymptote is $x = -4$. There are no holes.
$(ii)$ No horizontal asymptote.
$(iii)$ Degree of numerator is greater than the degree of the denominator. Dviding the numerator by the denominator results in the summary statement $\frac{x^2-4x+3}{x+4} = x(x-4) + 3$. So, slant asymptote is $y = x$.

Following points are to be analyzed before sketching the graph of a rational function:

Example 7:

Find the intercepts, asymptotes, and domain of the function $f(x) = \frac{x-1}{x^2-3x+2}$ and sketch a graph of the function. Include additional points, as may be necessary.

Solution:Reducing the fraction to lowest terms, we get $f(x) = \frac{1}{x-2}$.
$x$- intercept: Setting $x=0$, we get $y = f(x) = \frac{1}{-2}$. So, $x$- intercept: none. Setting $y=0$ in the original function gives $x=1$, but this is not in the domain of the function; $y$- intercept: Setting $x=0$ in the function gives $y=-\frac{1}{2}$. So, $y$- intercept is $(0,-\frac{1}{2})$.
Vertical asymptote:Setting the denominator to zero in the reduced function gives $x=2$. So, vertical asymptote is $x=2$; horizontal asymptote: As the degree of the numerator is less than the degree of the denominator, horizontal asymptote is $y = 0$;
Domain: $\{x| x \in \mathcal{R}; x \neq 1 \quad or \quad 2 \}$.
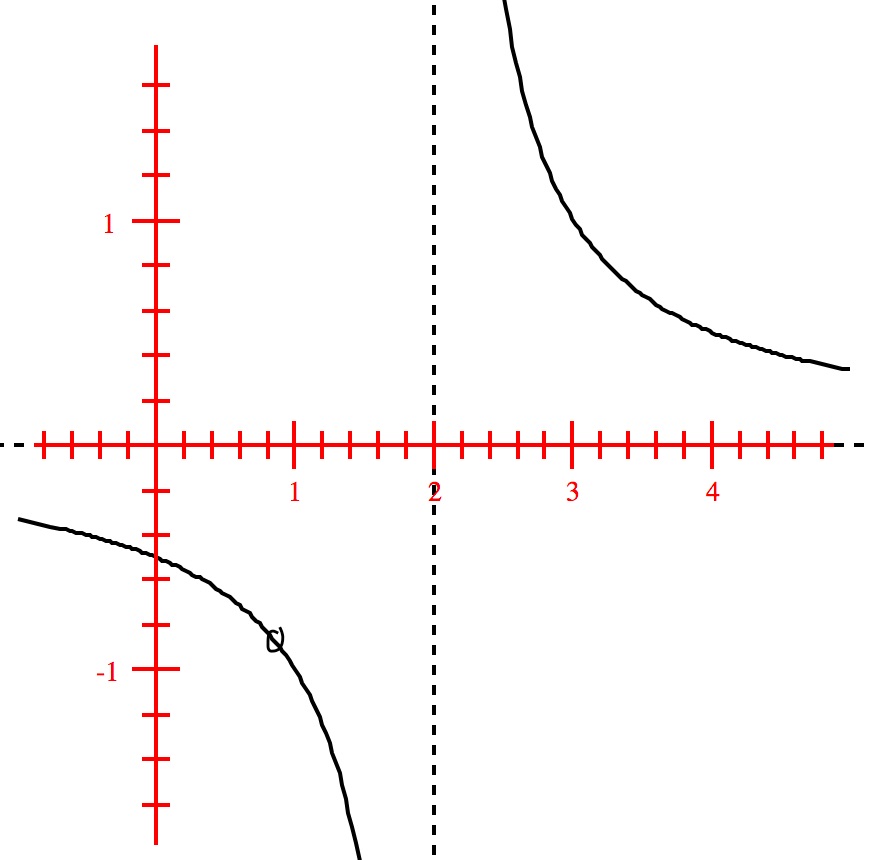
Note that we canceled the common factor $(x-1)$ in order to reduce the function. This means that $x=1$ is not in the domain,neither is there a vertical asymptote at $x=1$. Hence the graph has a hole at the point $(1, f(1))$. i.e., $(1, -1)$Graph is shown below. 2-5E7

Example 8:

Find the asymptotes and intercepts of the rational function $f(x)=\frac{3x^2-x-4}{x^2-4}$

Solution:$(i)$ Asymptotes: We note that $f(x)$ cannot be reduced further as there are no common factors. So, equation of vertical asymptote is got be setting the denominator to zero. We get two vertical asymptotes, whose equation are $x = 2$ and $x = -2$;, and no holes.
We note that the degrees of the numerator and denominator are equal, both being of second degree. So, the equation of the horizontal asymptote is $y = \frac{3}{1}$, which is $y = 3$.
$(ii)$ Intercepts: $x$-intercept is got by setting the numerator of the function to zero and solving for $x$. \begin{eqnarray} 3x^2-x-4 &=& 0\\ (x+1)(3x-4) &=& 0\\ x=-1, x=\frac{4}{3}\\ \end{eqnarray}
So, $x$-intercepts are $(-1.0)$ and $(\frac{4}{3},0)$; $y$- intercept is obtained by setting $x=0$ and evaluating the function: \begin{eqnarray} f(x) &=& \frac{3x^2-x-4}{x^2-4}\\ f(0) &=& \frac{-4}{4}\\ f(0) &=& -1\\ \end{eqnarray}.
So, the $y$- intercept is $(0,-1)$.

Example 9:

Determine the intercepts, asymptotes, and end-behavior asymptotes for the function $f(x) = \frac{x^2-9}{x+1}$

Solution:Intercepts: $x$- intercepts are got by setting the numerator to zero: $(3,0)$ and $(-3,0)$; $y$- intercepts are got by setting $x=0$ and evaluating the function: $(0,-9)$.
Asymptotes: As the function cannot be reduced further, equation of the vertical asymptote is obtained by setting the denominator to zero: $x = -1$; As the degree of the numerator $(2)$ is more than the degree of the denominator $(1)$, graph of this function does not have a horizontal asymptote. Ene-behavior asymptote is obtained by finding the quotient polynomial of the division, which is $x-1$. This is a linear polynomial. So, the end-behavior is a straight line with equation $y - x-1$.

Example 10:

Determine the intercepts, asymptotes, and end-behavior asymptotes for the function $f(x) = \frac{x^3-2x^2+x-2}{x-1}$.

Solution:Intercepts: $x$- intercept is got by setting the numerator to zero. \begin{eqnarray} x^3-2x^2+x-2 &=& 0\\ x^2(x-2)+1(x-2) &=& 0\\ (x^2+1)(x-2) &=& 0\\ \end{eqnarray}.
As $x^2+1=1$ does not result in any real value for $x$, there is only one $x$- intercept $(2,0)$.
$y$- intercept is obtained by evaluating $f(0)$, which gives the $y$- intercept $(0, 2)$.
The function is in irreducible form. So, equation of the verticalasymptote is $x=1$.
Degree of numerator is greater than degree of denominator.So, there is no horizontal asymptote.
Dividing the numerator by the denominator gives the quotient polynomial $Q(x) = x^2-x$. So,the end-behavior asymptote is $y=x^2-x$,which is a parabola. Graph of this function is shown below, with all the asymptotes.

Practice Problems

Domain: All real numbers $x$, such that $x \neq -3$.

Domain: $(-\infty, -4) \cup (-4,4) \cup (4, \infty)$

$x=3$ and $x=-3$

$x=2$

No vertical asymptotes

$x=3$

$y=0$

$y=\frac{1}{2}$

No horizontal asymptote.

None.

$y=x-5$

$y=x^2-3x+5$

Vertical asymptotes: $x=0$ and $x=2$; Horizontal asymptote: $y=0$;

No vertical asymptote; horizontal asymptote: $y = -1$

Vertical asymptote: $x=-3$; horizontal asymptote: None: slant asymptote: $y=3x+7$

$(0,0)$

$(0,0)$, $(2,0)$, and $(-2,0)$

$(0,-3)$

$x$- intercepts: $(2,0)$ and $(-2,0)$; $y$- intercept: $(0,-2)$

Vertical asymptote: $x=3$ and $x=-1$; horizontal asymptote: $y=0$; $x$-intercept: $(1,0)$; $y$- intercept: $(0, \frac{1}{3})$.

Vertical asymptote: $x=5$; horizontal asymptote: $y=3$; $x$-intercept: $(-1,0)$ and $(\frac{4}{3})$; $y$-intercept: $(0,\frac{4}{5})$.

Vertical asymptote: $x=-2$; Horizontal asymptote: None; Slant asymptote: $y=x$; $x$-intercept: $(-3,0)$ and $(1,0)$; $y$-intercept: $(0,-\frac{3}{2})$.

Vertical asymptote: $x=2$; end-behavior asymptote: $y=x^2+x+1$; horizontal asymptote: none; $x$-intercept: $(1-1,0)$, $(1,0)$, which has multiplicity 2. So, the graph crosses the $x$-axis at $x=-1$ and touches it at $x=1$; $y$-intercept: $(0, -\frac{1}{2})$. Graph is shown below.

Vertical asymptotes: $x=-3$ and $x=2$; Horizontal asymptote: $y=0$; $x$-intercepts: $(3,0)$; $y$-intercept: $(0,1)$.

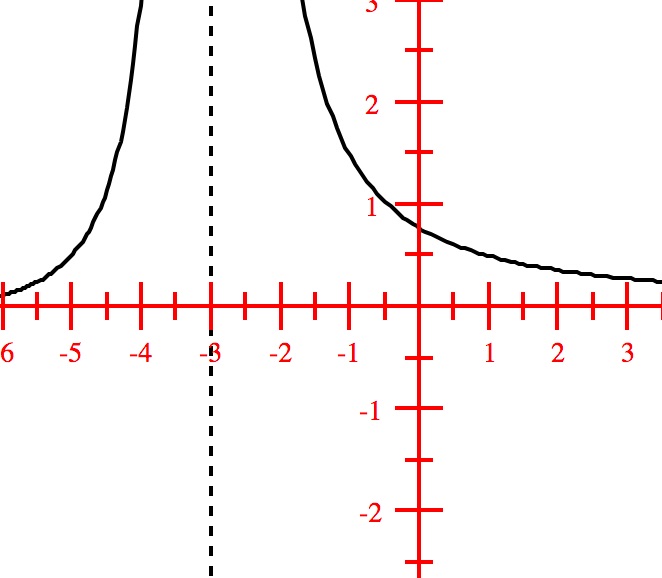
Domain: $(-\infty, -3) \cup (-3, \infty)$; Vertical asymptote: $x=-3$; No holes in the graph; Horizontal asymptote: $y=0$; $x$-intercepts: $(-7,0)$; $y$-intercept: $(0,1)$

Domain: $(-\infty, -1)\cup(-1,1)\cup(1,\infty)$; Vertical asymptote: $x=1$; Hole at the point $(-1, -\frac{3}{2}$; Slant asymptote: $y=x$ No $x$-intercepts; $y$-intercept: $(0,-1)$

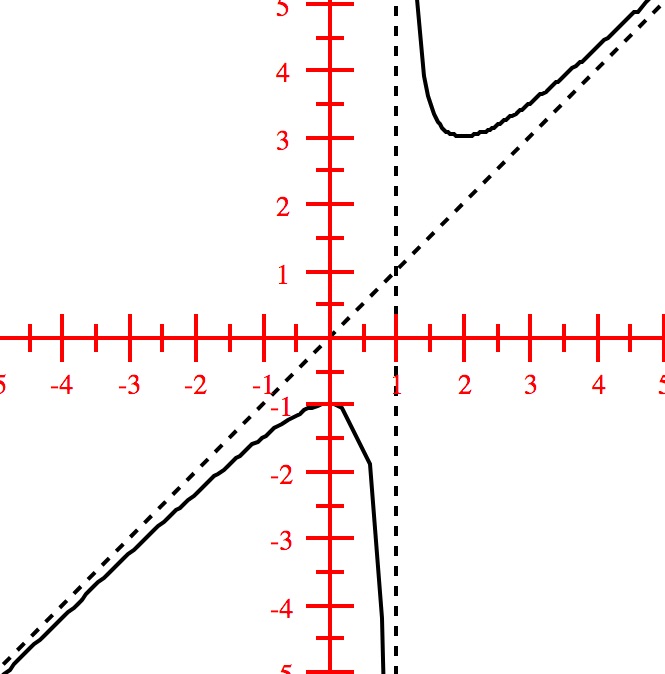
Domain: $(-\infty, \infty)$; Vertical asymptote: $x=2$; Hole at $(-3, \frac{7}{5})$; Horizontal asymptote: $y=1$;

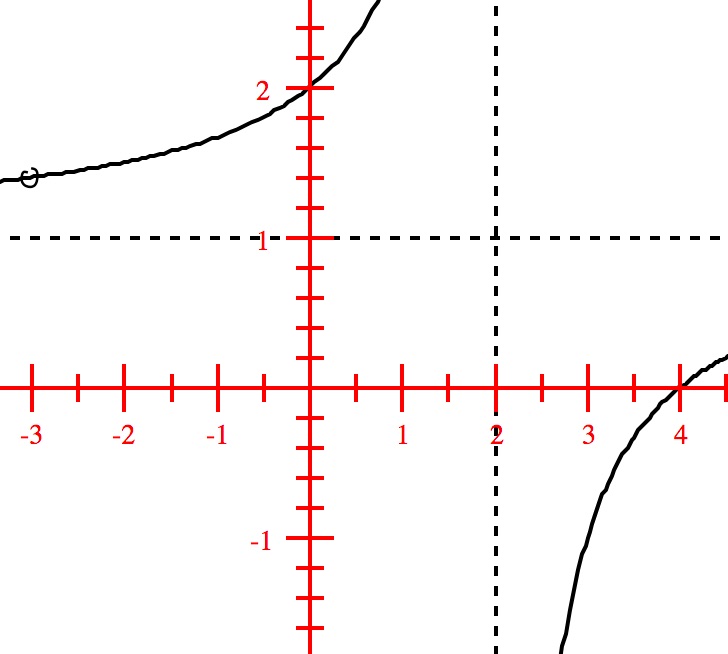
Domain: $(-\infty, 1) \cup (1,\infty)$; Vertical asymptote: $x=1$; No horizontal or slant asymptote; No holes in the graph; $x$-intercept and $y$-intercept: $(0,0)$. Graph shown below: