Precalculus

A polynomial function is a collection of one or more monomial functions, related by the operation of addition or subtraction. It can be written in the form $f(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} +.........+a_3x^3 + a_2x^2 + a_1x + a_0$, where $a_n, a_{n-1}, .... a_2, a_1, a_0$ are real numbers with $a_n \neq 0$. Each monomial of this function is call a term of the polynomial. When the polynomial is written in descending order of degree of the terms as above, this form is referred to as the standard form .

The first and the highest degree term is called the leading term and the coefficient of the leading term is called the leading coefficient of the polynomial. The last term of a polynomial $a_0$, if it exists, is called the constant term. This is a monomial of degree $0$. A polynomial function has all real numbers as its domain.

Example 1:

Rewrite the following polynomial functions in the standard form and find the degree, leading term, leading coefficient, and the constant term:
$(i) \quad f(x)=2x-3x^3+4x^2-5$
$(ii) \quad f(x)=5x-12x^6$
$(iii) \quad f(x)=2x^4+7x^5-3-5x^2+12x$
$(iv)\quad g(t) = \frac{2t-t^3+7t^5}{5t}$

Solution: $(i)$ Standard form: $f(x)=-3x^3+4x^2+2x-5$; Degree: $3$; Leading term: $-3x^3$; Leading coefficient: $-3$.
$(ii)$ Standard form: $f(x)=-12x^6+5x$; Degree: $6$; Leading term: $-12x^6$; Leading coefficient: $-12$.
$(iii)$ Standard form: $f(x)=7x^5+2x^4-5x^2+12x-3$; Degree: $5$; Leading term: $7x^5$; Leading coefficient: $7$.
$(iv)$ Rewriting this function in standard form: \begin{eqnarray} g(t)) &=& \frac{2t}{5t} - \frac{t^3}{5t}+ \frac{7t^5}{5t}\\ &=& \frac{2}{5}-\frac{t^2}{5}+\frac{7t^4}{5}\\ &=& \frac{7}{5}t^4 -\frac{1}{5}t^2+\frac{2}{5}\\ \end{eqnarray}
Degree: $4$; Leading term: $\frac{7}{5}t^4$; Leading coefficient: $\frac{7}{5}$.

To graph a polynomial we shall determine the following aspects of the graph of the functions:

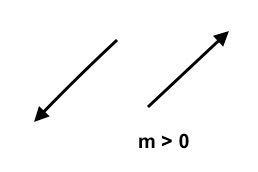
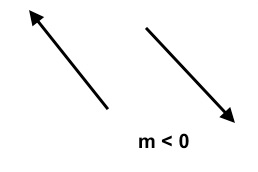
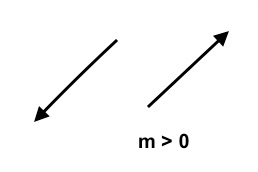
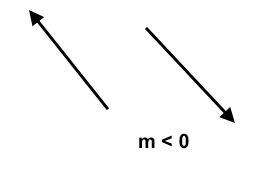
End behavior of polynomial functions are similar to the end behavior of the respective leading terms. For example, we already know that, for a linear monomial $y=mx$ goes up (rises) when $m$ is positive and goes down (falls) if $m$ is negative. In more mathematical terms, we can say that, if $m \gt 0$, then, as $x \rightarrow -\infty, \quad y \rightarrow -\infty$ and as $x \rightarrow \infty, \quad y \rightarrow \infty$, and, if t $m \lt 0$, then, as $x \rightarrow -\infty \quad y \rightarrow \infty$ and as $x \rightarrow \infty, \quad y \rightarrow -\infty$.

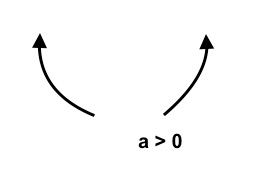
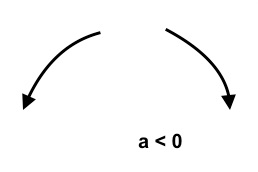
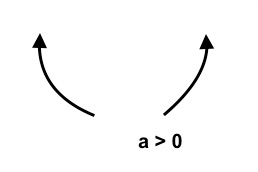
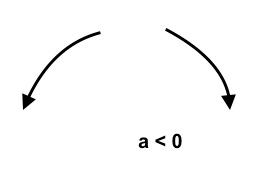
A quadratic polynomial function $f(x)=ax^2$ with positive leading coefficient goes up at both ends, and, if the leading coefficient is negative, it goes down at both ends. This would mean that the $U$ shape of the graph of the polynomial function opens up if the leading coefficient is positive and it opens down if the leading coefficient is negative. Mathematically, we can write this as "If $a \gt 0$, as $x \rightarrow -\infty, \quad y \rightarrow \infty$ and as $x \rightarrow \infty, \quad y \rightarrow \infty$. If $a \lt 0$, as $x \rightarrow -\infty, \quad y \rightarrow -\infty$ and as $x \rightarrow \infty, \quad y \rightarrow -\infty$."

Example 2:

Determine the end behavior of the following functions:
$(i) f(x)=3x^2-2x+1; \quad (ii) f(x) = -x^2-x+2, \quad (iii) y=3x-1, \quad h(t)=-t+5$

Solution:$(i)$ This is a quadratic polynomial with leading coefficient $3$, which is positive. So, the graph goes up at both ends, and has the shape of $U$, opening up. That is, as $x \rightarrow -\infty, \quad y \rightarrow \infty$ and as $x \rightarrow \infty, y \rightarrow \infty$

$(ii)$ This is a quadratic polynomial with negative leading coefficient. So,the graph opens down. It goes down at both ends. That is, as $x \rightarrow -\infty, \quad y \rightarrow -\infty$ and as $x \rightarrow \infty, \quad y \rightarrow -\infty$.

$(iii)$. This is a monomial with positive leading coefficient. So, the graph is a rising line. That is, as $x \rightarrow -\infty,\quad y \rightarrow -\infty$ and as $x \rightarrow \infty, \quad y \rightarrow \infty$.

$(iv)$. This is a monomial with negative leading coefficient. So,the graph is a falling line. That is, as $x \rightarrow -\infty, \quad y \rightarrow \infty$ and as $x \rightarrow \infty, \quad y \rightarrow -\infty$. Figure 2-3E2iv

Generally, all polynomial functions of even degree have the same end behavior. Similarly, all odd degree polynomials have similar end behavior. But the number of turning points , which are also called the local extremas, depends on the degree of the polynomial. So, it is useful to identify the left-end and right-end behavior of the graph of a polynomial function separately, and fill the gap using the number of turning points and intercepts, etc.

Example 3:

Determine the end behavior of the graph of the following polynomials:

$(i) f(x)=x^3-2x^2+6; \quad$

(ii) $f(x) = -2x^6+3x^3+7x^2-5$;

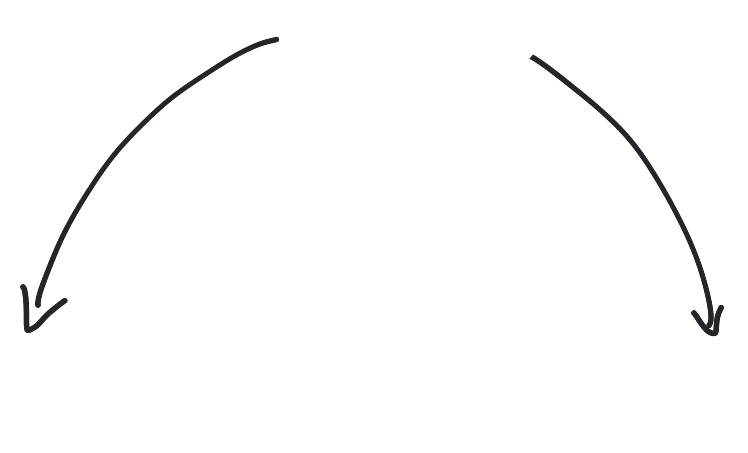
Solution: $(i)$ Leading term of this polynomial is$x^3$. So, the end behavior would be similar to the monomial of odd degree with positive coefficient. That is, as $x \rightarrow -\infty, \quad y \rightarrow -\infty$ and as $x \rightarrow \infty, \quad y \rightarrow \infty$.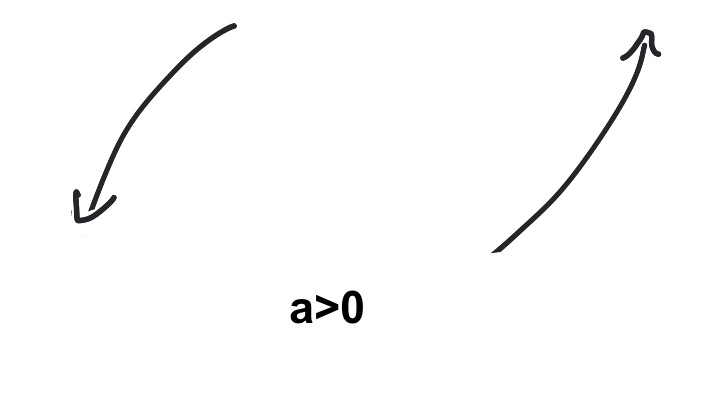
2-3E3i

$(ii)$ Leading term is $-2x^6$, which has degree 6 and coefficient $-2$. So, as $x \rightarrow -\infty, \quad y \rightarrow \infty$ and as $x \rightarrow \infty, \quad y \rightarrow, -\infty$.

2-3E3ii

Example 4:

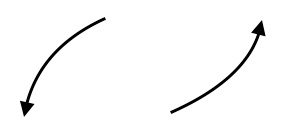
Determine the end behavior of each of the following polynomial functions:
$(i) 2x^5-3x^4+x^2=10; \quad (ii) f(x)=-5x^7+7x^4+11;$
$ (iii) f(x)= 8x^4-2x^3-x^2+6; \quad (iv) f(x)=-4x^8-x^7+2x^4-7x^2+x$

Solution: $(i)$ Odd degree with positive leading coefficient. So, end behavior of similar to that of linear polynomial with positive leading coefficient.

$(ii)$ Odd degree with negative coefficient. So, end behavior is similar to that of linear polynomial with leading negative coefficient.

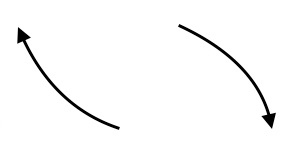
$(iii)$ Even degree with positive leading coefficient. So, the end behavior is similar to that of quadratic polynomial with positive leading coefficient.

$(iv)$ Even degree with negative coefficient. So, the end behavior is similar to that of quadratic polynomial with negative coefficient.

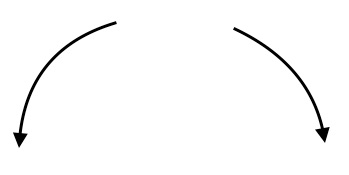
From the above discussions and examples, we infer a general rule for determining the end behavior of polynomial functions:
For any polynomial function $f(x)$ with leading term $a_nx^n$,

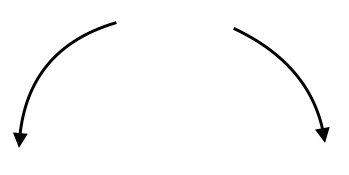
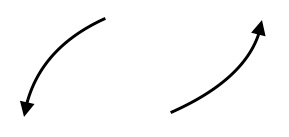
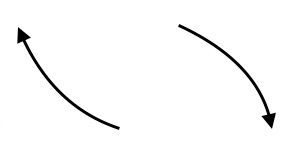
Number of turning points in the graph of a function is the point in which the graph changes direction. For polynomial function of degree $n$, the graph has at most $n-1$ turning points. The graph of a linear function does not change in direction.. It has $0$ turning points. Graph of a quadratic equation has one turning point. Graphs of cubic and quartic polynomials have $2$ and $3$ turning points respectively.

$y$- intercept of a function is obtained by setting $x = 0$ in the equation and solving it for $y$, because all points on the $y$- axis have $x$- coordinates $0$. This is the point where the graph intersects the $y$-axis.

Example 5:

Find the $y$- intercept of the function $f(x) = x^3-6x^2+x-5$

Solution: Setting $x = 0$ in the equation, we get $f(x)=-5$. So, the $y$- intercept is $-5$. This means that the graph of this function intersects the $y$- axis at the point $(0, -5)$.

$x$- intercepts of a function is obtained by setting setting $y=0$ in the equation and solving it for $x$, because all points on the $x$-axis have $y$-coordinates $0$. Graph of a function may intersect the $x$-axis at one of more points. The solutions of the equation when we set $y=f(x)=0$ are also called the roots or zeros of the functions.
In general, a polynomial function of degree $n$ has at most $n$ zeros. Of these $n$ zeros, the ones with even multiplicity do not cross the $x$-axis, but touch it from above or below. The zeros of odd multiplicity cross the $x$- axis, from above to below or from below to above the $x$-axis. The graphs shown below explain this concept clearly.

Example 6:

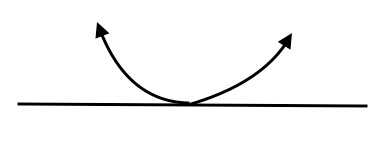
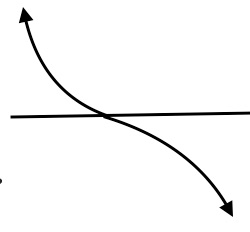
Find the $x$- intercepts of the polynomial functions $(i) f(x)=x^3-2x^2+x; \quad (ii) f(x)=(x-1)(x+2)^2(x+4)^3$

Solution: $(i)$ Setting $y=0$ and solving for $x$, we get \begin{eqnarray} x^3-2x^2+x &=& 0\\ x(x^2-2x+1) &=& 0\\ x(x-1)^2 &=& 0\\ x &=& 0, 1,1\\ \end{eqnarray} $x=0$ is a zero of multiplicity 1 and so the graph crosses the $x$-axis at this point. $x=1$ is a zero of multiplicity 2 and so the graph touches the $x$-axis at this point.
$(ii)$ Setting $y=0$ in the above equation results in the equation $(x-1)(x+2)^2(x+4)^3=0$ Using the zero-product rule, we get the solution set $x={1,-2,-2,-4,-4,-4}$. We see that $x=1$is a zero of multiplicity $1$, $x=-2$ is a zero of multiplicity $2$, and $x=-4$ is a zero of multiplicity 3. So, the graph touches the $x$ - axis at the point $(-2,0)$, and croos the $x$- axis at $(1,0)$ and $(-4,0)$. We may need to find some additional points on graph to get more detail about the graph.

Symmetry of the graph of a function, if it exists, can be determined by finding whether the function is even or odd. As we have already discussed in Chapter 1, odd functionS are symmetric about the origin and even functions are symmetric about the $y$- axis. A function that is neither even nor odd does not have any of these symmetries, although it may have some other symmetry.

Additional points on the graph of a function are obtained by considering one point in each interval caused by the zeros of the function, and evaluating the function to get the $y$-coordinates of these points.

Example 7:

Analyze the function $f(x)=x^4-x^3-12x^2$ and determine the end behavior, number of turning points, intercepts, symmetry. Sketch the function by finding some additional points if needed.

Solution: This is an even degree polynomial function with positive leading coefficient. So, the end behavior is similar to that of a quadratic function with positive leading coefficient.
2-3Li
The degree is $4$. So, the graph has at most 3 turning points.
To find $y$-intercept, setting $x=0$, we get $y=0$.
To get $x$-intercepts, setting $y=0$, we get \begin{eqnarray} x^4-x^3-12x^2 &=& 0\\ x^2(x^2-x-12) &=& 0\\ x^2(x-4)(x+3) &=& 0\\ x &=& 0,\quad 0,\quad 4,\quad -3\\ \end{eqnarray}

Using the multiplicity rule, we infer that the graph touches the $x$-axis at $x=0$ and crosses the $x$-axis at $x=4$ and $x=-3$.
Setting $x=-x$ in the function, we get \begin{eqnarray} f(-x) &=& (-x)^4 - (-x)^3 - 12(-x)^2\\ &=& x^4 + x^3 -12x^2\\ &\neq& f(x)\\ \end{eqnarray} So, the function is neither even nor odd. This means that the graph has none of these two symmetries.
In order to get additional points, we divide the $x$-axis into open intervals using the zeros: $(-\infty,-3), (-3.0)$, and $(0,4)$. We take one $x$ value in each of these four intervals, and find the corresponding $y$ coordinate. As the graph does not cross or touch the $x$-axis in any point other than the zeros, the portions above or below the $x$-axis would remain above or below throughout that interval. Also, any point above the $x$-axis has positive $y$- coordinate and any point below the $x$-axis has negative $y$ coordinate. Using these facts helps us sketch a graph that is fairly close to the actual graph. The following table shows the additional points:
\begin{array}{ccc} x & y & (x,y)\\ \hline -4 & 128 & (-4,128)\\ -1 & -10 & (-1,-10) \\ 1 & -12 & (1,-12) \\ 5 & 200 & (5,200) \\ \hline \end{array}

From the above table, we infer that the graph is above the $x$-axis in the interval $(-\infty,-3)$ crosses the $x$-axis at $x=-3$ and goes below the $x$-axis. Then, it touches the $x$-axis at $x=0$ and turns back to remain below the $x$ axis. Finally, it crosses the $x$-axis at $x=4$ and goes above the $x$-axis again.
A sketch of this polynomial function is shown below.

Example 8:

Analyze the function $f(x)=(x-2)^2(x+1)^2(x-3)$ and determine the end behavior, number of turning points, intercepts, symmetry. Sketch the function by finding some additional points if needed.

Solution: This is an odd degree polynomial function with positive leading coefficient. So, the end behavior is similar to that of a quadratic function with positive leading coefficient.
2-3Liii
The degree is $5$. So, the graph has at most $4$ turning points.
To find $y$-intercept, setting $x=0$: \begin{eqnarray} y &=& (0-2)^2(0+1)^2(0-3)\\&=& (4)(1)(-3)\\ &=& -12\\ \end{eqnarray}
So, the graph intersects the $y$-axis at $(0,-12)$.
To get $x$-intercepts, setting $y=0$, we get \begin{eqnarray}(x-2)^2(x+1)^2(x-3) &=& 0\\ x &=& 2, \quad 2 \quad -1, \quad -1 \quad 3\\ \end{eqnarray}
Using the multiplicity rule, we infer that the graph touches the $x$-axis at $x=2$ and at $x=1$, and crosses the $x$-axis at $x=3$.
For determining symmetry, we first find whether the function is even or odd. Settng $x=-x$ in the function, we get \begin{eqnarray} f(-x) &=& (-x-2)^2(-x+1)^2(-x-3)\\ &=& (x+2)^2(-x+1)^2(-x-3)\\ &\neq& f(x)\\ \end{eqnarray}
So, the function is neither even nor odd. This means that the graph has none of these two symmetries.
In order to get additional points, we divide the $x$-axis into open intervals using the zeros: $(-\infty,-1), (-1.2)$, and $(2,3)$, and $(3, \infty)$. We take one $x$ value in each of these four intervals, and find the corresponding $y$ coordinates. As the graph does not cross or touch the $x$-axis in any point other than the zeros, the portions above or below the $x$-axis would remain above or below throughout that interval. Also, any point above the $x$-axis has positive $y$- coordinate and any point below the $x$-axis has negative $y$ coordinate. Using these facts helps us sketch a graph that is fairly close to the actual graph. The following table shows the additional points:
\begin{array}{ccc} x & y & (x,y)\\ \hline -2 & 96 & (-2,96)\\ 0 & -10 & (0,-16) \\ 2.5 & -4 & (2.5,-4.6) \\ 4 & 54 & (4,25) \\ \hline \end{array}

Example 9:

Find a cubic polynomial having zeros $1, -2, 4$

Solution: Working backwards, assuming the leading coefficient as a multiple of a real number $a$, we get \begin{eqnarray} f(x) &=& a(x-1)(x+2)(x-4)\\ &=& a(x^2-x+2)(x-4)\\ &=& a(x^3-3x^2-6x+8)\\ \end{eqnarray}

For the problems # 1 - 9, find the $(i)$ end behavior, $(ii)$ number of turning points, $(iii)$ $x$- and $y$- intercepts, and $(iv)$ symmetry.

Practice Problems

$(i)$ odd degree with positive leading coefficient: 2.3P1
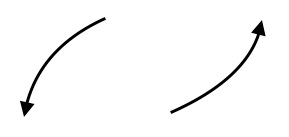$(ii)$ 2 turning points.
$(iii)$ $x$- intercept $(0,0)$ and $y$- intercept $(0,0)$.
$(iv)$ symmetric about origin.

$(i)$ even degree with positive leading coefficient: 2.3P2
$(ii)$ 3 turning points; $(iii)$ $x$- intercepts $(-1,0)$, $(2,0)$, and $(3,0)$ and $y$- intercept $(0, 6)$.
$(iv)$ no symmetry.

$(i)$ odd degree with positive leading coefficient: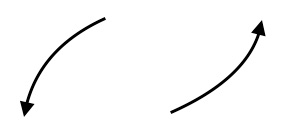 2.3P3
$(ii)$ 4 turning points;
$(iii)$ $x$- intercepts $(-1,0)$ and $(3,0)$; $y$- intercept $(0,27)$;
$(iv)$ no symmetry.

$(i)$ even degree with positive leading coefficient: 2.3P4
$(ii)$ 3 turning points;
$(iii)$ $x$- intercept $(2,0)$ and $(-2,0)$; $y$- intercept $(0,16)$;
$(iv)$ symmetric about $x$-axis.

$(i)$ Odd degree with negative leading coefficient: 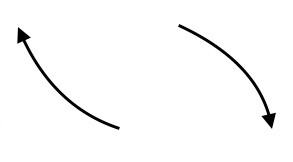2.3P5
$(ii)$ 2 turning points;
$(iii)$ $x$-intercepts $(1,0)$, $(-3,0)$;
$(iv)$ No symmetry.

$(i)$ Even degree with positive coefficient: 2.3P6
$(ii)$ 3 turning points;
$(iii)$ $x$-intercepts: $(1,0)$, $(-2,0)$;
$(iv)$ No symmetry.

$(i)$ Even degree with negative leading coefficient: 2.3P7
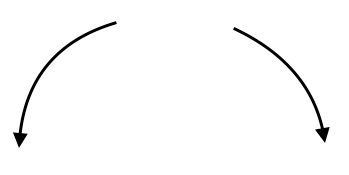$(ii)$ 3 turning points;
$(iii)$ $x$-intercepts: $(0,0)$, $(-4,0)$;
$(iv)$ No symmetry.

$(i)$ Odd degree with positive leading coefficient: 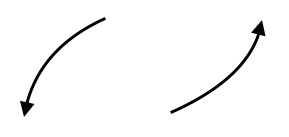2.3P8
$(ii)$ 4 turning points;
$(iii)$ $x$-intercepts: $(0,0)$, $(2,0)$, $(-2,0)$;
$(iv)$ Symmetric about origin.

$(i)$ Even degree with negative leading coefficient: 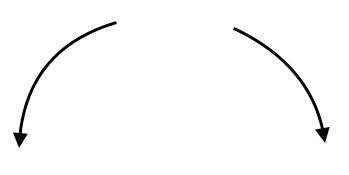2.3P95
$(ii)$ 3 turning points; <
$(iii)$ $x$-intercept: $(\sqrt{3},0)$, $(-\sqrt{3},0)$;
$(iv)$ Symmetric about $y$-axis.

For problems #10-14, sketch a graph of the given function, showing clearly the end behavior, turning points, and zeros. You may use a calculator to graph.

Zeros are $3$ with multiplicity 2 and $-5$ with multiplicity 3. The graph of the function crosses the $x$-axis at $x=-53$ and touches it at $x=3$.

Zero are $0$ with multiplicity 3, $-2$ with multiplicity 1, and $1$ with multiplicity 2. The graph of the function crosses the $x$-axis at $x=0$ and $x=-2$, and touches it at $x=1$.

$f(x)= x^3-5x^2-24x+72$

$x^3-3x^2-2x+6$

$-1, 0, 2$

$(0,5)$

$f(x)=-x(x-2)^2(x+2)$

Zeros are $-3, -1, 1$, with multiplicities 3, 6, and 2 respectively. Graph crosses the $x$- axis at $x=-3$ and touches it at $x=1$ and $x=-1$.