Dr. Lalitha Subramanian
About the Author

Aksharam
A polynomial of degree $0$ is a constant monomial, as this has only one term. Graph of this constant monomial $y = k$ is a horizontal line, $k$ units away from the $x$-axis. A polynomial of degree $1$ is called a linear polynomial function. Standard form of a linear polynomial is $f(x) = mx+b$, which can also be written as $y = mx + b$, $m$ and $b$ are real numbers and $m \neq 0$. As we can see, this is a binomial function. Graph of a linear polynomial function is a slanting line, with slope $m$ and $y$- intercept $b$. The graph is a rising line if $m \gt 0$ and it is a falling line if $m \lt 0$. A polynomial of degree $2$ is called a quadratic polynomial function.Standard form of a quadratic polynomial is $f(x) = ax^2 + bx + c$, where $a$, $b$, and $c$ are real numbers and $a \neq 0$. Graphs of quadratic polynomial functions are "U" shaped. This U shape opens upwards if the coefficient of the $x^2$ term $a$ is positive and opens downwards if $a$ is negative.
We know that two distinct points determine a unique line. So, the slope $m$ can be determined if we know the coordinates of two d distinct points on the line. Formula for finding the slope of a line passing through the points $(x_1,y_1)$ and $(x_2,y_2)$ is $$ m = \frac{y_2 - y_1}{x_2 - x_1}$$.
Find the slope of each of the following lines, plot these points and graph the line joining them. Then identify the $x$ and $y$ intercepts of these lines: $(i) P(0,1), Q(2,3) \quad (ii) A(-1,2), B(3,0) \quad (iii) X(2,3), Y(4,-1) \quad (iv) A(-3,1), B(2,-3)$
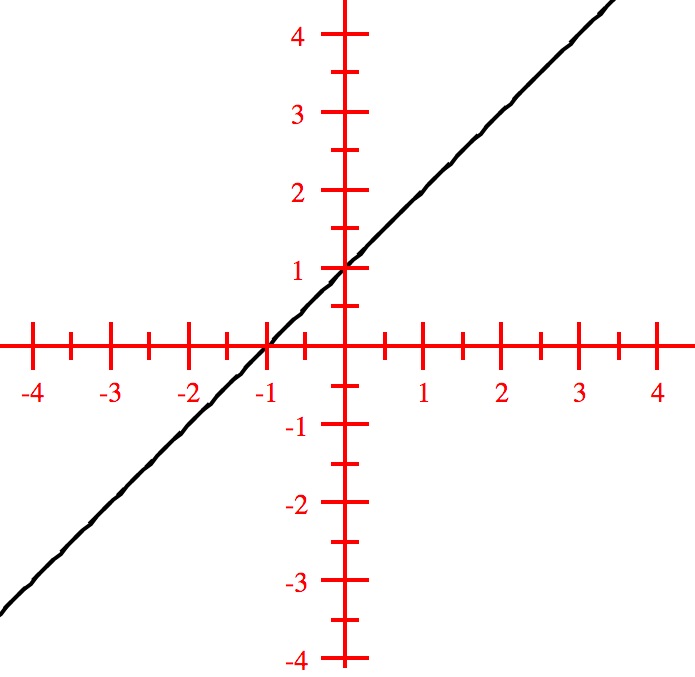
Solution: $(i)$ Slope is $\frac{3-1}{2-0} = \frac{2}{2} = 1$. From the graph below, we have
$x$-intercept $(-1,0)$ and $y$-intercept $(0,1)$
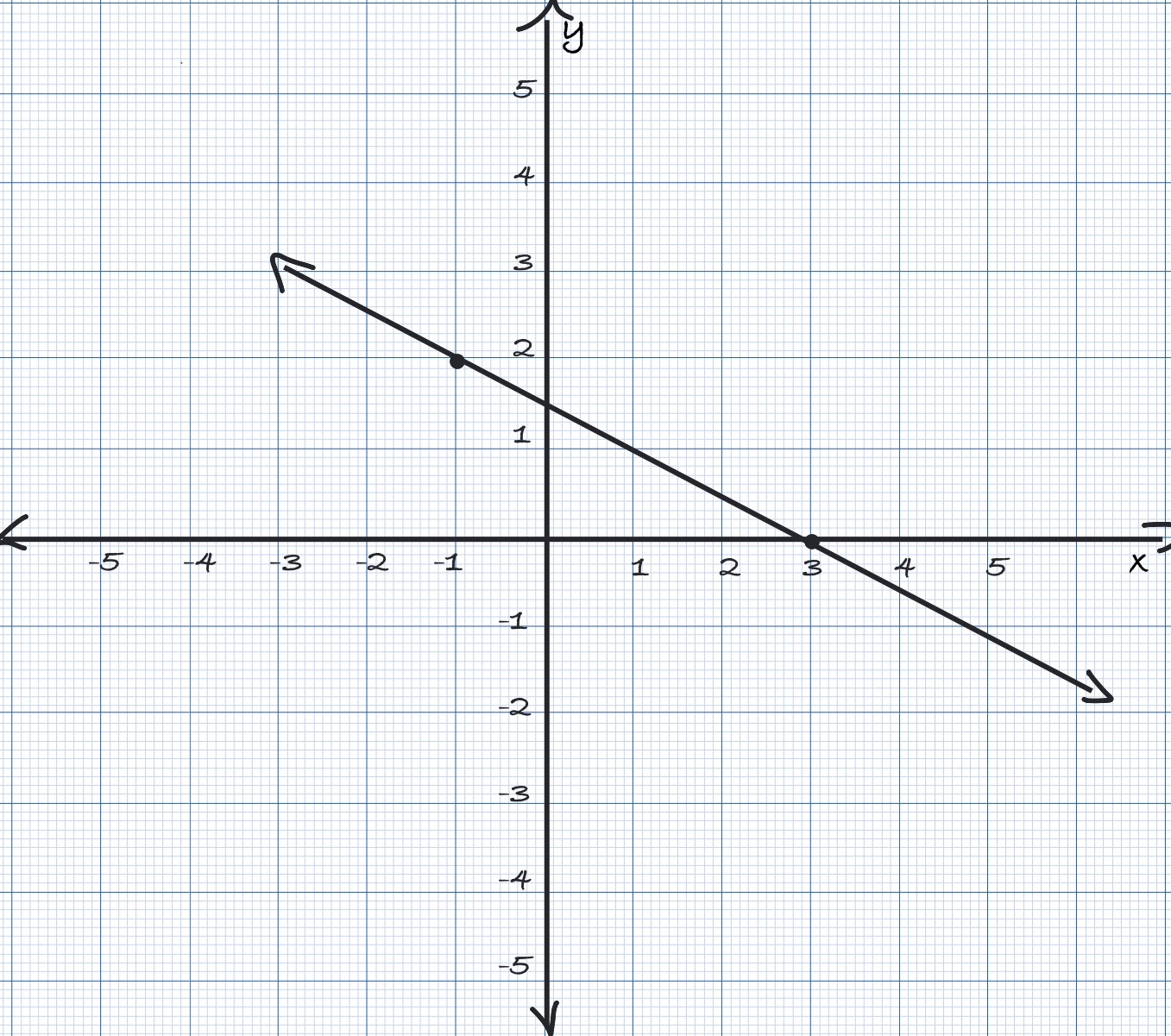
 $(ii)$ Slope is $\frac{0-2}{3+1} = \frac{-2}{4} = -\frac{1}{2}$. From the graph below, we note that $x$-intercept is $(3,0)$ and
$y$-intercept is $(0,\frac{3}{2})$.
$(ii)$ Slope is $\frac{0-2}{3+1} = \frac{-2}{4} = -\frac{1}{2}$. From the graph below, we note that $x$-intercept is $(3,0)$ and
$y$-intercept is $(0,\frac{3}{2})$.
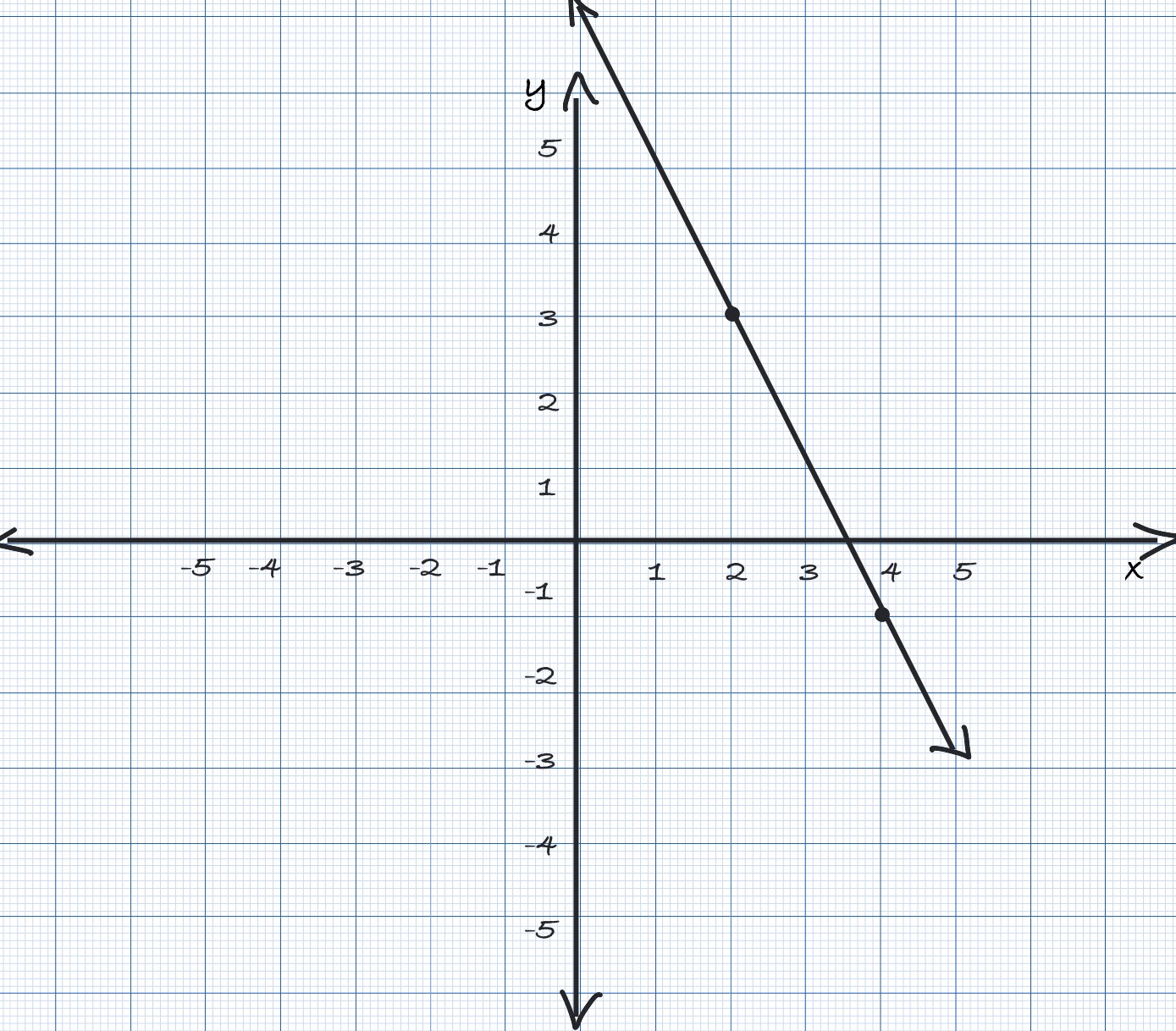
 $iii$ Slope is $ \frac{-1-3}{4-2} = \frac{-2}{2} = -1$. From the graph below, we note that $x$-intercept is $(3,0)$ and
$y$-intercept is $(0,3)$.
$iii$ Slope is $ \frac{-1-3}{4-2} = \frac{-2}{2} = -1$. From the graph below, we note that $x$-intercept is $(3,0)$ and
$y$-intercept is $(0,3)$.
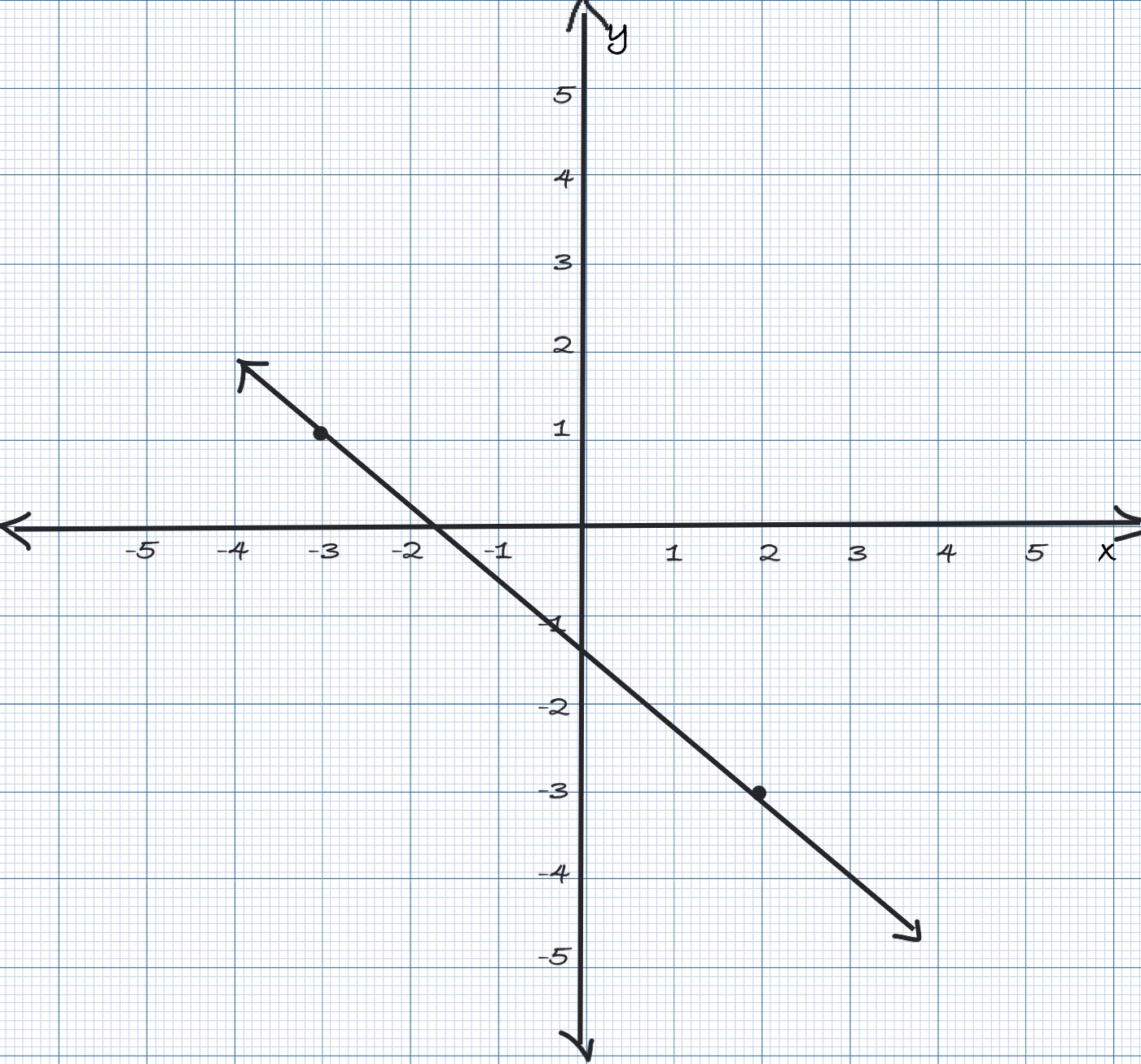
 $(iv)$ Slope is $\frac{-3-1}P{2+3} = -\frac{4}{5}$. From the graph below, we note that $x$- intercept is $(-\frac{7}{4},0)$ and
$y$-intercept is $(0,-\frac{7}{5})$
$(iv)$ Slope is $\frac{-3-1}P{2+3} = -\frac{4}{5}$. From the graph below, we note that $x$- intercept is $(-\frac{7}{4},0)$ and
$y$-intercept is $(0,-\frac{7}{5})$
If we write the numerator in the slope formula $y_2 - y_1$ as $\Delta y$ and the denominator $x_2 - x_1$ as $\Delta x$, then the slope formula can be written as $m = \frac{\Delta y}{\Delta x}$. For in this reason the slope is also referred to as rate of change of the function $y=f(x)$ with respect to $x$.The following aspects/properties of linear functions are worth recalling. These were discussed in detail in Chapter 1.
Write the equation, in slope-intercept form, of the linear function such that $f(-1)=2$ and $f(3)=-2$
Solution: Given information suggest the two points $(-1,2)$ and $(3,-2)$ on the line. Slope of the function:$$\frac{-2-2}{3+1} = \frac{-4}{4} = -1$$. We can write the equation of the line in point-slope form by taking the point $(-1,2)$: \begin{eqnarray} y -2 &=& -1(x +1)\\ y-2 &=& -x-1\\ y &=& -x -1 + 2\\ y &=& -x + 1\\ \end{eqnarray}
Find the equation, in general form, of a line parallel to the line $x + 3y = 6$ and passing through the point $(1, -2)$.
Solution:Slope of the given line: \begin{eqnarray} x+3y &=& 6\\3y &=& -x + 6\\ y &=& -\frac{1}{3}x + 2\\ \end{eqnarray} Slope of the required line, parallel to the given line: $$m = -\frac{1}{3}$$ Equation in point-slope form, simplified to general form: \begin{eqnarray} y + 2 &=& -\frac{1}{3}(x-1)\\ 3(y + 2) &=& -x + 1\\ 3y + 6 &=& -x +1\\ x + 3y &=& -5\\ \end{eqnarray}
Find the equation of the line, in slope-intercept form, that is perpendicular to the line $x-2y=4$ and passing through $(0,3)$.
Solution: Write the equation of the given line in slope-intercept form: \begin{eqnarray} x-2y &=& 4\\ -2y &=& -x+4\\ y &=& \frac{1}{2}x - 2\\ \end{eqnarray} slope of the given line: $$m_1 = \frac{1}{2}$$ So, slope of the required line, perpendicular to the given line: $$m = -2$$ The required line passes through the point $(0,3)$. As this point lies on the $y$-axis, the $y$- intercept of this line is $3$. We write the equation of the required line as $$ y = -2x+3$$.
Find the equation, in slope-intercept form, of the line that has $x$- and $y$- intercepts $(3,0)$ and$(0,-2)$ respectively. Graph this function.
Solution: As the two intercepts are given, we shall first find the equation in two-intercepts form: \begin{eqnarray} \frac{x}{3} + \frac{y}{-2} &=& 1\\ \frac{x}{3} - \frac{y}{2} &=& 1\\ \end{eqnarray} Rewrite this in slope-intercept form: \begin{eqnarray} \frac{x}{3} - \frac{y}{2} &=& 1\\ 2x - 3y &=& 6\\ -3y &=& -2x + 6\\ y &=& \frac{2}{3}x - 2\\ \end{eqnarray}
As already seen, the standard form of a quadratic function is $f(x) = ax^2 + bx + c$, where $a$, $b$, and $c$ are real numbers and $a \neq 0$. This is a function having the quadratic power function as its leading term. Because of this fact, we can graph a quadratic function using transformations by rewriting the standard form appropriately, using "completing the square" process: \begin{eqnarray} f(x) &=& ax^2 + bx + c\\ &=& a\left(x^2 + \frac{b}{a}x + \frac{c}{a}\right)\\ &=& a\left(x^2 + 2 \left(\frac{b}{2a}\right)x + \left(\frac{b}{2a}\right)^2 \right)^2 +\frac{c}{a} - \left(\frac{b}{2a}\right)^2 \\ &=& a\left(x+\frac{b}{2a}\right)^2 + \left(\frac{c}{a} - \frac{b^2}{4a^2}\right)\\ \end{eqnarray} Now, if we let $-\frac{b}{2a} = h$ and $\frac{c}{a} - \frac{b^2}{4a^2} = k$, we can simplify this equation as $a(x-h)^2 + k$. This is called the vertex form of the quadratic equation. Given the standard form, we can easily compute the constants $h$ and $k$ using the formulas $h = -\frac{b}{2a}$ and $k = f(h)$ or $k = \frac{c}{a} - \frac{b^2}{4a^2}$. We can use the formula $k=c-ah^2$ also to determine the value of $k$. We can graph the quadratic function using following transformations:
Describe how to transform the graph of the power function $f(x)=x^2$ to get the graph of the function $4-3(x-1)^2$. Sketch the graph of this function.
Solution:$(i)$ Stretch vertically by a scale factor of 3 units to get $3f(x) = 3x^2$; $(ii)$ Translate horizontally to the right by 1 unit to get $3(f(x-1)^2 = 3(x-1)^2$; $(iii)$ Reflect on $x$-axis to get $-3f(x-1) = -3(x-1)^2$; $(iv)$ Translate vertically up by 4 units to get $-3f(x-1)+4 = 4-3(x-1)^2$. In the graph below, the pink curve shows step $(ii)$, blue curve shows step $iii)$,and the black curve is the final graph of the function.
Graph of a quadratic function is $U$ shaped, and it opens up if $a \gt 0$ and opens down if $a \lt 0$. For example, let us see the graph of the function $f(x) = x^2 - 2x - 1$:
The leading coefficient is $1$, which is positive. The shape of the graph opens upwards. Also we observe some more properties of the graph of the function, which can be generalized to the graph of any quadratic function.
Generally, the graph of a quadratic function, which is a parabola, has following properties:
Find the vertex, axis of symmetry, intercepts, maximum/minimum point, and range of the function $f(x) = 3(x+2)^2-6$
Solution: Vertex $(h,k) = (-2,-6)$; Axis of symmetry: $x = -2$; To find $y$- intercept, set $x = 0$ and solve: \begin{eqnarray} f(x) &=& 3(0+2)^2-6\\ &=& 3(4)-6\\ &=& 6\\ \end{eqnarray} To find the $x$- intercept, set $f(x)=0$ and solve: \begin{eqnarray} 3(x+2)^2 - 6 &=& 0\\ 3(x+2)^2 &=& 6\\ (x+2)^2 &=& 2\\ x+2 &=& \pm \sqrt{2}\\ x &=& -2 \pm \sqrt{2}\\ \end{eqnarray} So, the graph has $y$-intercept $(0,6)$ and $x$- intercepts $(-3.5,0)$ and $(-0.5,0)$ approximately; As the leading coefficient is positive, the graph opens up. So, it has a minimum point at the vertex $(-2,-6)$; Range of the graph is $y \in [-6, \infty)$.
Write the vertex form of the function $f(x) = -2x^2 +4x-5$ and determine the vertex, axis of symmetry, minimum/maximum value, intercepts, and range of the function. Verify your answers by graphing this function.
Solution:From the given function, we have $a = -2$, $b = 4$, and $c = -5$. From the formulas, we get the $x$-coordinate of the vertex: \begin{eqnarray} h &=& -\frac{b}{2a}\\ &=& -\frac{4}{-4}\\ &=& 1\\ \end{eqnarray} The $y$- coordinate of the vertex can be obtained by substituting the value of $h$ in the function or using the formula. Substituting $x = 1$ in the function, \begin{eqnarray} y &=& -2(1)^2 + 4(1) -5\\ &=& -2+4-5\\ &=& -3\\ \end{eqnarray} So, we get the vertex of the graph as $(1,-3)$. Axis of symmetry is $x = 1$. As the leading coefficient $a = -2$, which is negative, the parabola opens down. This makes the vertex the maximum point. So, maximum value of the function is $-3$ that occurs at $x = 1$. Range of the function is all real numbers $y \in (-\infty,k]$. The curve does not intersect or touch the $x$ axis as the equation $-2x^2+4x-5=0$ has no real solutions. $y$- intercept of the graph is $(0,-5)$. These are verified by the graph shown below:
An alternate way of graphing a quadratic function is to use its symmetric property, shape, vertex, and the intercepts, if possible, or one additional point on the graph.
Sketch the graph of a quadratic function that opens down, having the vertex at the point $(-1,1)$, and passes through the point $(1,-1)$.
Solution:First, plot the vertex point and the given point on a coordinate system. As the graph opens down, vertex should be the maximum point. Note that
the $x$- coordinate of the given point is $2$ more than the $x$-coordinate of the vertex. Due to symmetry, there should be another point on the graph whose $x$-
coordinate is $2$ less than that of the vertex, with the same $y$- coordinate - the point $(-3, -1)$. Plot this point also, and join these three points in freehand curve, keeping
in mind the fact the the graph has a maximum at the vertex.
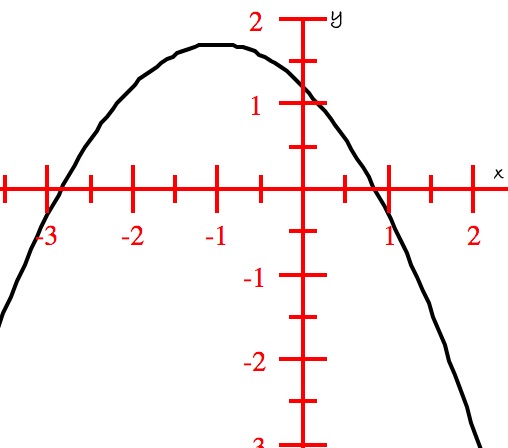
Rewrite the quadratic function $f(x) = 8+2x-x^2$ in vertex form using the 'completing the square method'. Then, describe the graph of this function.
Solution: Vertex form: \begin{eqnarray} f(x) &=& 8 + 2x - x^2\\ &=& (2x-x^2) + 8\\ &=& -1(x^2-2x) + 8)\\
&=& -1(x^2-2x+1) + 8 +1\\ &=& -1(x-1)^2 + 9\\ \end{eqnarray} So,the vertex form of this function is $f(x) = -1(x-1)^2+9$.
$(i)$ As $a \lt 0$, the graph opens down. $(ii)$ Vertex is $(1,9)$. $(iii)$ Equation of axis of symmetry: $x = 1$; $(iv)$ Maximum value is
9, that occurs at $x = 1$; $(v)$ $x$- intercepts are obtained by setting $y = 0$ and solving for $x$: \begin{eqnarray} -(x-1)^2 +9 &=& 0\\
(x-1)^2 &=& 9\\ x-1 &=& \pm \sqrt{9}\\ x-1 &=& \pm 3\\ x &=& 4 \quad or \quad -2\\ \end{eqnarray} So, $x$- intercepts are $(-2,0)$ and $(4,0)$;
$y$- intercept is obtained by setting $x = 0$ and solving for $y$: \begin{eqnarray} y &=& -1((-1)^2+9\\ &=& -1+9 &=& 8\\ \end{eqnarray} So, $y$-intercept is
$(0,8)$; $(vi)$ Range of the function is all real values such that $y \in (-\infty,9]$. The graph shown below confirms all the properties of the functions
as described above.
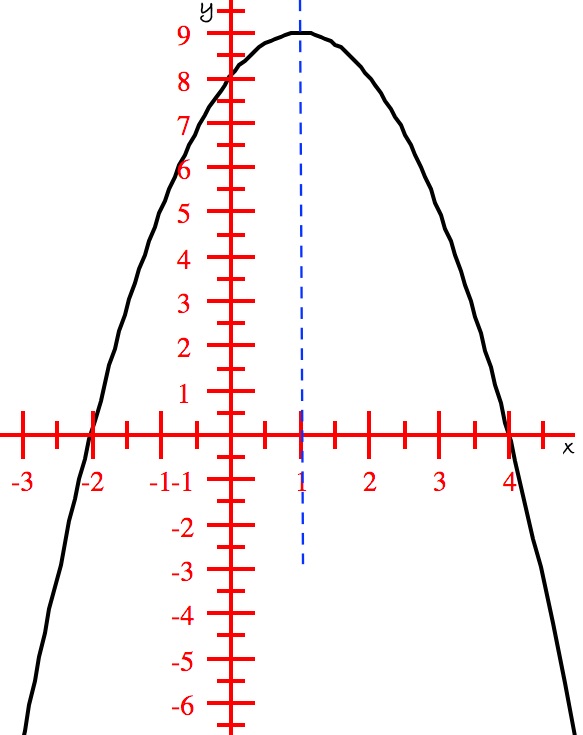
Rewrite the function $f(x) = -2(x+1)^2+4$ in general form. Determine the intercepts, if any, vertex, domain, and range. Also, list the intervals on which the function is increasing or decreasing. Sketch a graph of this function and verify your answers.
Solution:General form of the function: \begin{eqnarray} f(x) &=& -2(x+1)^2 + 4\\ &=& -2(x^2 + 2x + 1) + 4\\ &=&-2x^2 - 4x -2 + 4\\
&=& -2x^2 - 4x + 2\\ \end{eqnarray} So, the general form is $f(x) = -2x^2-4x+2$; Setting $f(x)=0$ and solving for $x$,we get the $x$- intercepts as $(-2.5,0)$
and $(0.5,0)$ approximately. Setting $x=0$ and solving for $y$, we get the $y$- intercept $(0,2)$; Vertex is $(1,4)$;
Domain is the set of real numbers $x \in (-\infty,\infty)$ and range is the set of real numbers $y \in (-\infty, 4]$; The graph increases on the interval
$(-\infty,4)$ and decreases on the interval $(4, \infty)$.
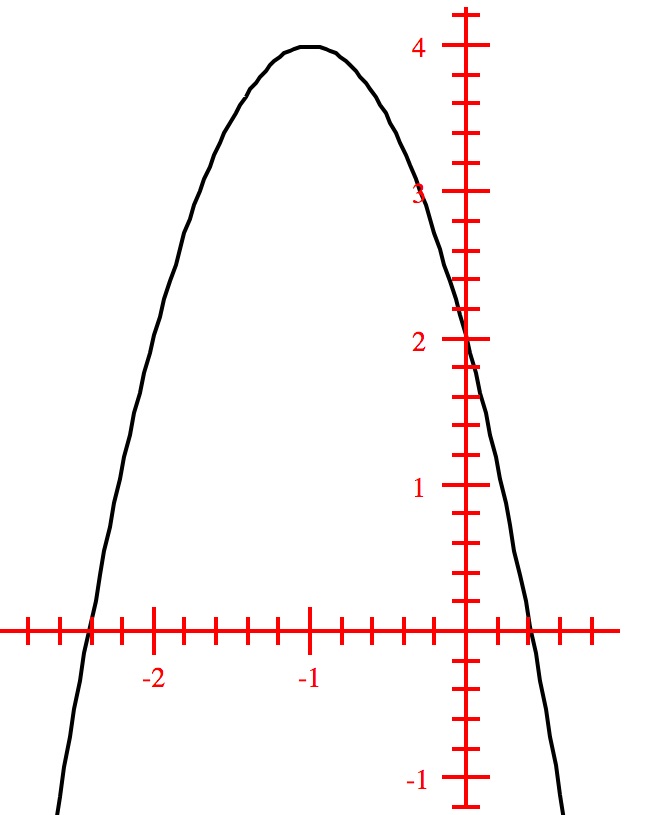
Determine the vertex, axis, domain, and range of the function $g(x) = x^2-0.1x-1$. List the intervals on which the graph increases or decreases.
Solution: As the function is in general form, we shall find the vertex using the vertex formulas: \begin{eqnarray} h &=& \frac{-b}{2a}\\
&=& \frac{0.1}{2}\\ &=& 0.05\\ k &=& (0.05)^2 -0,1(0.05)-1\\ &=& 0.0025 -0.005-1\\ &=& 1.0025\\ \end{eqnarray} So, the vertex is $(0.05,-1.0025)$;
Axis of symmetry is $x = 0.05$; Domain is the set of all real numbers $x \in (-\infty, \infty)$ and range is the set of all real numbers $y \in [-1.0025,\infty)$;
The graph decreases on the interval $(-\infty,0.05)$ and then increases on the interval $(0.05, \infty)$.
$4x+3y=2$
$y=-x+4$
$y=-5x+3$
$y=2x+3$
$y=2x-7$
$y=4x+6$
$(i)$ Translate horizontally to the left by 2 units; $(ii)$ Stretch vertically by a scale factor of 3 units; $(iii)$ Translate vertically down by 4 units.
$(i)$ Translate horizontally 1 unit to the right; $(ii)$ Stretch vertically by a scale factor of 2; $(iii)$ Reflect on $x$-axis; $(iv)$ Translate vertically up by 6 units.
Vertex: $(2,5)$; Axis of symmetry: $x=2$; Range: all real numbers $y \in -\infty, 5]$.
Vertex: $\left(-\frac{3}{2}, \frac{5}{2}\right)$; Axis of symmetry: $x = -\frac{3}{2}$; Range: all real numbers $y \in \left[\frac{5}{2}, \infty \right)$.
$f(x)=3\left(x+\frac{5}{6}\right)^2+\frac{23}{12}$; Shape: opens up: Vertex: $\left(-\frac{5}{6},\frac{23}{12}\right)$; Axis: $x=-\frac{5}{6}$; Range: all real values $y \in \left[\frac{23}{12}, \infty\right]$; minimum value of $\frac{23}{12}$ occurs at $x=-\frac{5}{6}$.
$f(x)=-(x+3)^2+19$; Shape: Opens down; Vertex: $(-3,19)$; Axis: $x=-3$; Range: all real numbers $y \in (-\infty, 19]$; maximum value is $19$, occurs at $x=-3$.
$f(x) = 2(x-1)^2+3$
$x$-intercept: $\left(\frac{4}{3},0\right)$; $y$-intercept: $\left(0,\frac{2}{3}\right)$; slope: $-\frac{1}{2}$
$y=\sqrt{2}x-3$
$y=-\frac{3}{4}x+\frac{5}{4}$
$-2x+3y=-4$
$-2x^2-8x-5$; No $x$- intercepts; $y$-intercept: $(0,-5)$; Range: all real numbers $y \in (-\infty,-5]$ Maximum point: $(-2,3)$
.Vertex: $(3,-5)$; axis of symmetry: $x=3$; Range: $[-5,\infty)$.
$-2x+y=3$
$3x+y=6$
Opens downwards: Vertex: $\left(\frac{5}{6}, \frac{61}{9}\right)$
Opens upwards; Vertex: $(1,-9)$; Decreases on the interval $(-infty,1)$ and increases on the interval $ (1,\infty)$
Domain: all real number $x \in [0,15]$; Range: all real numbers $y \in [-56,72]$; Vertex: $(7,72)$; axis: $x=7$; Maximum value $72$ at $x=7$.
$f(x)=2 \left(x+\frac{1}{4}\right)^2 - \frac{25}{8}$; Decreases on the interval $\left(-\infty, \frac{1}{4}\right]$ and increases on the interval $\left[\frac{1}{4}, \infty \right)$.
$f(x)=(x+1)^2-4$
$f(x)=2x^2$
$f(x)=-(x+2)^2$