Precalculus

Solve the inequality grtaphically: $x^2-x-2 \gt 0$

Solution:

From the graph we see that the portion of the graph above the $x$-axis is from $(-\infty, -1)$ and $(2, \infty)$.
So,the solution set is the open intervals $(-\infty, -1)$ and $(2, \infty)$.

To solve the above inequality algebraically:

1. Step 1: Solve the corresponding equation : \begin{array} (x^2-x-2 &=& 0\\ (x-2)(x+1) &=& 0\\ x &=& 2 &or& x &=& -1\\ \end{array}
2. Step 2. The solution set $\{-1,2\}$ are called the critical points for the inequality. Partition the $x$-axis into three open intervals $(-\infty, -1)$, $(-1, 2)$, and $(2, \infty)$.
3. Step 3: Give test value in each of these intervals and determine the sign of the left side of the inequality.
4. Step 4: As the inequality implies all real numbers that make the left side expression greater than zero, select the intervals that give positive values.

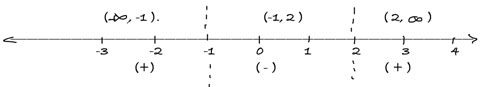
The above solution confirms the graphical solution that we got earlier.

Solve the inequality $6x^2-13x+6 \leq 0$

Solution:

Solving graphically:

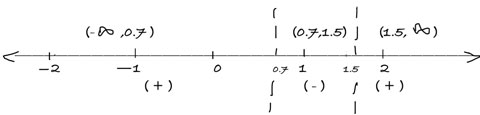
From the graph, we see that the critical points ($x$ intercepts) are $x=0.7$ and $x=1.5$ approximately. The portion below the $x$-axis is between these two points.
So,the solution set is $[0.7, 1.5]$. Solution set is a closed interval because the end points 0.7 and 1.5 are included in the solution.
To solve this algebraically, we first find the critical points by solving the corresponding equation: \begin{eqnarray} (6x^2-13x+6 &=& 0\\ 6x^2-9x-4x+6 &=& 0\\ 3x(2x-3)-2(2x-3) &=& 0\\ (2x-3)(3x-2) &=& 0\\ x &=& \frac{3}{2} &or& x &=& \frac{2}{3}\\ \end{eqnarray}
Dividing the number line into three intervals based on these two critical points and checking the sign of the quadratic expression on the left side, we conclude that the solution set is $[0.7, 1.5]$

The number line above confirms the graphical solution.

Solve the inequality $3x^3-12x+2 \geq 0$ graphically.

Solution:
Graph the equation $y=3x^3-12x+2$

Note that the graph is above the $x$-axis in the intervals $-2.1\lt x \lt 0.2$ and $1.9 \lt x \lt \infty$
So,the solution set is $[-2.1,0.2] \cup [1.9, \infty)$

Solve $x^3-x \lt 0$ algebraically.

Solution:
First, find the critical points by solving the corresponding equation $x^3-x=0$: \begin{eqnarray} x^3-x &=& 0\\ x(x^2-1) &=& 0\\ x(x+1)(x-1) &=& 0\\ x &=& 0 &or& x &=& 1 &or& x &=& -1\\ \end{eqnarray}
So, critical points are $x=0, 1,-1$.
Now, mark these points on the number line and partition the number line into four intervals.Then, check the sign of $x^3-x$ in each interval:

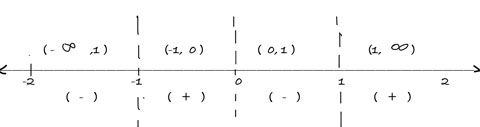
We find that this expression is negative for the intervals $(-\infty, -1)$ and $(0,1)$.
So,the solution set is $(-\infty,-1) \cup (0,1)$