Dr. Lalitha Subramanian
About the Author

Aksharam
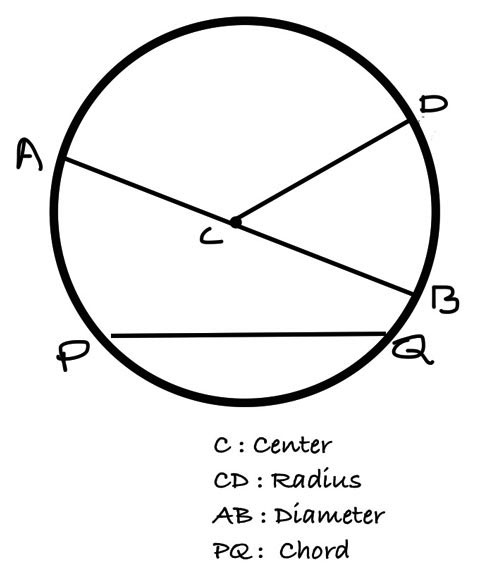
A circle is the locus of a point that moves such that it is always at a fixed distance from a fixed point in a plane.
Another way of defining a circle is the set of all points that are equidistant from a fixed point in a plane.
The fixed point is called the center of the circle and the fixed distance is called the radius of the circle.
A segment joining two points on the circle is called a chord of the circle.
A chord of the circle that passes through the center is called the diameter of the circle. A diameter is the longest chord of the circle. Length of the diameter is twice the radius.
Using the definition of the circle, we can write the equation of the circle as $$(x-h)^2+(y-k)^2=r^2$$ where $(h,k)$ is the center of the circle and $r$ is the radius. This form of equation of the circle is called Standard Form .
Find an equation of a circle with center $(-2,1)$ and radius $3$. Graph the circle.
Solution: Substitute $h=-2$, $k=1$,and $r=3$ in the equation, we get $$(x+2)^2+(y-1)^2=9$$
Find the coordinates of the center and the length of the radius of the circle whose equation is $(x+1)^2+(y-3)^2=4$ Then graph the circle.
Solution: Comparing the given equation with the standard form,we get the center as $(-1,3)$ and radius as $2$
We get the General Form of the equation of the circle by expanding the square terms and simplifying: \begin{eqnarray} (x-h)^2+(y-k)^2 &=& r^2\\ (x^2-2hx+h^2)+(y^2-2ky+k^2) &=& r^2\\ x^2+y^2-2hx-2ky+h^2+k^2-r^2 &=& 0\\ \end{eqnarray}
Find the general form of the equation of a circle whose center is $(2,-3)$ and radius is $4$.
Solution: the equation in standard form is \begin{eqnarray} (x-2)^2+(y+3)^2=4^2\\ \end{eqnarray} Expanding and rearranging gives \begin{eqnarray} x^2-4x+4+y^2+6x+9-16 &=& 0\\ x^2+y^2-4x+6y-3 &=& 0 \end{eqnarray}
Find the center and radius of the circle whose equation is $x^2+y^2-6x-4y+4=0$.
Solution: Here we need to work backward and bring the general form to standard form. This is achieved in the following way: First, bring the constant term to the right side, and group the variables: \begin{eqnarray} x^2-6x+y^2-4y &=& -4\\ \end{eqnarray}
Then, Use completing the square process: \begin{eqnarray} (x^2-6x+3^2)+(y^2-4y+2^2) &=& -4+3^2+2^2\\ \end{eqnarray} Simplifying, \begin{eqnarray} (x-3)^2+(y-2)^2 &=& 9\\ \end{eqnarray} This is the standard form. From this, we see that the center is $(3, 2)$ and radius is $3$
Find the center and radius of the circle whose equation is $x^2+y^2+10x-4y+21=0$.
Solution: Like the previous example, we need to work backward and bring the general form to standard form. \begin{eqnarray} x^2+10x+y^2-4y &=& -21\\ (x^2+10x+5^2)+(y^2-4y+2^2) &=& -21+25+4\\ (x+5)^2+(y-2)^2 &=& 8\\ \end{eqnarray} This is the standard form. From this, we see that the center is $(-5, 2)$ and radius is $2\sqrt{2}$
For problems (1) through (6), find the radius and the center of each circle and then graph the circle
Center $(0,0)$; Radius $5$
Center $(1,-2)$; Radius $2\sqrt{5}$
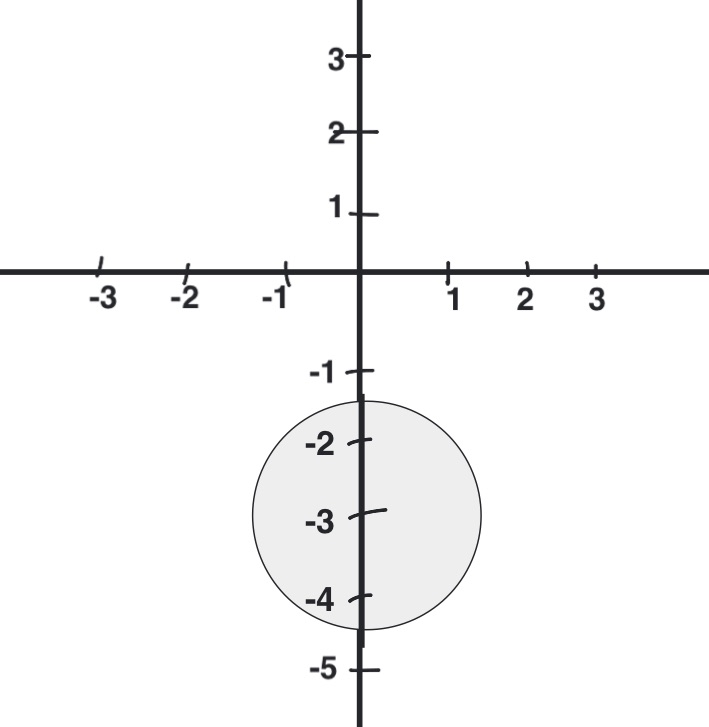
Center $(0,-3)$; Radius $\frac{2}{3}$
Center $(-1,0)$; Radius $3\sqrt{5}$
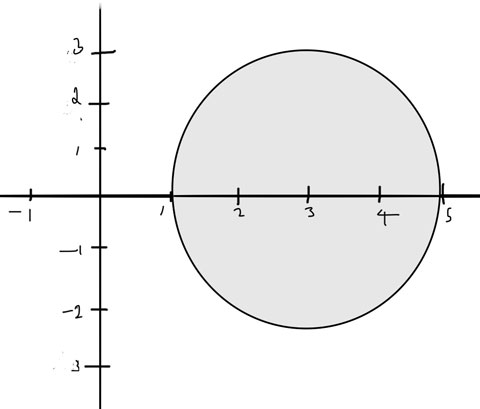
Center $(3,0)$; Radius $2$
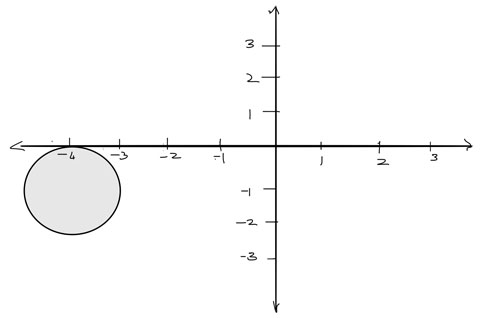
Center $(-4,-1)$; Radius $1$
For problems from (7) through (12), find the equation of the circle in standard form with the given information.
$(x-2)^2+y^2=25$
$(x-6)^2+(y-2)^2=3$
$(x+4)^2+(y+3)^2=100$
$(x+5)^2+(y-2)^2=\frac{4}{9}$
$(x-2)^2+(y-1)^2=10$
End points of the diameter is given. Diameter = $\sqrt{8}$=$2\sqrt{2}$. Radius=$\sqrt{2}$. Center of the circle is the midpoint of the diameter.Center is $(1,4)$. Hence the equation is $(x-1)^2+(y-4)^2=2$.
For problems (13) through (20), Find the equation of the circle in general form using the given information.
$x^2+y^2+2y=0$
$x^2+y^2+4x-2y-11=0$
$x^2+y^2-2x+4y=0$
$(x-5)^2+(y+3)^2=117$
Center is $(-5,-4)$ and diameter is $3$
$x^2+y^2=4$